Kreiseltheorie

Kreisel

Die Kreiseltheorie beschäftigt sich mit rotierenden Körpern, bei denen translatorische Bewegungen und Deformationen von untergeordneter Bedeutung sind. Körper, auf die diese Beschreibung zutrifft, werden in der Theorie zusammenfassend als Kreisel bezeichnet und beinhalten so verschiedene Objekte wie Spielzeugkreisel, Langgeschosse oder die Erde. Die Kreiselbewegungen sind für Mathematik, Physik und Ingenieurwesen – somit für Theorie und Praxis – gleichermaßen attraktiv. Ziel der Theorie ist es, Anwendungen auf eine sichere Grundlage zu stellen. Die Ästhetik des Gegenstands und seine anfängliche mathematische Unnahbarkeit hatten der Kreiseltheorie den Ruf einer „mathematischen Nixe“ eingetragen. Heute ist das „Kreiselproblem“ bis hin zu Detailfragen ausgelotet.

Die Kreiseltheorie definiert Eigenschaften von Kreiseln (Massenmittelpunkt, Hauptträgheitsachsen, …), deren Kinematik (Winkelgeschwindigkeit, Euler-Winkel, …) und Kinetik (Drehimpuls, Euler’sche Kreiselgleichungen, …), leitet, auch mit dem Lagrange-Formalismus, Bewegungsfunktionen der Kreisel ab und gibt Methoden (Poinsotsche Konstruktion, Phasenraumportraits, …), diese anschaulich darzustellen.

Leonhard Euler begründete die (analytische) Kreiseltheorie mit den nach ihm benannten Kreiselgleichungen, die die Winkelbeschleunigungen mit den angreifenden Drehmomenten im körperfesten Bezugssystem verbinden. Die Kreiselgleichungen sind integrabel im kräftefreien Euler-Kreisel, im schweren symmetrischen Lagrange-Kreisel, im schweren, symmetrischen, inhomogenen Kowalewskaja-Kreisel und ansonsten nur in speziellen Kreiselbewegungen. In den integrablen Fällen hat die Winkelgeschwindigkeit wenigstens einen quasi periodischen Verlauf.

Anwendungen findet die Kreiseltheorie in der Eisenbahntechnik (Sinuslauf), der Stabilisierung von Schiffen (Schiffskreisel), Raumflugkörpern und Trägheitsnavigationssystemen sowie in der Astronomie und Ballistik.

Geschichte

Bis zu Eulers bahnbrechenden Arbeiten sind folgende Beiträge zu erwähnen:

Archimedes gab Grundsätze über den Schwerpunkt mehrerer Größen an und formulierte Bedingungen für das statische Momentengleichgewicht.
Johannes Kepler entdeckte 1609 die ersten beiden seiner drei Kepler’schen Gesetze, von denen das zweite eine Konsequenz der Drehimpulserhaltung ist.
Jakob I Bernoulli wandte 1703 den Drallsatz an – ohne ihn jedoch explizit zu formulieren – um das Oszillationszentrum eines Pendels zu finden, was er bereits auch in einem ersten, etwas unrichtigen Versuch 1686 tat.
Isaac Newton veröffentlichte 1687 seine Prinzipia mit seinen Newton’schen Gesetzen, insbesondere formulierte er die Impulsbilanz Kraft gleich Masse mal Beschleunigung.

Leonhard Euler entwickelte 1736 eine Theorie der Präzession und 1750 seine Kreiselgleichungen und konnte auch schon Lösungen für den kräftefreien Euler-Kreisel angeben. Joseph-Louis Lagrange leistete 1788 einen wichtigen Beitrag durch Lösung der Gleichungen für den schweren symmetrischen Kreisel. Carl Gustav Jacob Jacobi veröffentlichte 1829 seine Theorie der Jacobi'schen elliptischen Funktionen und der Theta-Funktionen, mit denen sich die Kreiselgleichungen lösen lassen. Sofia Kowalewskaja entdeckte 1888 den letzten durch Theta-Funktionen lösbaren Fall, den schweren, symmetrischen, inhomogenen Kowalewskaja-Kreisel, womit die analytische Kreiseltheorie zu einem gewissen Abschluss kam. Édouard Husson zeigte 1905 in seiner Dissertation, dass der Euler-, Lagrange- und Kowalewskaja-Kreisel die einzigen mit algebraischen Integralen lösbaren Fälle der Kreiselgleichungen sind. Darüber hinaus können nur spezielle Bewegungen integrabel sein.

Durch die Raumfahrt kamen neue Problemstellungen hinzu, wie beispielsweise

die Selbsterregung (im körperfesten System aufgebrachte Momente) zwecks Stabilisierung und Lageregelung, Stabilisierung (Raumfahrt),
die Bewegungen von Körpern mit veränderlichen Massen,
die Bewegungen starrer Körper mit Flüssigkeitsfüllung,
die Drehbewegungen in einem zentralen Schwerefeld oder
die Beeinflussung von Translations- und Rotationsbewegungen.

Die meisten Kreiselbewegungen sind nicht analytisch lösbar. Die sinnfällige graphische Darstellung ihres Verhaltens wurde erst mit dem Einsatz von Computern und numerischen Integrationsverfahren möglich und ist Anfang des 21ten Jahrhunderts Gegenstand der Forschung.

Eigenschaften der Kreisel und ihrer Bewegungen

Ein Kreisel im Sinn der Kreiseltheorie ist ein beliebig gestalteter starrer Körper, der in einem Inertialsystem in einem seiner Punkte, dem Fixpunkt, derart festgehalten wird, dass er sich um diesen Punkt noch irgendwie drehen kann. Diese Forderung stellt nur eine kleine Einschränkung dar, denn jede Starrkörperbewegung lässt sich in Rotation und Translation zerlegen. Sofern letztere (näherungsweise) gleichförmig ist, spielt sie für die Kreiselbewegung keine Rolle. Es werden also auch Planeten oder der Spielzeugkreisel von der Kreiseltheorie betrachtet auch wenn dort kein Punkt fixiert ist.

Jeder Starrkörper hat drei ausgezeichnete Achsen, die Hauptträgheitsachsen, die paarweise zueinander senkrecht sind oder orthogonalisierbar sind. Diese Achsen bilden eine Orthonormalbasis, die kurz Hauptachsensystem genannt wird. Bezüglich dieser Achsen gleichen sich Fliehkräfte bei der Drehung genau aus und der Kreisel kann sich gleichförmig frei um sie drehen. Das Maß für den Widerstand des Kreisels gegen Bewegungsänderungen sind seine Trägheitsmomente, die bei diesen Achsen Hauptträgheitsmomente Θ_1,2,3 genannt werden. Häufig werden die Hauptträgheitsmomente Θ_1,2,3 auch mit A, B und C und die Hauptachsen 1, 2, 3 mit ξ, η und ζ bezeichnet.

Der unsymmetrische Kreisel besitzt drei verschiedene Hauptträgheitsmomente während beim symmetrischen Kreisel zwei Hauptträgheitsmomente überein stimmen. Ist das dritte Hauptträgheitsmoment größer als die beiden anderen, dann wird der symmetrische Kreisel abgeplattet oder oblat genannt, andernfalls gestreckt oder prolat. Eine anschauliche Vorstellung von der Bewegung eines symmetrischen Kreisels vermittelt der Durchstoßpunkt der Figurenachse (Symmetrieachse) durch die Einheitskugel. Dieser Durchstoßpunkt wird Locus der Figurenachse genannt (englisch Apex of the top). Von den auf den Kreisel einwirkenden äußeren Kräften ist die Schwerkraft die bei weitem wichtigste. Daher werden kräftefreie (eigentlich momentenfreie) und schwere Kreisel unterschieden, je nachdem ob der Schwerpunkt des Kreisels im Stützpunkt liegt oder nicht. Die beim symmetrischen Kreisel auf der Figurenachse und der Lotlinie senkrechte Achse wird Knotenlinie genannt. Beim schnellen Kreisel dominiert seine Rotationsenergie über andere Energieformen.

Die Hauptträgheitsmomente sind die Eigenwerte und die Hauptträgheitsachsen ${\hat {e}}_{1,2,3}$ die dazugehörigen Eigenvektoren des Trägheitstensors, der beim rotierenden Kreisel eine vergleichbare Rolle übernimmt wie die Masse bei der Translation. In der Kreiseltheorie wird er zumeist in der Hauptachsendarstellung verwendet und kann dort mit einer Diagonalmatrix identifiziert werden. Der Trägheitstensor bildet die Winkelgeschwindigkeit auf den Drehimpuls ab.

Drehgeschwindigkeit und Drehimpuls

→ Hauptartikel: Energieellipsoid

Abb. 1: Schnitt durch ein Energieellipsoid entlang zweier Hauptachsen, mit den Hauptträgheitsmomenten θ₁ und θ₂

Die Winkelgeschwindigkeit lässt sich kompakt als Vektor ${\vec {\omega }}$ ausdrücken: Seine Richtung definiert die Drehachse und sein Betrag die Drehgeschwindigkeit um diese Achse. Gleiches gilt für den Drehimpuls ${\vec {L}}$ , der ein Maß für den Schwung des Kreisels ist und der ebenfalls Richtung und Betrag besitzt.

Die Dynamik des Kreisels lässt sich mit dem Drehimpuls ähnlich der Dynamik des Massenpunkts formulieren:

Der kräftefreie Kreisel bewegt sich so, dass sein Drehimpuls nach Betrag und Richtung konstant bleibt (so wie sich ein kräftefreier Massenpunkt gleichförmig bewegt).
Unter dem Einfluss von Drehmomenten bewegt sich der Kreisel derart, dass die Änderungsgeschwindigkeit des Drehimpulsvektors nach Richtung und Betrag gleich dem angreifenden Moment ist (so wie die Beschleunigung des Massenpunkts in Richtung einer angreifenden Kraft erfolgt). Das ist die Aussage des Drallsatzes, auf den unten näher eingegangen wird.

Wird der Drehimpuls im körperfesten Hauptachsensystem ausgedrückt, dann sind die Komponenten in Richtung der Hauptachsen mit den größten Hauptträgheitsmomenten gegenüber den entsprechenden Drehgeschwindigkeiten betont. Die Richtung des Drehimpulses liegt daher immer irgendwo zwischen der Drehachse und den Hauptachsen mit den größten Hauptträgheitsmomenten.

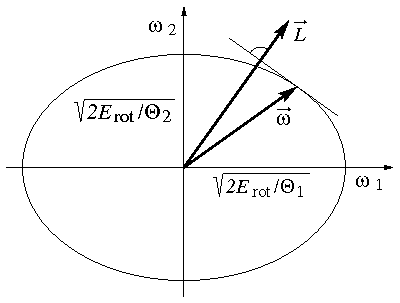
In Abb. 1 ist ein Schnitt durch ein Energieellipsoid zu sehen, das die Menge aller Winkelgeschwindigkeiten ist, die bei einem gegebenen Kreisel zur selben Rotationsenergie E_rot führen. Die Richtung des Drehimpulses steht immer senkrecht auf dem Energieellipsoid in dem Punkt, wo die aktuelle Winkelgeschwindigkeit dieses berührt. Die Länge der Halbachsen des Ellipsoids sind umgekehrt proportional zu den Hauptträgheitsmomenten: Das Hauptträgheitsmoment in horizontaler Richtung ist im Bild kleiner als das in vertikaler. Daher ist der Drehimpuls im Bild steiler ausgerichtet als die Winkelgeschwindigkeit. Nur bei Drehungen um eine der Hauptachsen sind Drehimpuls und Winkelgeschwindigkeit parallel. Liegt die Drehachse hingegen dazwischen, schließen sie einen spitzen Winkel ein und der ist umso spitzer, je näher die Winkelgeschwindigkeit an einer Hauptachse liegt.

Präzession und Nutation des symmetrischen Kreisels

→ Hauptartikel: Symmetrischer Kreisel

Abb. 2: Bewegungsform eines symmetrischen, prolaten, kräftefreien Kreisels

Betrachtet werden freie Bewegungen, bei denen die Drehachse ihre Richtung ändern kann.

Die Bewegungen des kräftefreien Kreisels werden in der Kreiseltheorie Nutation genannt und die fremderregten Präzession. Allerdings sind diese Bezeichnungsweisen nicht einheitlich. Arnold Sommerfeld beispielsweise nennt beim schweren symmetrischen Kreisel die periodische Änderung der Neigung der Figurenachse gegenüber der Lotlinie Nutation und die azimutale Drehung Präzession.

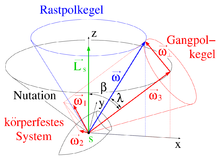
Rotiert der kräftefreie symmetrische Kreisel nicht um eine Hauptachse, dann fallen Drehimpuls und Winkelgeschwindigkeit nicht zusammen und die Figurenachse bewegt sich auf einem Kegel im Raum, siehe Abb. 2. Die Figurenachse ist körperfest.

Die Drehachse eines Kreisels ist nicht körperfest, sie kann sich also relativ zum Kreisel bewegen. Bei der Nutation des kräftefreien symmetrischen Kreisels beschreibt die Drehachse relativ zum Kreisel einen Kegel, den Gangpolkegel, mit konstantem Öffnungswinkel um die Figurenachse. Gleichzeitig überstreicht die Drehachse auch um die vom Drehimpuls gestellte Präzessionsachse einen Kegel, den Rastpolkegel, ebenfalls mit konstantem Öffnungswinkel, diesmal um die Präzessionsachse. Diese reguläre Präzession kann auch beim schweren symmetrischen Kreisel als Sonderfall auftreten.

Wenn der schwere Kreisel die speziellen Bedingungen der regulären Präzession nicht erfüllt, dann beschreibt der Locus der Figurenachse eine zykloidenähnliche Kurve, die sich auf die Präzession auswirkt. Diese überlagerte Bewegung wird nach einem der Astronomie entlehnten Wort ebenfalls Nutation genannt. Je größer das Verhältnis zwischen Rotations- und Lageenergie des Kreisels ist, desto kleiner wird der Radius der Zykloide, und das kann so weit gehen, dass die Rollkurve mit dem Auge nicht mehr als solche wahrnehmbar ist. Die Präzession sieht dann aus wie eine reguläre Präzession, ist aber keine, und wird pseudoreguläre Präzession genannt.

Drallsatz

→ Hauptartikel: Drallsatz

Abb. 3: Zur Regel vom gleichsinnigen Parallelismus

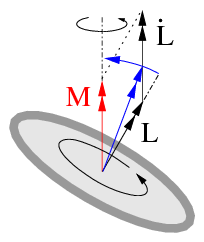
Das in der Kreiseltheorie wichtigste physikalische Gesetz ist der Drallsatz, der sich beim Kreisel als Regel vom gleichsinnigen Parallelismus ausdrückt, siehe Abb. 3.: Greift am Kreisel ein Drehmoment M an, dann versucht der Kreisel seine Drehbewegung, ausgedrückt durch den Drehimpuls L, dem Drehsinn des Moments gleichsinnig parallel auszurichten, was im Bild blau angedeutet ist. Aus diesem Grundsatz leiten sich viele Eigenschaften der Kreiselbewegungen ab. Wirkt auf den Kreisel beispielsweise eine Kraft, dann ist das von ihr ausgeübte Drehmoment senkrecht zu ihr und somit weicht ein rotierender Kreisel einer Kraft immer senkrecht zu ihrer Wirkungslinie aus. Das gilt jedoch nur für den Drehimpuls und nicht notwendigerweise auch für die Drehachse oder eine Symmetrieachse des Kreisels, siehe auch den Abschnitt Drallstabilisierung unten, wo die Figurenachse anfänglich vom Moment „mitgenommen“ wird.

Der Drallsatz besagt, dass um den Drehimpuls eines Kreisels zu verändern, ein Drehmoment angreifen muss. Ohne solche Momente bleibt der Drehimpuls in Betrag und Richtung erhalten. Die mathematische Formulierung lautet:

${\vec {M}}={\dot {\vec {L}}}$

Darin ist ${\vec {M}}$ das am Kreisel angreifende Drehmoment, ${\vec {L}}$ der Drehimpuls des Kreisels und ${\dot {{\vec L}}}$ seine zeitliche Änderung. Aus dem Drallsatz leiten sich auch die Euler’schen Kreiselgleichungen ab, mit denen die genaue rechnerische Behandlung der Kreiselbewegungen erfolgt, siehe unten. Der Drehimpuls und die Drehachse sind – wie oben berichtet – nur bei Drehungen um eine der Hauptachsen parallel. In den anderen Fällen gilt:

Bei konstantem Drehimpuls ändert sich bei freier Bewegung fortlaufend die Drehachse und der Kreisel taumelt oder „eiert“.
Wird die Drehachse festgehalten, dann ändert sich fortlaufend der Drehimpuls, mit den Konsequenzen:
- Die Halterungen der Drehachse müssen die dazu notwendigen Momente einbringen.
- Umgekehrt werden die Halterungen durch die Reaktionsmomente belastet und müssen diese abtragen.

Integration obiger Gleichung über die Zeit liefert

${\vec {L}}={\vec {L}}_{0}+\int {\vec {M}}\,\mathrm {d} t$

Das Integral ist der Drehstoß. Bei anfänglich ruhendem Körper liefert er einen Drehungszustand, der nicht notwendigerweise parallel zur Drehachse ist, worin sich die Anisotropie des starren Körpers gegenüber Drehbewegungen ausdrückt. Der unsymmetrische Kreisel ist doppelt anisotrop, der symmetrische einfach anisotrop und nur der Kugelkreisel isotrop.

Das Moment kann in eine Komponente M_L parallel zum Drehimpuls L₀ und eine Komponente M_P senkrecht dazu zerlegt werden. Erstere Komponente wirkt nur auf den Betrag des Drehimpulses nicht aber auf seine Richtung und letztere Komponente wirkt umgekehrt nicht auf den Betrag, sondern nur auf die Richtung. Ändert sich diese im Zeitintervall Δt um den Winkel Δα, dann entsteht:

$\omega _{\text{P}}=\lim _{\Delta t\to 0}{\frac {\Delta \alpha }{\Delta t}}={\frac {M_{\text{P}}}{L_{0}}}\quad {\text{oder}}\quad M_{\text{P}}=\omega _{\text{P}}\cdot L_{0}$

ein Zusammenhang, der bei der Quantifizierung der Drallstabilisierung unten ausgenutzt wird. Eine Verallgemeinerung in drei Dimensionen erklärt die Pseudoreguläre Präzession des Lagrange-Kreisels.

Kreiselwirkung

→ Hauptartikel: Gyroskopischer Effekt

Das auffälligste Merkmal von Kreiseln ist die des gyroskopischen Effekts oder der Kreiselwirkung. Wenn der Kreisel eine zusätzliche Drehung erfährt, dann gleicht sich die Eigendrehung des Kreisels der zusätzlichen Drehung an. Das ist die Folge der Kreiselwirkung, die also versucht nach der Regel des gleichsinnigen Parallelismus die Achse der Eigendrehung in Richtung und Orientierung mit der Achse der erzwungenen Drehung zur Deckung zu bringen.

Die Kreiselwirkung $\vec K$ ist eine d’Alembertsche Trägheitskraft und als solche ein einem angreifenden Moment ${\vec {M}}$ entgegengesetzt gleichgroßes Moment:

${\vec {K}}=-{\vec {M}}$

Moment und Kreiselwirkung befinden sich im dynamischen Gleichgewicht. Somit entspricht die Kreiselwirkung der negativen Drehimpulsänderung und ist gleich der Summe der Kreiselwirkungen der Euler- und (fiktiven, s.u.) Zentrifugalkräfte im Körper:

${\vec {K}}={\vec {K}}_{\mathrm {Euler} }+{\vec {K}}_{\text{Zentrifugal}}=-{\dot {\vec {L}}}$ .

In den Richtungen senkrecht zum angreifenden Moment neutralisieren sich die Kreiselwirkungen der Euler- und Zentrifugalkräfte und befinden sich dort somit untereinander im dynamischen Gleichgewicht. Die Euler-Kräfte sind Ausdruck von Winkelbeschleunigungen, die dort von den Zentrifugalkräften im Kreisel hervorgerufen werden. Umgekehrt führen die Winkelbeschleunigungen zur Änderung der Drehachse und Drehgeschwindigkeit, was die Zentrifugalkräfte beeinflusst. Folge dieses dynamischen Wechselspiels ist besagtes Taumeln und „Eiern“ des kräftefreien Kreisels.

Drallstabilisierung

Abb. 4: Schwungrad zur Erläuterung der Kreiselwirkung

Eine der technisch wertvollsten Eigenschaften von Kreiseln ist die Möglichkeit, mit ihnen Körper in ihrer räumlichen Ausrichtung zu stabilisieren. Dies wird, wie schon eingangs erwähnt, bei Schiffen, Raumflugkörpern und Geschossen ausgenutzt. Die Drallstabilisierung basiert auf Kreiselwirkungen.

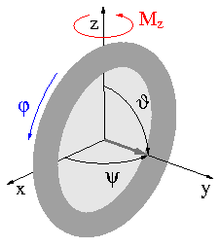
Um das zu erläutern, wird die Bewegung des Schwungrads in Abb. 4 betrachtet, wobei die Figurenachse (anfänglich in y-Richtung) frei ist, so dass sie ihre Richtung beliebig ändern kann. Auf dieses ansonsten kräftefreie Schwungrad wirke eine kurze Zeit in z-Richtung ein konstantes Moment M_z, das das Schwungrad in Drehung um z versetzt. Diese Drehung macht sich am ruhenden und rotierenden Schwungrad jedoch unterschiedlich bemerkbar:

Ruht das Schwungrad, dann beginnt es durch das Moment um z zu rotieren. Nachdem das Moment aufgehört hat zu wirken, verharrt das Schwungrad in der Drehung um z, es gibt keine Kreiselwirkung und der Drehwinkel ψ der Figurenachse um z nimmt monoton zu und ist unbeschränkt. Die Winkelgeschwindigkeit und der Drehimpuls haben nur eine Komponente und die weist in z-Richtung. Der Neigungswinkel ϑ zwischen Figurenachse und Momentenachse z bleibt unverändert.
Rotiert das Schwungrad anfänglich hinreichend schnell um die Figurenachse, dann zeigt sich ein anderes Bild. Zwar führt das Moment auch hier zu einer linearen Zunahme des Drehimpulses in z-Richtung, aber weil sich diese Komponente zum anfänglichen (als viel größer angenommenen) Drehimpuls in y-Richtung vektoriell addiert, der Drehimpuls also weiter vor allem in y-Richtung orientiert ist, und Drehimpuls und Winkelgeschwindigkeit einen spitzen Winkel einschließen (siehe oben), dreht das Schwungrad weiter vor allem um die y-Achse. Dadurch bleibt der Drehwinkel ψ der Figurenachse um z beschränkt. Nach der Regel des gleichsinnigen Parallelismus versucht der Kreisel seine Drehung dem angreifenden Moment anzugleichen, wodurch der Winkel ϑ abnimmt.

Ursache für den geringen Einfluss des Moments auf die Drehung des rotierenden Schwungrads um z sind Trägheitskräfte, die, wie im Folgenden geschildert, Gegenmomente aufbauen. Dabei wird der übliche Fall voraus gesetzt, dass das Schwungrad ein oblater Kreisel ist, sein Trägheitsmoment B um die Figurenachse also größer ist als die äquatorialen Trägheitsmomente A. Andernfalls wären die Kreiselwirkungen in x-Richtung umgekehrt orientiert. Anders als im Bild soll der Winkel ψ von der y-Achse aus zählen und es wird obiger Zusammenhang M = L ω benutzt, demgemäß ein Moment M zur Drehgeschwindigkeit ω eines zu ihm senkrechten Drehimpulses L führt.

Das kleine Moment M_z dreht das Schwungrad mit Drehimpuls L in y-Richtung zunächst (langsam) um die z-Achse und der Winkel ψ zur Figurenachse nimmt gemäß der Beschleunigungsgleichung $A{\ddot {\psi }}=M_{z}$ zu. Der Beschleunigungsterm $A{\ddot {\psi }}$ ist eine Kreiselwirkung in -z-Richtung, die sich aus Euler-Kräften speist.
So bekommt die Winkelgeschwindigkeit eine kleine Komponente in z-Richtung und die Neigung ϑ der Drehachse gegenüber der Vertikalen verringert sich entsprechend $A{\ddot {\vartheta }}=-L{\dot {\psi }}\rightarrow {\dot {\vartheta }}=-{\tfrac {L}{A}}\psi$ . Diese Winkelbeschleunigung um x zieht Euler-Kräfte nach sich, die in Summe eine Kreiselwirkung in -x-Richtung hervorbringen.
In gleicher Weise wie das Moment M_z die Kreiselwirkung in -x-Richtung hervorruft, so entsteht durch letztere eine weitere Kreiselwirkung $L{\dot {\vartheta }}=-{\tfrac {L^{2}}{A}}\psi$ in -z-Richtung, die der Beschleunigungsgleichung im ersten Schritt hinzu zu fügen ist: $A{\ddot {\psi }}=M_{z}-{\tfrac {L^{2}}{A}}\psi$ .
Ganz analog wie das Moment M_z eine entgegengesetzte Kreiselwirkung auslöst, besitzt auch die Kreiselwirkung in -x-Richtung eine Widersacherin in +x-Richtung, die sich aus den Zentrifugalkräften im Schwungrad speist und die ebenfalls zur Kreiselwirkung in -z-Richtung beiträgt.

Während sich die Kreiselwirkungen in -z-Richtung ( $A{\ddot {\psi }}$ und ${\tfrac {L^{2}}{A}}\psi$ ) genau zu M_z summieren, löschen sich die Kreiselwirkungen in x- und y-Richtung genau aus. Das Moment der Euler-Kräfte ist dort antiparallel zum Moment der Zentrifugalkräfte. Auf diese Weise bleiben die Drehimpulse in x- und y-Richtung gegenüber dem Anfangszustand unverändert.

Die im dritten Schritt erhaltene Gleichung für die Winkelbeschleunigung ${\ddot {\psi }}$ ist eine Schwingungsgleichung, weswegen die Figurenachse unter dem Moment in z-Richtung eine Schwingung um z ausführt. Mit dem konstanten Drehimpuls $L=B{\dot {\varphi }}$ in y-Richtung lautet die Schwingungsgleichung

${\frac {M_{z}}{A}}={\ddot {\psi }}+\left({\frac {B}{A}}{\dot {\varphi }}\right)^{2}\psi$

Darin ist φ der Drehwinkel um die Figurenachse. Die Eigenkreisfrequenz der Schwingung der Figurenachse um die z-Achse ist demnach proportional zum Verhältnis der Trägheitsmomente und zur Winkelgeschwindigkeit um die Figurenachse. Die Schwingungsgleichung ist eine Näherung, die nur bei kleiner Auslenkung ψ gültig ist. Aus ${\dot {\vartheta }}=-{\tfrac {L}{A}}\psi$ kann mit ψ auch ϑ berechnet werden.

Für die stabilisierende Kreiselwirkung ist dabei die freie Drehungsmöglichkeit der Figurenachse um die äquatorialen Achsen entscheidend. Wird die Drehachse durch Lager an die xy-Ebene gebunden, können die Momente der Trägheitskräfte nicht ihr Potenzial entfalten und es tritt keine Drallstabilisierung auf.

Kinematik von Kreiseln

Die Kinematik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die nicht von der Masse abhängen.

Eulersche Geschwindigkeitsgleichung

Die allgemeine Bewegung starrer Körper ist durch die eulersche Geschwindigkeitsgleichung

${\vec {v}}({\vec {x}},t)={\dot {\vec {b}}}(t)+{\vec {\omega }}(t)\times ({\vec {x}}-{\vec {b}}(t))$

gegeben. Sie gibt zur Zeit t für ein Partikel am Ort ${\vec {x}}$ die Geschwindigkeit ${\vec {v}}$ an, die sich aus der Bewegung eines Bezugspunkts ${\vec {b}}(t)$ und einer Drehung um ihn mit Winkelgeschwindigkeit ${\vec {\omega }}(t)$ zusammen setzt. Das Rechenzeichen „×“ bildet das Kreuzprodukt. In der Kreiseltheorie wird der Punkt ${\vec {b}}$ festgehalten und in den Ursprung eines Koordinatensystems gelegt, sodass ${\vec {b}}\equiv {\vec {0}}$ und die Geschwindigkeitsverteilung

${\vec {v}}({\vec {x}},t)={\vec {\omega }}(t)\times {\vec {x}}\,.$

gilt. Alle Partikel des Kreisels, die sich auf der Drehachse befinden (für die ist ${\vec {x}}\parallel {\vec {\omega }}$ ), ruhen solange sie das tun. Da die Drehachse nicht an die Partikel des Kreisels gebunden ist, kann sich die Drehachse relativ zum Kreisel bewegen, was eine wichtige Eigenschaft der Kreiselbewegung ist, die Präzession oder Nutation genannt wird, siehe oben.

Speziell für die rotierenden Hauptachsen berechnen sich die Raten

${\dot {\hat {e}}}_{i}:={\frac {\mathrm {d} }{\mathrm {d} t}}{\hat {e}}_{i}={\vec {v}}({\hat {e}}_{i},t)={\vec {\omega }}\times {\hat {e}}_{i}$

was analog auch für andere betraglich konstante körperfeste Vektoren gilt.

Bezugssysteme

→ Hauptartikel: Bezugssystem

In der Kreiseltheorie werden vor allem drei Bezugssysteme verwendet:

Im Inertialsystem, in dem der Stützpunkt ruht und der Kreisel rotiert, werden die Euler-Winkel definiert, die die Position des Kreisels, also die Orientierung seiner Hauptachsen, im Raum angeben. Der zeitliche Verlauf der Winkel bestimmt dann die Bewegungsfunktion des Kreisels. In diesem System können die Massenträgheitsmomente um nicht festgehaltene Achsen zeitlich variabel sein.

Im mitrotierenden körperfesten Bezugssystem sind die Bewegungsgleichungen besonders leicht zu formulieren, denn nur dort sind die Trägheitsmomente zeitlich konstant. Die Bewegung wird hier durch zusätzlich wirkende Trägheitskräfte beeinflusst. Diese sind die Euler-Kraft und die Fliehkraft. Corioliskräfte können nicht auftreten, weil beim Starrkörper eine Bewegung seiner Massenpunkte relativ zum Körper ausgeschlossen ist.

Gelegentlich wird bei symmetrischen Kreiseln noch ein anschauliches System verwendet, bei dem eine Achse mit der Figurenachse übereinstimmt, die anderen Achsen aber an der Rotation nicht teilnehmen. Hier wirken dann alle drei Formen der Trägheitskräfte: Euler-, Flieh- und Corioliskraft.

Die Bezugssysteme stellen sich mathematisch als Basisvektoren ${\hat {g}}_{1,2,3}$ dar, mit denen vektorielle Größen ausgedrückt werden. Die Zeitableitung solcher vektorieller Größen, beispielsweise des Wegs ${\vec {r}}$ , teilt sich im rotierenden Bezugssystem auf in einen Anteil, der auf die Relativbewegung im Bezugssystem zurückgeht, und einen zusätzlichen, der durch die Rotation des Bezugssystems beigetragen wird:

${\begin{aligned}{\dot {\vec {r}}}=&{\frac {\mathrm {d} }{\mathrm {d} t}}\sum _{i=1}^{3}r_{i}{\hat {g}}_{i}=\sum _{i=1}^{3}{\dot {r}}_{i}{\hat {g}}_{i}+\sum _{i=1}^{3}r_{i}{\dot {\hat {g}}}_{i}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {r}}+{\vec {\omega }}\times {\vec {r}}\end{aligned}}$

Darin ist ${\tfrac {\mathrm {d} '}{\mathrm {d} t}}$ die „relative Zeitableitung“, die auch als ${\tfrac {\mathrm {d} _{r}}{\mathrm {d} t}}$ notiert wird und bei der die Basisvektoren des Bezugssystems als konstant angenommen werden. Bei der Winkelgeschwindigkeit stimmen die Zeitableitung und die relative Zeitableitung im Hauptachsensystem überein:

${\dot {\vec {\omega }}}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {\omega }}+{\vec {\omega }}\times {\vec {\omega }}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {\omega }}=\sum _{i=1}^{3}{\dot {\omega }}_{i}{\hat {e}}_{i}$

Darin stehen ${\hat {e}}_{1,2,3}$ für das körperfeste, mitrotierende Hauptachsensystem.

Freiheitsgrade des Kreisels

Der rotierende Kreisel besitzt fünf Freiheitsgrade: drei Winkel und die Position des Schwerpunkts relativ zum Stützpunkt, wobei der Abstand zwischen Schwer- und Stützpunkt konstant ist. Sind also fünf unabhängige Erhaltungsgrößen der Kreiselbewegung gefunden, dann ist die Bewegungsgleichung gelöst. Es genügen sogar nur vier, denn mit der Jacobi'schen Multiplikatoren Methode kann aus vier unabhängigen Integralen ein fünftes konstruiert werden.

Kinetik von Kreiseln

Die Kinetik der Kreisel beschreibt die Eigenschaften ihrer Bewegung, die von der Masse abhängen.

Trägheitstensor, Hauptträgheitsmomente und Hauptachsen

→ Hauptartikel: Trägheitstensor

Der Trägheitstensor hat bei Drehbewegungen eine vergleichbare Rolle wie die Masse bei geradlinigen Bewegungen und ist deshalb eine zentrale Größe in der Kreiseltheorie. Bei einem aus einzelnen Massenpunkten aufgebauten starren Körper berechnet sich der Trägheitstensor aus der Summe

$\mathbf {\Theta } :=\sum _{i}m_{i}[({\vec {r}}_{i}\cdot {\vec {r}}_{i})\mathbf {1} -{\vec {r}}_{i}\otimes {\vec {r}}_{i}]=\sum _{i,j=1}^{3}\Theta _{ij}{\hat {g}}_{i}\otimes {\hat {g}}_{j}=\sum _{i=1}^{3}\Theta _{i}{\hat {e}}_{i}\otimes {\hat {e}}_{i}$

Die Summe ist über alle Massenpunkte zu erstrecken, deren Position relativ zum Stützpunkt darin mit ${\vec {r}}_{i}$ bezeichnet wird und m_i ist deren Masse. Diese Darstellung des Kreisels mittels ihn aufbauender Massenpunkte wird auch im Folgenden noch benutzt.

Die Vektoren ${\hat {g}}_{1,2,3}$ sind eine beliebige Basis, das Rechenzeichen „·“ bildet das Skalarprodukt, ⊗ das dyadischen Produkt von Vektoren und 1 ist der Einheitstensor. Die Komponenten Θ_ij des Trägheitstensors sind in einem körperfesten System konstant, im Inertialsystem, in dem sich der Kreisel dreht, jedoch möglicher Weise zeitabhängig. Die letzte Darstellung zeigt den Trägheitstensor in seiner Hauptachsendarstellung mit Hauptträgheitmomenten Θ_1,2,3 und Hauptträgheitsachsen oder kurz Hauptachsen ${\hat {e}}_{1,2,3}$ . Die Hauptachsen sind körperfest und drehen mit dem Kreisel mit. Der Trägheitstensor ist symmetrisch und positiv definit.

Alle Massenträgheitsmomente, Drehimpulse und Drehmomente werden in der Kreiseltheorie immer bezüglich des Stützpunkts aufgestellt.

Drehimpuls von Kreiseln

Bei einem wie oben aus einzelnen Massenpunkten aufgebauten starren Körper kann mit obiger Geschwindigkeitsverteilung der Eigendrehimpuls relativ zum Stützpunkt als Summe berechnet werden:

${\vec {L}}:=\sum _{i}{\vec {r}}_{i}\times {\vec {p}}_{i}=\sum _{i}m_{i}{\vec {r}}_{i}\times ({\vec {\omega }}\times {\vec {r}}_{i})=\mathbf {\Theta } \cdot {\vec {\omega }}$

Darin bezeichnet ${\vec {p}}_{i}=m_{i}{\vec {v}}_{i}=m_{i}{\vec {\omega }}\times {\vec {r}}_{i}$ den aktuellen Impuls des i-ten Massenpunkts. Ein Vergleich von ${\vec {p}}=m{\vec {v}}$ mit ${\vec {L}}=\mathbf {\Theta } \cdot {\vec {\omega }}$ zeigt, dass der Trägheitstensor für Drehungen eine vergleichbare Rolle wie die Masse für Translationsbewegungen spielt.

Mechanische Energie von Kreiseln

Die Rotationsenergie eines starren Körpers, der sich wie voraus gehend aus einzelnen Massenpunkten zusammen setzt, ergibt sich mit obiger Geschwindigkeitsverteilung zu

${\begin{aligned}E_{\mathrm {rot} }:=&{\frac {1}{2}}\sum _{i}m_{i}{\vec {v}}({\vec {r}}_{i},t)^{2}={\frac {1}{2}}\sum _{i}m_{i}({\vec {\omega }}\times {\vec {r}}_{i})^{2}\\=&{\frac {1}{2}}{\vec {\omega }}\cdot \mathbf {\Theta } \cdot {\vec {\omega }}={\frac {1}{2}}{\vec {L}}\cdot \mathbf {\Theta } ^{-1}\cdot {\vec {L}}={\frac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}\end{aligned}}$

Weil also bei einer Drehung das Skalarprodukt von Winkelgeschwindigkeit und Drehimpuls immer positiv ist, schließen sie immer einen spitzen Winkel ein.

In einem Schwerefeld mit konstanter Schwerebeschleunigung ${\vec {g}}$ besitzt der Starrkörper die Lageenergie

$E_{\mathrm {pot} }=-\sum _{i}m_{i}({\vec {r}}_{i}\cdot {\vec {g}})=-{\vec {g}}\cdot \sum _{i}m_{i}{\vec {r}}_{i}=-m{\vec {g}}\cdot {\vec {s}}$

Darin ist $\textstyle m:=\sum _{i}m_{i}$ die Masse und $\textstyle {\vec {s}}:={\tfrac {1}{m}}\sum _{i}m_{i}{\vec {r}}_{i}$ der Massenmittelpunkt des Starrkörpers relativ zum Stützpunkt. Die Lageenergie nimmt also entgegen der Schwerebeschleunigung, im Schwerefeld der Erde also mit der Höhe, zu. Im körperfesten Hauptachsensystem haben die Schwerebeschleunigung und der Massenmittelpunkt die Koordinaten:

${\begin{aligned}{\vec {g}}=&g(n_{1}{\hat {e}}_{1}+n_{2}{\hat {e}}_{2}+n_{3}{\hat {e}}_{3}),\quad g=|{\vec {g}}|\\{\vec {s}}=&s_{1}{\hat {e}}_{1}+s_{2}{\hat {e}}_{2}+s_{3}{\hat {e}}_{3}\end{aligned}}$

mit Konstanten s_1,2,3 im Hauptachsensystem. Damit lautet die Lageenergie

$E_{\mathrm {pot} }=-m{\vec {g}}\cdot {\vec {s}}=-mg(s_{1}n_{1}+s_{2}n_{2}+s_{3}n_{3})$

In der Literatur werden die Komponenten n_1,2,3 der Schwerkraftrichtung auch mit γ, γ', γ'' bezeichnet.

Wenn der Schwerpunkt der Stützpunkt ist ( ${\vec {s}}={\vec {0}}$ ), dann hat die Schwerebeschleunigung keinen Einfluss auf die Bewegung des Kreisels, was beim eulerschen Kreisel der Fall ist. Im Gegensatz dazu liegt beim schweren Kreisel der Schwerpunkt nicht im Stützpunkt und das Schwerefeld beeinflusst die Kreiselbewegung durch ein Moment

${\vec {M}}={\vec {s}}\times m{\vec {g}}=mg{\begin{pmatrix}s_{2}n_{3}-s_{3}n_{2}\\s_{3}n_{1}-s_{1}n_{3}\\s_{1}n_{2}-s_{2}n_{1}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}$

Die letzte Darstellung als Spaltenvektor bezieht sich auf das Hauptachsensystem.

Schranken für Drehimpuls und Rotationsenergie

Der Drehbewegung eines Kreisels kann jederzeit zum einen ein Drehimpulsbetrag $L:=|{\vec {L}}|$ und zum anderen eine Rotationsenergie $E_\mathrm{rot}$ zugeordnet werden. Bei einem Kreisel liegen diese beiden Größen innerhalb der Schranken

$2\Theta _{1}E_{\mathrm {rot} }\leq L^{2}\leq 2\Theta _{3}E_{\mathrm {rot} }$ oder ${\frac {L^{2}}{2\Theta _{3}}}\leq E_{\mathrm {rot} }\leq {\frac {L^{2}}{2\Theta _{1}}}$

Darin wurde die übliche Anordnung Θ₁ < Θ₂ < Θ₃ der Hauptträgheitsmomente voraus gesetzt.

Denn im lokalen körperfesten Hauptachsensystem ausgedrückt gilt:

${\begin{aligned}L^{2}&=&(\mathbf {\Theta } \cdot {\vec {\omega }})\cdot (\mathbf {\Theta } \cdot {\vec {\omega }})&=&\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2}\\2E_{\mathrm {rot} }&=&{\vec {\omega }}\cdot \mathbf {\Theta } \cdot {\vec {\omega }}&=&\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2}\end{aligned}}$

Diese beiden Gleichungen stellen mathematisch Ellipsoide dar, die erste das Drallellipsoid, die zweite das Energieellipsoid, die im kräftefreien Fall – und nur dort – gleichbleibende Ausdehnung besitzen. Ein Punkt, der auf beiden Ellipsoiden liegt, muss die Bedingungen

${\begin{aligned}1=&{\frac {1}{L^{2}}}(\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2})={\frac {1}{2E_{\mathrm {rot} }}}(\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2})\\\rightarrow 0=&(2E_{\mathrm {rot} }\Theta _{1}-L^{2})\Theta _{1}\omega _{1}^{2}+(2E_{\mathrm {rot} }\Theta _{2}-L^{2})\Theta _{2}\omega _{2}^{2}+(2E_{\mathrm {rot} }\Theta _{3}-L^{2})\Theta _{3}\omega _{3}^{2}\\=&2\left(E_{\mathrm {rot} }-{\frac {L^{2}}{2\Theta _{1}}}\right)\Theta _{1}^{2}\omega _{1}^{2}+2\left(E_{\mathrm {rot} }-{\frac {L^{2}}{2\Theta _{2}}}\right)\Theta _{2}^{2}\omega _{2}^{2}+2\left(E_{\mathrm {rot} }-{\frac {L^{2}}{2\Theta _{3}}}\right)\Theta _{3}^{2}\omega _{3}^{2}\end{aligned}}$

erfüllen. In den letzten beiden Gleichungen sind alle Faktoren bis auf die Klammerausdrücke null oder positiv. Eine nicht-triviale Lösung existiert, wenn in den Gleichungen der kleinste Klammerausdruck nicht positiv und der größte nicht negativ ist. Mit den angenommenen Größenverhältnissen der Hauptträgheitsmomente stellen dies die obigen Schranken für das Drehimpulsbetragsquadrat und die Rotationsenergie sicher. Dann sind die Rotationsenergie und der Drehimpulsbetrag mit einer Drehbewegung des betrachteten Körpers verträglich.

Eulersche Kreiselgleichungen

→ Hauptartikel: Eulersche Gleichungen (Kreiseltheorie)

Die Euler’schen Kreiselgleichungen ergeben sich aus dem Drallsatz ${\vec {M}}={\dot {\vec {L}}}=-{\vec {K}}$ . Die Kreiselwirkung auf der rechten Seite steht für Trägheitseffekte im beschleunigten Bezugssystem:

${\begin{aligned}{\vec {K}}=&{\vec {K}}_{\text{Euler}}+{\vec {K}}_{\text{Zentrifugal}}\\{\vec {K}}_{\text{Euler}}=&\sum _{i}{\vec {r}}_{i}\times [-m_{i}{\dot {\vec {\omega }}}\times {\vec {r}}_{i}]=-\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}=-{\begin{pmatrix}\Theta _{1}{\dot {\omega }}_{1}\\\Theta _{2}{\dot {\omega }}_{2}\\\Theta _{3}{\dot {\omega }}_{3}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\\{\vec {K}}_{\text{Zentrifugal}}=&\sum _{i}{\vec {r}}_{i}\times [-m_{i}{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}}_{i})]=-{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}=-{\begin{pmatrix}(\Theta _{3}-\Theta _{2})\omega _{2}\omega _{3}\\(\Theta _{1}-\Theta _{3})\omega _{3}\omega _{1}\\(\Theta _{2}-\Theta _{1})\omega _{1}\omega _{2}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\end{aligned}}$

Die Vektoren in den eckigen Klammern stellen in der mittleren Gleichung die Euler-Kraft und unten die Zentrifugalkraft am Massenpunkt mit Masse m_i am Ort ${\vec {r}}_{i}$ im rotierenden Bezugssystem dar. Würde der Kreisel mit konstant gehaltener Winkelgeschwindigkeit ${\vec {\omega }}$ um die instantane Drehachse kreisen, dann würden die Zentrifugalkräfte ein resultierendes Moment haben, das gerade der obigen Summe entspricht. Da bei der wirklichen Bewegung die Drehachse jedoch ihre Lage beständig ändert, hat Louis Poinsot für diese Zentrifugalkräfte den Namen fiktive Zentrifugalkräfte vorgeschlagen.

In den Drallsatz eingesetzt ergibt sich mit den Kreiselwirkungen:

${\vec {M}}={\dot {\vec {L}}}=\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}+{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}={\frac {\mathrm {d} '}{\mathrm {d} t}}{\vec {L}}+{\vec {L}}\cdot \mathbf {\Theta } ^{-1}\times {\vec {L}}$

oder im körperfesten Hauptachsensystem ausgeschrieben:

${\begin{aligned}M_{1}=&\Theta _{1}{\dot {\omega }}_{1}+(\Theta _{3}-\Theta _{2})\omega _{2}\omega _{3}={\dot {L}}_{1}+\left({\frac {1}{\Theta _{2}}}-{\frac {1}{\Theta _{3}}}\right)L_{2}L_{3}\\M_{2}=&\Theta _{2}{\dot {\omega }}_{2}+(\Theta _{1}-\Theta _{3})\omega _{3}\omega _{1}={\dot {L}}_{2}+\left({\frac {1}{\Theta _{3}}}-{\frac {1}{\Theta _{1}}}\right)L_{3}L_{1}\\M_{3}=&\Theta _{3}{\dot {\omega }}_{3}+(\Theta _{2}-\Theta _{1})\omega _{1}\omega _{2}={\dot {L}}_{3}+\left({\frac {1}{\Theta _{1}}}-{\frac {1}{\Theta _{2}}}\right)L_{1}L_{2}\end{aligned}}$

Darin sind jeweils für k=1,2,3

M_k die von außen angreifenden Drehmomente,

Θ_k die Hauptträgheitsmomente,

L_k := Θ_kω_k die Drehimpulse,

ω_k die Winkelgeschwindigkeiten und

${\dot {\omega }}_{k}$ die Winkelbeschleunigungen

im Hauptachsensystem.

Lagrange- und Hamiltonfunktion des Kreisels

Die Lagrangefunktion des Kreisels ist die Differenz der Rotationsenergie und der potentiellen Energie

${\mathcal {L}}=E_{\mathrm {rot} }-E_{\mathrm {pot} }={\frac {L_{1}^{2}}{2\Theta _{1}}}+{\frac {L_{2}^{2}}{2\Theta _{2}}}+{\frac {L_{3}^{2}}{2\Theta _{3}}}+mg(s_{1}n_{1}+s_{2}n_{2}+s_{3}n_{3})$

Die Lagrange-Funktion kann mit den Euler-Winkeln ausgedrückt werden, deren zeitlicher Verlauf dann aus den Lagrangegleichungen resultieren.

Die Hamiltonfunktion H des Kreisels ist die Summe aus Rotationsenergie und der potentiellen Energie:

$H=E_{\mathrm {rot} }+E_{\mathrm {pot} }={\frac {L_{1}^{2}}{2\Theta _{1}}}+{\frac {L_{2}^{2}}{2\Theta _{2}}}+{\frac {L_{3}^{2}}{2\Theta _{3}}}-mg(s_{1}n_{1}+s_{2}n_{2}+s_{3}n_{3})$

Die Euler-Poisson Gleichungen können mit ihr und der Poisson-Klammer {} ausgedrückt werden:

${\dot {L}}_{i}=\{L_{i},H\},\quad {\dot {n}}_{i}=\{n_{i},H\}\quad {\text{für}}\;i=1,2,3$

Diese Bewegungsgleichungen lassen sich auch in der Vektorform^[1]

${\begin{aligned}{\dot {M}}=&M\times {\frac {\partial H}{\partial M}}+\gamma \times {\frac {\partial H}{\partial \gamma }}\\{\dot {\gamma }}=&\gamma \times {\frac {\partial H}{\partial M}}\end{aligned}}$

schreiben. Darin ist M der Koordinatenvektor des Drehimpulses und γ der Koordinatenvektor des Einheitsvektors in Richtung der Schwerebeschleunigung jeweils bezüglich des Hauptachsensystems.

Die Poisson Algebra e(3) dieser Variablen ist gegeben durch

$\{L_{i},L_{j}\}=-\varepsilon _{ijk}L_{k},\quad \{L_{i},n_{j}\}=-\varepsilon _{ijk}n_{k},\quad \{n_{i},n_{j}\}=0$

Darin ist ε_ijk das Levi-Civita-Symbol. Es gibt zwei Casimir Funktionen F₁ = M · γ und F₂ = γ², die bezüglich der Poisson-Klammer mit jeder Funktion von M und γ kommunizieren und die auch gleichzeitig Integrale der Hamiltonfunktion sind.

Lösungen der Kreiselgleichungen

Für die technische Anwendung gibt es bedeutsame Spezialfälle, bei denen sich die Kreiselgleichungen soweit vereinfachen, dass sie integrabel sind. In diesen Fällen weisen die Trajektorien des Kreisels einen periodischen Verlauf auf, können die verschiedenen Bewegungsmodi klassifiziert und die Zeitfunktionen der Variablen sowie ihre geometrische Bedeutung angegeben werden. Insbesondere beim Kowalewskaja-Kreisel und im Goryachew-Chaplygin Fall sind die analytischen Lösungen so kompliziert, dass die Herausarbeitung der vorgenannten typischen Eigenschaften der Bewegung äußerst aufwändig ist. Hier helfen topologische Analyse (Bifurkationsdiagramm), Stabilitätsanalyse, Phasenraum-Diagramme und Computeranimationen dabei, Einblicke in die Vorgänge im Kreisel zu erhalten und deren typischen Eigenschaften heraus zu arbeiten. Die so erzielten Ergebnisse können praktische Anwendungen motivieren.

Die folgende Tabelle gibt eine Übersicht über die Fälle, in denen bisher exakte Lösungen der Bewegungsgleichungen gelungen sind.

Entdecker	Hauptträgheits- momente	Lage des Schwerpunkts	Anfangsbedingungen (t = 0)
Euler Euler-Kreisel	beliebig	s₁=s₂=s₃=0	beliebig
Lagrange siehe Lagrange-Kreisel	A=B	s₁=s₂=0, s₃≠0	beliebig
Sofia Kowalewskaja siehe Kowalewskaja-Kreisel	A=B=2C	$s_{1}^{2}+s_{2}^{2}\neq 0,\,s_{3}=0$	beliebig
Wilhelm Hess Hesssches Pendel	beliebig	${\frac {s_{1}}{s_{3}}}={\sqrt {\frac {C(A-B)}{A(B-C)}}}$ s₂=0	${\vec {L}}\cdot {\vec {s}}=0$
Gorjatschew und Chaplygin siehe Goryachew-Chaplygin-Kreisel	A=B=4C	$s_{1}^{2}+s_{2}^{2}\neq 0,\,s_{3}=0$	L_z=0
Merzalow	A=B=4C	$s_{1}^{2}+s_{2}^{2}\neq 0,\,s_{3}=0$	ω₃ = 0
Bobylev und Steklow siehe Bobylew-Steklow-Lösung	2A=C	s₁=s₂=0, s₃≠0	${\dot {\omega }}_{2}=\omega _{2}=0$
Staude Staude-Drehung	beliebig	beliebig	${\vec {\omega }}\times {\hat {e}}_{z}=0$ $({\vec {\omega }}\times {\vec {L}})\cdot {\vec {s}}=0$
Grioli Griolische Präzession	beliebig	${\frac {s_{1}}{s_{3}}}={\sqrt {\frac {A-B}{B-C}}}$ s₂=0	Bis auf einen Freiheitsgrad eindeutig festgelegt

Anmerkungen

↑ Die Fréchet-Ableitung einer skalaren Funktion $f({\vec {v}})$ nach einem Vektor ${\vec {v}}$ ist der Vektor ${\vec {A}}$ für den - sofern er existiert - gilt:

${\vec {A}}\cdot {\vec {h}}=\left.{\frac {\mathrm {d} }{\mathrm {d} s}}f({\vec {v}}+s{\vec {h}})\right|_{s=0}=\lim _{s\rightarrow 0}{\frac {f({\vec {v}}+s{\vec {h}})-f({\vec {v}})}{s}}\quad \forall \;{\vec {h}}$
Darin ist $s\in \mathbb {R}$ und „·“ das Frobenius-Skalarprodukt. Dann wird auch

${\frac {\partial f}{\partial {\vec {v}}}}={\vec {A}}$
geschrieben.

Basierend auf einem Artikel in:

Wikipedia.de