Dodekaeder
| Regelmäßiges Pentagondodekaeder | |
|---|---|
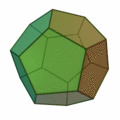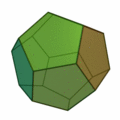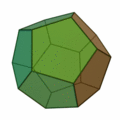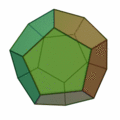 | |
| Art der Seitenflächen | regelmäßige Fünfecke |
| Anzahl der Flächen | 12 |
| Anzahl der Ecken | 20 |
| Anzahl der Kanten | 30 |
| Schläfli-Symbol | {5,3} |
| dual zu | Ikosaeder |
| Körpernetz | |
| Anzahl verschiedener Netze | 43380 |
| Anzahl Kanten in einer Ecke | 3 |
| Anzahl Ecken einer Fläche | 5 |
Das Dodekaeder [ˌdodekaˈʔeːdər] (von griech. Zwölfflächner; dt. auch (das) Zwölfflach) ist ein Körper mit zwölf Flächen. In der Regel ist damit ein platonischer Körper gemeint, nämlich das (regelmäßige) Pentagondodekaeder, ein Körper mit
- 12 (kongruenten) regelmäßigen Fünfecken als Flächen
- 20 Ecken, in denen jeweils drei dieser Fünfecke zusammentreffen
- 30 (gleich langen) Kanten, von denen jede die Seite von zwei Fünfecken ist.
Es gibt aber auch andere Dodekaeder von hoher Symmetrie.
Das regelmäßige Pentagondodekaeder
Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Dodekaeder ein reguläres Polyeder. Es hat:
- sechs fünfzählige Drehachsen (durch gegenüberliegende Flächenmittelpunkte)
- zehn dreizählige Drehachsen (durch gegenüberliegende Ecken)
- fünfzehn zweizählige Drehachsen (durch die Mittelpunkte gegenüberliegender Kanten)
- fünfzehn Symmetrieebenen (durch einander gegenüberliegende – und parallele – Kanten)
und ist
- inversionssymmetrisch (Punktspiegelung bezüglich des Dodekaedermittelpunkts)
Insgesamt hat die Symmetriegruppe des Dodekaeders – die
Dodekaeder- oder Ikosaedergruppe –
120 Elemente. Die 60 orientierungserhaltenden
Symmetrien entsprechen der alternierenden
Gruppe .
Manchmal wird auch diese Untergruppe „Ikosaedergruppe“ genannt. Die volle
Symmetriegruppe ist isomorph zu dem direkten Produkt
.
Dass das Produkt direkt ist, sieht man daran, dass die Punktspiegelung am
Mittelpunkt mit den Drehungen kommutiert.
Die Symmetrie des Dodekaeders ist durch die hier auftretenden fünfzähligen Symmetrieachsen mit einer periodischen Raumstruktur nicht verträglich (siehe Parkettierung). Es kann daher kein Kristallgitter mit Ikosaedersymmetrie geben (vgl. jedoch Quasikristalle).
Zur Struktur
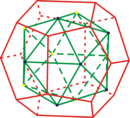
Das Ikosaeder ist das zum Dodekaeder duale Polyeder (und umgekehrt).
Mit Hilfe von Dodekaeder und Ikosaeder können zahlreiche Körper konstruiert werden, die ebenfalls die Dodekaedergruppe als Symmetriegruppe haben. So erhält man zum Beispiel
- das abgestumpfte Dodekaeder mit 12 Zehnecken und 20 Dreiecken (durch Abstumpfung der Ecken eines Dodekaeders)
- das Ikosidodekaeder mit 12 Fünfecken und 20 Dreiecken
- das abgestumpfte Ikosaeder mit 12 Fünfecken und 20 Sechsecken als Durchschnitt eines Dodekaeders mit einem Ikosaeder (ähnlich einem Fußball; siehe auch archimedische Körper, Fullerene)
- und das Rhombentriakontaeder mit 12 + 20 = 32 Ecken und 30 Rhomben als Flächen (Es entsteht durch das Aufsetzen gerader Pyramiden auf das Dodekaeder, von denen je zwei Seitenflächen einander ergänzen, d.h. in einer Ebene liegen und eine Kante gemein haben.)
Aus den Kanten des Dodekaeders kann man drei Paare gegenüber liegender (also insgesamt sechs) Kanten so auswählen, dass diese Paare drei kongruente, zueinander paarweise orthogonale Rechtecke aufspannen. Die restlichen acht Ecken bilden dann die Ecken eines (dem Dodekaeder eingeschriebenen) Würfels. Insgesamt gibt es fünf derartige Positionen, wobei jede Kante des Dodekaeders zu genau einer solchen Position gehört, und jede Ecke Eckpunkt von zwei einbeschriebenen Würfeln ist. Die Symmetriegruppe des Dodekaeders bewirkt alle 5!=120 Permutationen dieser fünf Positionen bzw. Würfel.
Da die Kanten des einbeschriebenen Würfels Diagonalen der Fünfecke sind, entspricht das Verhältnis der Längen der Kanten des Dodekaeders und jener eines eingeschriebenen Würfels dem Goldenen Schnitt.
Formeln
| Größen eines Dodekaeders mit Kantenlänge a | |
|---|---|
| Volumen | |
| Oberflächeninhalt | |
| Umkugelradius | |
| Kantenkugelradius | |
| Inkugelradius | |
| Verhältnis von Volumen zu Umkugelvolumen |
|
| Flächenwinkel ≈ 116° 33′ 54″ |
|
| Flächen-Kanten-Winkel ≈ 121° 43′ 3″ |
|
| Eckenraumwinkel ≈ 0,9428 π |
|
Anwendungen


(eine Zauberwürfel-Variante)
- Einige geodätische Kuppeln sind Polyeder, die vom Dodekaeder abgeleitet sind, indem die Fünfecke weiter in (gleichschenkelige) Dreiecke unterteilt werden.
- Es gibt dodekaederförmige Spielwürfel.
- Dodekaeder werden auch als originelle Wertstoff-Sammelbehälter (zum Beispiel in Paris) eingesetzt.
- In der Bauakustik werden dodekaederförmige Lautsprecher verwendet, um eine möglichst gute Kugelcharakteristik zu erhalten.
- Statt einer Glaskugel werden kristallene Zwölfflächner zur Raumausleuchtung verwendet.
- Der Verwendungszweck des römischen Pentagondodekaeders ist bis heute unklar.
- Ein Dodekaeder kann auch als Jahres-Kalender verwendet werden: jeder Monat erhält ein eigenes Fünfeck.
- Sowohl Megaminx als auch Alexander’s Star sind Varianten des Zauberwürfels in Form eines Dodekaeders als dreidimensionales Puzzle.
- In Waldorfschulen ist der Grundstein, der traditionell am Eingangsportal einer jeden Schule platziert wird, ein kupfernes Pentagondodekaeder.
Sonstiges
- Im Science-Fiction-Film Contact (1997) ist die Transportkugel in ein Gitter eingebettet, das die Form eines Dodekaeders hat.
Das kubische Pentagondodekaeder
Das kubische Pentagondodekaeder kann äußerlich leicht mit dem regelmäßigen Pentagondodekaeder verwechselt werden. Es hat ebenfalls 12 Flächen, 20 Ecken und 30 Kanten. Die Flächen (Fünfecke) sind aber nicht gleichseitig. Jede der 12 Flächen hat vier kürzere und eine längere Kante. Insgesamt besitzt das Polyeder 24 kürzere und 6 längere Kanten. Es besitzt dabei kubische Symmetrie. In der Natur kommt Pyrit (FeS2) manchmal in der Gestalt von kubischen Pentagondodekaedern vor. Deshalb wird das kubische Pentagondodekaeder auch Pyrit-Dodekaeder oder Pyritoeder genannt. Bei Kristallen sind fünfzählige Achsen unmöglich, wie das reguläre Pentagondodekaeder sie besitzt, weil es keine lückenlose periodische Flächenfüllung mit fünfzähliger Symmetrie gibt. Nur bei nicht streng periodischen „Kristallen“, also Quasikristallen, ist ein reguläres Pentagondodekaeder denkbar.
Andere Dodekaeder
Andere regelmäßige Dodekaeder sind z.B.:
- Das Rhombendodekaeder besitzt 12 kongruente Rhomben als Flächen, 14 Ecken und 24 Kanten. Es bildet die typische Kristallform der Granate.
- Das Trigondodekaeder besitzt 12 kongruente gleichseitige Dreiecke als Flächen, 8 Ecken und 18 Kanten.
- Ausgehöhltes Dodekaeder
- Großes Dodekaeder
- Rhombenikosidodekaeder
- Verlängertes Rhombendodekaeder


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.06. 2022