Ikosaederstumpf
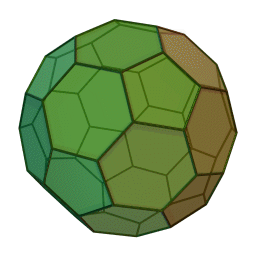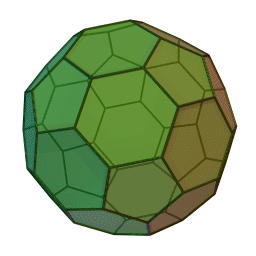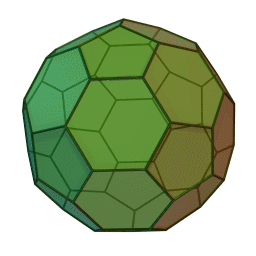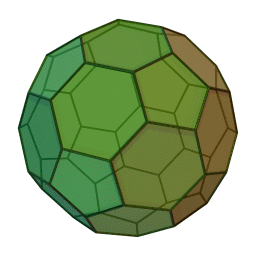
3D-Ansicht
eines abgestumpften Ikosaeders

Fußball:
Projektion der Flächen eines Ikosaederstumpfes auf die Kugeloberfläche
Der Ikosaederstumpf (auch Fußballkörper genannt) ist ein Polyeder (Vielflächner), das durch Abstumpfung der Ecken eines Ikosaeders entsteht und zu den archimedischen Körpern zählt. Anstatt der zwölf Ecken des Ikosaeders befinden sich nun dort zwölf regelmäßige Fünfecke; die 20 Dreiecke des Ikosaeders werden zu regelmäßigen Sechsecken. Das Polyeder setzt sich somit aus insgesamt 32 Flächen zusammen und hat 60 Ecken sowie 90 Kanten.
Beim regelmäßigen Ikosaederstumpf, also dem Fußballkörper, sind alle 90 Kanten gleich lang.
Der zum Ikosaederstumpf duale Körper ist das Pentakisdodekaeder.
Das mit Abstand am besten untersuchte Fullerenmolekül C60 besitzt die Struktur eines Ikosaederstumpfes.
Formeln
| Größen eines regelmäßigen Ikosaederstumpfs mit Kantenlänge a | |
|---|---|
| Volumen | |
| Oberflächeninhalt | |
| Umkugelradius | |
| 1. Inkugelradius (Pentagon) |
|
| 2. Inkugelradius (Hexagon) |
|
| Kantenkugelradius | |
| 1. Flächenwinkel (Hexagon–Hexagon) ≈ 138° 11′ 23″ |
|
| 2.
Flächenwinkel (Hexagon–Pentagon) ≈ 142° 37′ 21″ |
|
| Eckenraumwinkel ≈ 1,3524 π |
|


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.06. 2021