Halbwertsschicht

Als Halbwertsschicht oder Halbwertsdicke bezeichnet man diejenige Dicke eines durchstrahlten Materials, die bei elektromagnetischer Strahlung wie etwa Gamma- oder Röntgenstrahlung die Strahlungsintensität – und damit insbesondere die Dosisleistung – um die Hälfte reduziert. Die Halbwertsdicke hängt wie der Absorptionskoeffizient von den spezifischen Eigenschaften des Materials und der Photonenenergie der auftreffenden Strahlung ab.

Die Halbwertsdicke kann nur zur überschlägigen Dimensionierung einfacher Abschirmungen dienen, da vielfältige physikalische Effekte (zum Beispiel Dosisaufbau, Streuung, Skyshine-Effekte) unberücksichtigt bleiben. Genaue Ergebnisse erfordern zum Beispiel Monte-Carlo-Simulationen oder Transportrechnungen (numerische Berechnungen auf der Grundlage der Boltzmannschen Transportgleichung).

Der Begriff Zehntelwertsdicke ist analog zu betrachten: das Durchlaufen dieser Dicke senkt die Intensität auf ein Zehntel des ursprünglichen Werts.

Exponentielle Abnahme mit der Eindringtiefe

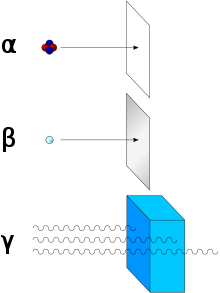
Alphastrahlung (α) wird durch ein Blatt Papier, Betastrahlung (β) durch ein Metallblech von einigen Millimeter Dicke vollständig absorbiert; zur hinreichenden Schwächung von Gammastrahlung (γ) braucht man – je nach Energie dieser Strahlung – mehrere Zentimeter bis Dezimeter eines Materials möglichst hoher Dichte (siehe Abschirmung (Strahlung)).

Im Gegensatz zu Alpha- und Betastrahlung besitzt Gammastrahlung keine maximale Reichweite. Die Intensität der Gammastrahlung wird beim Durchgang durch Materie kontinuierlich geschwächt.

Das Verhältnis aus der Dosisleistung ${\dot H}_{0}$ , die ohne Abschirmung im Strahlengang ermittelt wird, und der Dosisleistung ${\dot H}_{{\mathrm {u}}}$ der ungestreuten Strahlung am gleichen Ort mit Abschirmmaterial der Dicke wird als (materieller) Schwächungsfaktor $S_{{\mathrm {u}}}$ der ungestreuten Strahlung bezeichnet:

$S_{{\mathrm {u}}}={\frac {{\dot H}_{0}}{{\dot H}_{{\mathrm {u}}}}}$

Für den reziproken Schwächungsfaktor gilt die Formel

${\frac {1}{S_{{\mathrm {u}}}}}={\frac {{\dot H}_{{\mathrm {u}}}}{{\dot H}_{0}}}={{\mathrm {e}}^{{-\mu \cdot d}}}$ .

Hierbei bezeichnet $\mu$ den Schwächungskoeffizienten. Für die Halbwertsschichtdicke $d_{{\text{1/2}}}$ gilt definitionsgemäß

${\frac {1}{S_{{\mathrm {u}}}}}={\frac {{\dot H}_{{\mathrm {u}}}}{{\dot H}_{0}}}={{\mathrm {e}}^{{-\mu \cdot d_{{\text{1/2}}}}}}={\frac {1}{2}}$ .

Somit ergibt sich die Halbwertsschichtdicke $d_{{\text{1/2}}}$ aus dem Schwächungskoeffizienten $\mu$ nach

$d_{{\text{1/2}}}={\frac {\ln 2}{\mu }}\approx {\frac {0{,}6931}{\mu }}$

oder umgekehrt

$\mu ={\frac {\ln 2}{d_{{\text{1/2}}}}}\approx {\frac {0{,}6931}{d_{{\text{1/2}}}}}$ .

Für die Dosisleistung ${\dot H}_{{\mathrm {u}}}$ hinter einer Abschirmung mit einer beliebigen Dicke erhält man damit

${\dot {H}}_{\mathrm {u} }={\dot {H}}_{0}\cdot {\frac {1}{S_{\mathrm {u} }}}={\dot {H}}_{0}\cdot {\mathrm {e} ^{-\mu \cdot d}}={\dot {H}}_{0}\cdot {\mathrm {e} ^{-\ln(2)\cdot {\frac {d}{d_{\text{1/2}}}}}}={\frac {{\dot {H}}_{0}}{2^{\frac {d}{d_{\text{1/2}}}}}}$ .

Halbwertsschichtdicke für Gammastrahlun

Halbwertsschichtdicke d_1/2 für Gammastrahlung
	Luft	Blei	Wasser	Alu	Eisen	Graphit	Beton	Bleiglas	A title="Acryl" href="https://de.wikipedia.org/wiki/Acryl">-->Acryl
E_γ in MeV	in Meter	in Millimeter
0,1	35	0,107	41	15,2	2,4	20,3
0,2	44	0,62	51	21,1	6	25
0,3	50	1,56	58	24,8	8	28,8
0,4	56	2,65	65	27,8	9,4	32,4
0,5	62	3,85	72	30,5	10,5	35,4	33	13	70
0,6	67	4,92	77	33	11,5	38,3
0,8	76	6,9	88	37,7	13,2	44
1	84	8,7	108	42	14,7	48	50	24	90
1,5	101	11,7	121	51	18,1	59
2	121	13,4	141	60	20,8	69
3	145	14,6	175	73	24,4	87
4	174	14,7	204	83	26,7	101
5	196	14,4	230	91	28,1	115	100	45	200
6	213	14,1	251	97	28,9	125
8	242	13,4	286	106	29,7	144
10	265	12,6	315	112	29,7	158

Literatur

Hans-Gerrit Vogt, Heinrich Schultz: Grundzüge des praktischen Strahlenschutzes. 6. Auflage. Carl Hanser Verlag GmbH & Co. KG, München 2011, ISBN 978-3-446-42593-4.

Basierend auf einem Artikel in:

Wikipedia.de