
Kernmasse
Die Kernmasse
bezeichnet die Masse eines von allen Elektronen
der Hülle befreiten nackten
Atomkerns.
Sie unterscheidet sich von der Atommasse
um die Ruhemassen
der im Atom
gebundenen Elektronen und ihre Bindungsenergie
:
mit
Die Bindungsenergie
der Elektronenhülle kann experimentell nicht direkt bestimmt werden, stattdessen
ist man auf theoretische Abschätzungen
angewiesen. Die Berechnung nach dem Thomas-Fermi-Modell
liefert für ein Atom mit
Elektronen
den Näherungswert
(Formel 1).
Berechnete Bindungsenergien für alle Elektronen des Atoms können Tabellen von 1976 entnommen werden. Eine weitere Zahlenwertgleichung, die die Bindungsenergie aller Elektronen eines Atoms besser approximiert als die Formel 1 und die nach der Hartree-Fock-Slater-Methode abgeleitet wurde:
(Formel 2).
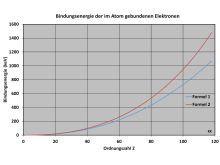
Die Abbildung zeigt die Kurvenverläufe für die Bindungsenergie der im Atom
gebundenen Elektronen in Abhängigkeit von der Ordnungszahl
für beide Formeln. Für Uran-Isotope 92U, also
,
ergibt sich eine totale elektronische Bindungsenergie nach Formel 1 von 600 keV
bzw. nach Formel 2 von 763 keV. Zum Vergleich sei daran erinnert, dass das
Energieäquivalent der Masse eines Elektron 511 keV beträgt.
Die Genauigkeit der berechneten Werte für die Größe
ist nicht bekannt. Vermutlich ist die Unsicherheit für Uran-Isotope in den
Tabellen von 1976
kleiner als 2 keV.
Bei praktischen Berechnungen (Kernmassen mit 6 bis 7 geltenden Ziffern)
fallen die Werte für
oft nicht ins Gewicht, dann gilt die Näherung:
Kernmassen können in Massenspektrometern sehr genau bestimmt werden, wenn das entsprechende Atom vollständig ionisiert ist. Dies ist jedoch nur bei niedrigen Ordnungszahlen mit vertretbarem Aufwand möglich. Heutzutage gibt es einige Messungen der Masse von vollständig (also nackten Atomkernen) oder nahezu vollständig ionisierten Atomen.
Atomkerne sind leichter als die Summe ihrer Bestandteile (Protonen- und Neutronenmassen):
mit
: Masse eines Protons
: Masse eines Neutrons
: Neutronenzahl.
Die fehlende Masse wird als Massendefekt
bezeichnet und entspricht genau der Bindungsenergie
des Atomkerns.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.09. 2023