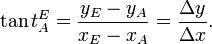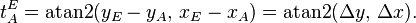Richtungswinkel
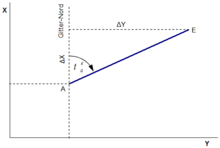
Richtungswinkel (üblicherweise mit 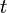 bezeichnet) ist eine in der Mathematik
und Geodäsie verwendete
Bezeichnung für den Winkel
zwischen der Nordrichtung (Gitternord)
und einer Geraden oder Strecke. Der
Richtungswinkel einer Strecke vom Punkt
bezeichnet) ist eine in der Mathematik
und Geodäsie verwendete
Bezeichnung für den Winkel
zwischen der Nordrichtung (Gitternord)
und einer Geraden oder Strecke. Der
Richtungswinkel einer Strecke vom Punkt 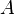 zum Punkt
zum Punkt 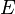 wird von der Parallelen
zur nach Norden ausgerichteten x-Achse
durch den Punkt
wird von der Parallelen
zur nach Norden ausgerichteten x-Achse
durch den Punkt 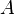 aus rechtsläufig, das heißt im Uhrzeigersinn, angegeben.
aus rechtsläufig, das heißt im Uhrzeigersinn, angegeben.
Gebräuchliche Schreibweisen für den Richtungswinkel sind 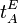 oder
oder 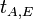 .
Dabei bezeichnet der Index
.
Dabei bezeichnet der Index 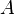 den Anfangs- oder Standpunkt und der zweite Index
den Anfangs- oder Standpunkt und der zweite Index 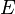 den End- oder Zielpunkt.
den End- oder Zielpunkt.
Für den Richtungswinkel in einem geodätischen Koordinatensystem, d.h. mit geodätisch positivem oder mathematisch negativem Drehsinn, gilt folgende Beziehung:
Bei der polaren
Koordinatenberechung aus kartesischen Koordinaten muss der
Quadrant berücksichtigt
werden, in dem der Richtungswinkel liegt. Dazu eignet sich die Funktion 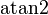 :
:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.02. 2021