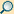Radarquerschnitt
Der Radarquerschnitt (englisch radar cross section, RCS, bei manchen Quellen auch als equivalent echoing area bezeichnet) gibt an, wie groß die Reflexion eines Gegenstandes zurück in Richtung der Quelle einer Funkwelle (Radar) ist. Er gibt die Größe einer isotrop reflektierenden Fläche an, die ein gleich hohes Radarecho wie der Gegenstand liefert.
Der Radarquerschnitt ist abhängig von der Form des Gegenstandes, der Materialbeschaffenheit sowie von Wellenlänge, Einfalls- und Ausfallswinkel der Strahlung.

Der Radarquerschnitt, in manchen Veröffentlichungen auch Rückstrahlfläche oder effektive Reflexionsfläche genannt, ist eine objektspezifische Größe, die auf die Entdeckungswahrscheinlichkeit eines Objektes durch ein Radargerät wesentlichen Einfluss hat. In mathematischen Formeln (zum Beispiel in der Radargleichung) wird die Rückstrahlfläche mit dem griechischen Buchstaben σ (Sigma) bezeichnet und hat die Maßeinheit Quadratmeter.
Ein hoher Radarquerschnitt ist z.B. für Schiffe, Bojen (Seezeichen), Brückendurchfahrten oder Wetterballons erwünscht, um sie besser orten zu können, und wird oft mit Radarreflektoren (Retroreflektoren für Mikrowellen) erreicht.
Ein geringer Radarquerschnitt ist heute eines der wesentlichen Qualitätsmerkmale eines militärischen Flugkörpers, da z.B. ein Flugzeug mit einem geringen Radarquerschnitt für gegnerische Radaranlagen schwer zu entdecken ist. Zur Verringerung des Radarquerschnitts wurden daher sogenannte Tarnkappentechniken entwickelt. Der Radarquerschnitt eines militärischen Flugkörpers gilt in der Regel als militärisches Geheimnis und wird nicht öffentlich bekanntgegeben.
Das nebenstehende Diagramm ist einer Veröffentlichung von M. I. Skolnik nachempfunden, die im Original ein Diagramm mit der experimentell ermittelten relativen Rückstrahlfläche σ/σ0 des B-26-Bombers „Invader“ bei einer Frequenz von 3 GHz zeigt.
Messung

Die Messung des Radarquerschnitts eines Objekts geschieht typischerweise mit Radargeräten. Sie kann im Freiland oder in einem Freifeldraum durchgeführt werden, der elektromagnetische Wellen der betreffenden Frequenz vollständig absorbiert.
Typische Werte für ein Zentimeterwellenradar sind:
- Insekt: 0,00001 m²
- Vogel: 0,01 m²
- Flugzeuge mit Tarnkappentechnik: < 0,1 m²
- Flugabwehrraketen: ≈ 0,1 m²
- Mensch: 1 m²
- kleines Kampfflugzeug: 2–3 m²
- großes Kampfflugzeug: 5–6 m²
- Transportflugzeug: bis zu 100 m²
- Winkelreflektor mit 1,5 m Kantenlänge: ≈ 20.000 m²
- Küstenmotorschiff (55 m Länge): 300–4000 m²
- Fregatte (103 m Länge): 5000–100.000 m²
- Containerschiff (212 m Länge): 10.000–80.000 m²
Berechnung
Die Rückstrahlfläche ist von vielen Faktoren abhängig. Eine analytische
Bestimmung der Rückstrahlfläche ist nur bei einfachen Körpern möglich. Sie ist
abhängig von der Körperform und der Wellenlänge, oder besser gesagt, vom
Verhältnis der Strukturabmessungen des Körpers zur Wellenlänge. Quantitativ gibt
der Radarquerschnitt eine effektive Fläche an, die die einlaufende Welle
einfängt und isotrop
in den Raum abstrahlt. Diese Formeln gelten nur für den optischen
(frequenzunabhängigen) Bereich, also für Objekte, deren Abmessungen mindestens
zehnmal größer als die Wellenlänge sind. Haben die Objekte annähernd die
Abmessung der Wellenlänge des anstrahlenden Radarstrahls, kommt es zu
Resonanzerscheinungen, die den Radarquerschnitt deutlich erhöhen. In drei
Dimensionen ist der Radarquerschnitt
definiert als:
Dabei ist
die Leistungsdichte auf dem Radarziel und
die gestreute Leistungsdichte in einem Abstand
vom Radarziel.
Alternativ lässt sich schreiben:
mit
– eingestrahlte Feldstärke
– gestreute Feldstärke
Einfache Formen haben, wenn sie groß gegenüber der Wellenlänge λ sind, folgende theoretische Radarquerschnitte σ:
Kugel mit dem Radius r:
Quer zur Strahlrichtung stehende Platte (ausgerichteter Planspiegel) mit der Fläche A:
Winkelreflektor (Retroreflektor) aus drei Quadratflächen mit den Seitenlängen a:
Anstelle von Messungen ist es heute üblich, den Radarquerschnitt durch Computersimulationen zu berechnen. So ist es bereits in der Entwurfsphase der Entwicklung von Militärflugzeugen oder anderen Radarzielen möglich, den Radarquerschnitt zu relativ geringen Kosten zu berechnen und entsprechend zu optimieren.
Verringerung des Radarquerschnitts

Passive Verfahren
Die Verringerung des Radarquerschnitts kann grundsätzlich durch
- die Formgebung
- die Verwendung absorbierenden Materials (in Harz gebundene Ferrit- oder Graphitpartikel)
- durchlässiges Material (Plastwerkstoffe)
erzielt werden.
Die (geringe) Reflexion an dielektrischen Stoffen kann analog zu optischen Verfahren durch geeignete Schichtdicken unterschiedlicher Materialarten weiter verringert werden, allerdings ist die Wirkung wellenlängenabhängig.
Ein Militärflugzeug wie etwa die Lockheed F-117 besitzt nicht nur eine Mikrowellen absorbierende Oberfläche, sondern auch eine Formgebung, die verhindert, dass Radarstrahlung zum Sender reflektiert wird: man verwendet gerade Flächen – die Wahrscheinlichkeit, dass sie senkrecht zur Quelle stehen, ist gering. Man vermeidet Innenkanten / Innenecken sowie jegliche Teile aus Metall an der Außenhaut. Besonders rechtwinkelige Innenecken aus Metall führen in einem weiten Bereich zu einer fast vollständigen Reflexion der eintreffenden Strahlung zum Sender.
Aktive Verfahren
Eine aktive Verringerung des Radarquerschnittes basiert auf destruktiver Interferenz. Das Radarsignal wird empfangen und mit fast gleicher Amplitude, aber um etwa 180° phasenversetzt wieder ausgesendet. Die Verstärker dazu arbeiten mit sehr geringer Verstärkung, um eine Selbsterregung zu vermeiden, sie gleichen also nur die Verluste der Antennen aus und drehen die Phase. Dieses Verfahren wird vor allem bei VHF- Radar angewendet.
Erhöhung des Radarquerschnittes

Passive Verfahren
U.a. in der zivilen Seefahrt, bei zivilen und militärischen Häfen und Flughäfen, an Seezeichen und Bojen, an Brückendurchfahrten und auch an Wetterballons werden Maßnahmen zur Erhöhung des Radarechos eingesetzt. Ziel ist es, sicher zu navigieren, zu orten und die Seewege zu koordinieren. Dazu werden Winkelreflektoren eingesetzt, die den Radarquerschnitt auf das Vieltausendfache ihrer geometrischen Fläche vergrößern.
Generell besitzen Gegenstände aus Metall ein höheres Radarecho als Nichtmetalle. Bereits relativ kleine Metallteile können daher eine Erhöhung des Radarquerschnittes bewirken, um z.B. ein Boot mit einem Kunststoffrumpf auf dem Radar sichtbar zu machen. Oft werden von solchen kleinen Booten kleine Radarziele mit Abmessungen im Zentimeterbereich mitgeführt, die im von Radaranlagen oft genutzten X-Band (ca. 6…12 GHz) bzw. im I-Band (Europa, 8…10 GHz) als resonanter Sekundärstrahler bereits ein erhöhtes Echo liefern und erst bei kürzeren Wellenlängen aufgrund ihrer Formgebung als Winkelreflektor wirken.
Aktive Verfahren
Es werden kommerzielle Radarreflektoren angeboten, die nach dem Transponderprinzip oder als Repeaterjammer arbeiten. Das Radarsignal wird empfangen und auf gleicher Frequenz verstärkt wieder ausgesendet. Diese Geräte haben den Vorteil, dass auch ein Warnton die Erfassung durch ein Radargerät signalisiert.
Die durch den Empfang und die Verarbeitung dem Radarecho auferlegte Zeitverzögerung darf nur einige Mikrosekunden betragen, um das Ziel auf dem Radarschirm nicht in allzu falscher Entfernung darzustellen. Moderne Geräte analysieren das Signal und senden die Antwort zeitsynchron eine Impulsfolgeperiode später wieder aus.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.06. 2021