Antiferromagnetismus
Der Antiferromagnetismus (griechisch αντί anti ‚gegen‘; lateinisch ferrum‚ Eisen‘; von griechisch μαγνῆτις magnetis (lithos) ‚Stein aus Magnesien‘) ist ein kooperatives, magnetisches Phänomen, welches u.a. von Louis Néel eingehend untersucht wurde.
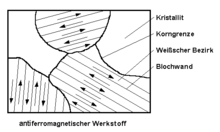
Überblick
Bei diesem Effekt sind die magnetischen Momente oder Spins der Atome mit einem konstanten, von Null verschiedenen Drehwinkel zueinander ausgerichtet und kompensieren sich exakt über den gesamten Kristall. Im einfachsten Fall ist dieser Drehwinkel 180°, so dass die Spins benachbarter Atome antiparallel zueinander stehen.
Beim bekannteren Ferromagnetismus sind die Spins dagegen parallel zueinander ausgerichtet, wodurch eine makroskopische Magnetisierung aufgebaut wird, während beim Antiferromagnetismus ohne ein angelegtes Magnetfeld die resultierende Magnetisierung Null ist. Beide Ordnungen sind nur bei hinreichend tiefen Temperaturen stabil. Beim Antiferromagnetismus zeigt die Permeabilität ein Maximum bei der Phasenübergangstemperatur, der Néel-Temperatur (benannt nach Louis Néel). Oberhalb der Néel-Temperatur, in der magnetisch ungeordneten Phase mit weitgehend beliebig orientierten Spins, ist das Verhalten des Materials paramagnetisch, und die Permeabilität nimmt mit steigender Temperatur ab.
Die antiferromagnetische Struktur lässt sich, genau wie andere magnetische Konfigurationen, insbesondere mit Hilfe einer Austauschwechselwirkung erklären. Abhängig von ihrem Vorzeichen kann man beispielsweise im Rahmen eines Ising-Modells mit Kopplungen, die sich auf Nachbarspins beschränken, leicht ferro- bzw. antiferromagnetische Anordnungen der magnetischen Momente beschreiben. Längerreichweitige oder konkurrierende Wechselwirkungen können zu komplizierteren magnetischen Strukturen führen (z.B. zu Spiralstrukturen).
Präzisierung
Der oben beschriebene Néel-Zustand (mit alternierenden Spinrichtungen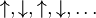 
)
ist genau genommen nicht der Grundzustand des Systems, sondern nur eine
quasi-klassische Näherung dafür, die sich besonders gut zur Beschreibung der
Anregungszustände, der sog. Spinwellen,
eignet, während der genaue quantenmechanische Grundzustand, außer in speziellen
Fällen, unbekannt ist, auf jeden Fall auch in den erwähnten Spezialfällen extrem
kompliziert (z.B. Bethe-Ansatz).
Dagegen ist im ferromagnetischen Fall der klassische Grundzustand (z.B.
alle Spins nach oben 
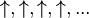) auch im quantenmechanisch Formalismus exakt, und die Beschreibung der
Anregungszustände (Spinwellen) entspricht im Falle des Ferromagnetismus fast
völlig dem klassischen Bild präzedierender Vektoren.
Siehe auch
Wikipedia.de
© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 30.05. 2019