Ränderung

Als Ränderung (engl.: Bordering Method) bezeichnet man ein Verfahren zur Verbesserung der Lösungseigenschaften linearer Gleichungssysteme. Das Verfahren kommt in der linearen Algebra und der Numerik zur Anwendung.

Einem linearen Gleichungssystem

mit singulärer oder schlecht konditionierter Systemmatrix $A\in {\mathbb {R}}^{{m\times n}}$ kann man durch Hinzufügen von Zeilen und Spalten zu und entsprechendes Vergrößern von und ein erweitertes lineares Gleichungssystem zuordnen, bei dem die Systemmatrix gut konditioniert (also auch regulär) ist. Die einfachen Beispiele in den nächsten zwei Abschnitten sollen das verdeutlichen. Die durch Zeilen und Spalten ergänzte Systemmatrix bezeichnet man auch als geränderte Matrix.

Beispiel (Regularisierung)

Gegeben sei das Gleichungssystem

$(0)(x_{1})=(1)$

mit der $1\times 1$ -Systemmatrix A=(0) , dem Einervektor $x=(x_{1})$ der Unbekannten und der rechten Seite b=(1) . Dieses kann durch Ränderung der Systemmatrix mit der Spalte $\left({\begin{matrix}1\\0\end{matrix}}\right)$ und der Zeile $\left({\begin{matrix}1&0\end{matrix}}\right)$ regularisiert werden:

$\left({\begin{matrix}0&\overline {1}\\\overline {1}&\overline {0}\end{matrix}}\right)\left({\begin{matrix}x_{1}\\\overline {x}_{2}\end{matrix}}\right)=\left({\begin{matrix}1\\\overline {0}\end{matrix}}\right).$

Die zu dem ursprünglichen System hinzugekommenen Einträge sind überstrichen. Das geränderte System hat die eindeutige Lösung $\overline x\in {\mathbb {R}}^{2}$ mit $x_{1}=0,\;\overline {x}_{2}=1$ . Davon ist die durch die Ränderung dem ursprünglichen Problem zugeordnete Lösung $x_{1}=0$ . Die Größe von $\overline {x}_{2}$ drückt aus, wie stark der regularisierende Einfluss der Ränderung ist.

Beispiel (Verbesserung der Kondition)

In diesem Beispiel sei $b\in {\mathbb {R}}^{2}$ ein bzgl. der euklidischen Norm mit 10 % Fehler behafteter Messwertvektor aus dem mit Hilfe der Gleichung

${\begin{matrix}\underbrace {{\begin{pmatrix}1&10\\0&1\end{pmatrix}}}&{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}&=&{\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}&\\A\end{matrix}}$

die Größen x_1,x_2 ermittelt werden sollen. Für $b={\begin{pmatrix}1\\0\end{pmatrix}}$ ergibt sich die Lösung $x={\begin{pmatrix}1\\0\end{pmatrix}}.$ Für die um ca 10 % abweichende (also innerhalb der Fehlertoleranz liegende) rechte Seite $b={\begin{pmatrix}1\\0.1\end{pmatrix}}$ ermittelt man die vollkommen andere Lösung $x={\begin{pmatrix}0\\0.1\end{pmatrix}}$ .

Ein Maß dafür, wie stark sich relative Fehler ${\frac {|\Delta b|}{|b|}}$ in der Messung auf den relativen Fehler ${\frac {|\Delta x|}{|x|}}$ des Rechenergebnisses auswirken, ist die Kondition der Systemmatrix

$\operatorname {cond}(A)=\max \left\{\left.{\frac {{\frac {|\Delta x|}{|x|}}}{{\frac {|\Delta b|}{|b|}}}}\;\right|\;b,\Delta b\in {\mathbb {R}}^{n}\setminus \{0\},\;Ax=b,\;A(x+\Delta x)=(b+\Delta b)\right\}.$

Für die spezielle Wahl von aus diesem Beispiel ergibt sich $\operatorname {cond}(A)\approx 102$ . Relative Fehler in den Messdaten können sich also durch die schlechte Kondition der Matrix ca. hundertfach im relativen Fehler der aus diesen Daten berechneten Größen niederschlagen.

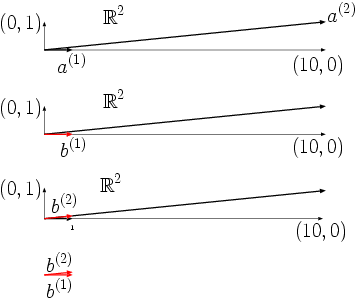
Dieser Effekt ist im folgenden Bild für die oben vorgegebenen rechten Seiten grafisch veranschaulicht. Aus dem oberen Teil des Bildes erkennt man, dass die zwei Spaltenvektoren $a^{{(1)}}:=\left({\begin{matrix}1\\0\end{matrix}}\right)$ und $a^{{(2)}}:={\begin{pmatrix}10\\1\end{pmatrix}}$ von beinahe linear abhängig voneinander sind.

Geometrische Interpretation der schlechten Kondition der Matrix

Dadurch fallen die im unteren Teil des Bildes rot dargestellten zwei rechten Seiten $b^{{(1)}}$ und $b^{{(2)}}$ , die sehr nahe beieinander liegen, in die Bildräume unterschiedlicher Spalten von und die Koeffizienten x_1,x_2 in

$a^{{(1)}}x_{1}+a^{{(2)}}x_{2}=Ax=b$

unterscheiden sich beim Wechsel von $b=b^{{(1)}}$ zu $b=b^{{(2)}}$ stark voneinander.

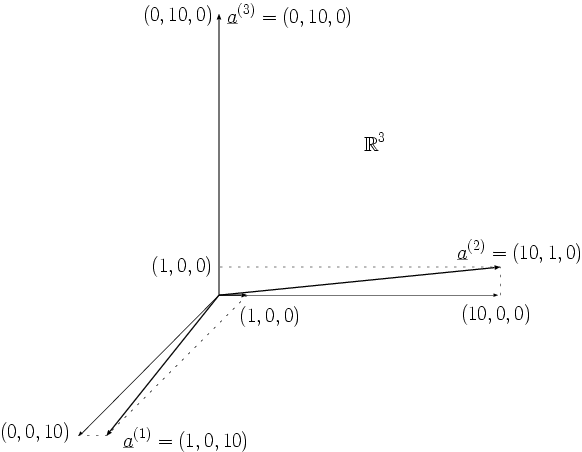
Effekt einer Ränderung: Das Hinzufügen einer zusätzlichen Zeile zu entspricht der Erweiterung des Wertebereiches von um eine Dimension vom $\mathbb {R} ^{2}$ zum $\mathbb {R} ^{3}$ und mit dem Ergänzen einer Spalte kommt ein neuer Spaltenvektor ${\overline {a}}^{(3)}$ hinzu. Durch geschickte Wahl der zusätzlichen Komponenten $\overline a_{3}^{{(1)}},\;\overline a_{3}^{{(2)}}$ und des zusätzlichen Spaltenvektors ${\overline {a}}^{(3)}$ erreicht man, dass die Spaltenvektoren der geränderten Matrix ${\overline {A}}:=\left({\overline {a}}^{(1)}\;{\overline {a}}^{(2)}\;{\overline {a}}^{(3)}\right)$ wesentlich besser voneinander separiert werden. Genauer wählt man die neuen Freiheitsgrade möglichst so, dass die Spalten ${\overline {a}}^{(1)},{\overline {a}}^{(2)},{\overline {a}}^{(3)}$ der geränderten Matrix ${\overline {A}}$ senkrecht aufeinander stehen und die gleiche Länge haben.

Im Beispiel erreicht man das näherungsweise mit der Ränderung

$\underline {A}:={\begin{pmatrix}1&10&\underline {0}\\0&1&\underline {10}\\\underline {10}&\underline {0}&\underline {0}\end{pmatrix}}.$

Die Lage der Spaltenvektoren der geränderten Matrix $\underline {A}$ im $\mathbb {R} ^{3}$ ist im folgenden Bild veranschaulicht.

Für das geränderte System

$\underline A\underline x=\underline b$

ergeben sich mit den geränderten rechten Seiten $\underline b^{{(1)}}=(1,0,0)$ und $\underline b^{{(2)}}=(1,0.1,0)$ jeweils die Lösungen $\underline x^{{(1)}}=(0,0.1,-0.01)$ bzw. $\underline x^{{(2)}}=(0,0.1,0)$ . Die für die Messaufgabe wesentlichen Komponenten $x_{1}$ und $x_{2}$ ändern sich also durch die 10 %ige Störung von überhaupt nicht.

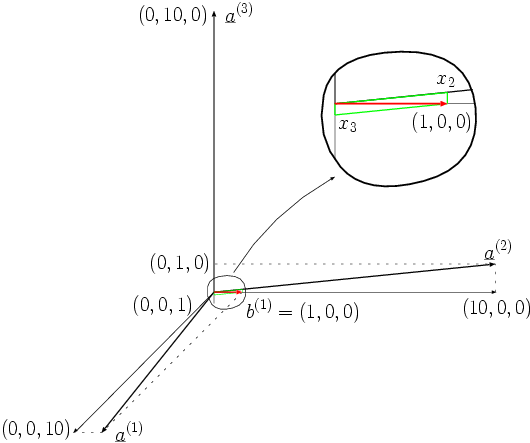
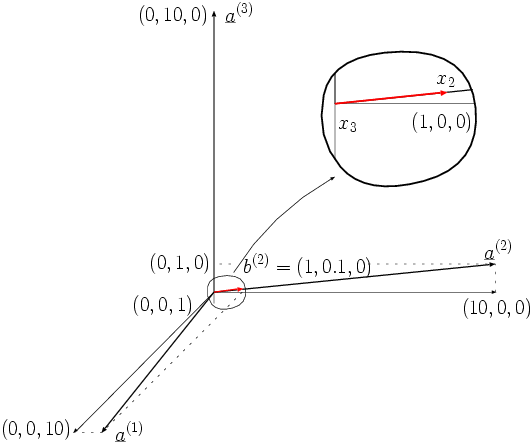
Das ist in den folgenden zwei Bildern noch einmal veranschaulicht.

Die Konditionszahl der geränderten Matrix hat sich auf $\operatorname {cond}(\underline A)\approx 1.15$ verringert. Der relative Fehler wird sich durch die Berechnung von ${\underline {x}}$ aus den Messwerten $\underline b$ also nur noch höchstens um ca. 15 % verschlechtern.

In diesem motivierenden Beispiel wurde die Ränderung sehr einfach gehalten. Durch eine geschicktere Wahl der Ränderung ist erreichbar, dass sich der relative Fehler durch die Berechnung von aus überhaupt nicht mehr verschlechtert, dass also $\operatorname {cond}(\underline A)=1$ gilt.

Regularisierung

Sei eine reelle $m\times n$ -Matrix und ein dazu passender -dimensionaler Spaltenvektor. Eine geränderte Matrix

$\left({\begin{matrix}A&A_{{{\rm {ro}}}}\\A_{{{\rm {lu}}}}&0\end{matrix}}\right)$

mit passenden Matrizen $A_{{{\rm {ro}}}}$ und $A_{{{\rm {lu}}}}$ ist genau dann regulär, wenn die Zeilen von $A_{{{\rm {lu}}}}$ eine Basis des Kerns von bilden und die Spalten von $A_{{{\rm {ro}}}}$ ein minimales System von Spalten ist, das zusammen mit den Spalten von den $\mathbb{R}^m$ aufspannt. In diesem Fall lässt sich das geränderte System

$\left({\begin{matrix}A&A_{{{\rm {ro}}}}\\A_{{{\rm {lu}}}}&0\end{matrix}}\right)\left({\begin{matrix}x\\x_{{u}}\end{matrix}}\right)=\left({\begin{matrix}b\\0\end{matrix}}\right)$

eindeutig lösen und die Dimension der (quadratischen) geränderten Matrix ist $m+\operatorname {def}(A)$ (hierbei ist $\operatorname {def}(A)$ der Defekt von ).

Je nach Wahl der Matrizen $A_{{{\rm {ro}}}}$ und $A_{{{\rm {lu}}}}$ kann man verschiedene Aufgaben lösen. Spannen zum Beispiel die Zeilen von $A_{{{\rm {lu}}}}$ den Kern von auf und die Spalten von $A_{{{\rm {ro}}}}$ das orthogonale Komplement des Bildes von , so ist aus der Lösung des geränderten Gleichungssystems gerade $A^{+}b$ mit der Pseudoinversen A^+ von . Den Kern von kann man mit Hilfe des Gaußschen Eliminationsverfahrens berechnen und das orthogonale Komplement des Bildes von berechnet man günstigerweise als Kern von $A^{T}$ .

Optimale Ränderung

Die Idee aus dem letzten Abschnitt wird hier aufgegriffen und eine beliebige Matrix $A\in {\mathbb {R}}^{{m\times n}}$ so gerändert, dass die Spalten der erweiterten Matrix ${\overline {A}}$ alle senkrecht aufeinander stehen und die gleiche euklidische Norm haben. Die erweiterte Matrix ${\bar {A}}$ ist dann das Produkt des größten Singulärwertes von mit einer orthogonalen Matrix und hat damit die minimal mögliche Konditionszahl eins.

Singulärwertzerlegung als Hilfsmittel zur Ränderung

Die Struktur der Systemmatrix kann man mit Hilfe einer aus der Singulärwertzerlegung $A=U\Sigma V^{T}$ von $A\in {\mathbb {R}}^{{m\times n}}$ gewonnenen Koordinatentransformation $b_{U}:=U^{T}b$ , $x_{V}:=V^{T}x$ vereinfachen. Die neue Systemmatrix $\Sigma \in {\mathbb {R}}^{{m\times n}}$ hat dann sehr viele Nulleinträge. Nur die Elemente $\Sigma _{{1,1}},\ldots ,\Sigma _{{r,r}}$ sind mit Nichtnullelementen, nämlich den Singulärwerten $\Sigma _{{1,1}}:=\sigma _{1}\geq \Sigma _{{2,2}}:=\sigma _{2}\ldots \geq \Sigma _{{r,r}}:=\sigma _{r}>0$ , belegt. Hierbei ist der Rang der Matrix .

Die Transformationsmatrizen $U\in {\mathbb {R}}^{{m\times m}}$ und $V\in {\mathbb {R}}^{{n\times n}}$ sind orthogonal und damit normerhaltend $|b_{U}|=|U^{T}b|$ , $|x_{V}|=|V^{T}x|$ . Daraus folgt, dass die transformierte Systemmatrix $\Sigma$ die gleiche Kondition hat, wie die originale Systemmatrix .

Eine Erweiterung

${\bar \Sigma }:={\begin{pmatrix}\Sigma &{\bar \Sigma }_{{{\rm {{ro}}}}}\\{\bar \Sigma }_{{{\rm {{lu}}}}}&{\bar \Sigma }_{{{\rm {{ru}}}}}\end{pmatrix}}\in {\mathbb {R}}^{{{\bar m}\times {\bar n}}}\qquad {\mbox{ mit }}{\bar m}\geq m{\mbox{ und }}{\bar n}\geq n$

der Matrix $\Sigma$ um Matrixblöcke (zueinander passender Dimensionen) ${\bar \Sigma }_{{{\rm {{ro}}}}}\in {\mathbb {R}}^{{{\bar m}\times ({\bar n}-n)}},{\bar \Sigma }_{{{\rm {{lu}}}}}\in {\mathbb {R}}^{{({\bar m}-m)\times n}},{\bar \Sigma }_{{{\rm {ru}}}}^{{({\bar m}-m)\times ({\bar n}-n)}}$ entspricht eine Ränderung der Matrix , wenn man die Transformationsmatrizen und passend durch Teile der Einheitsmatrix ergänzt:

${\bar {A}}:={\begin{pmatrix}U&{\mathbf {0}}_{{m\times ({\bar m}-m)}}\\{\mathbf {0}}_{{({\bar m}-m)\times m}}&{\mathbf {1}}_{{({\bar m}-m)\times ({\bar m}-m)}}\end{pmatrix}}{\begin{pmatrix}\Sigma ^{{(11)}}&{\bar \Sigma }_{{{\mathrm {ro}}}}\\{\bar \Sigma }_{{{\mathrm {lu}}}}&{\bar \Sigma }_{{{\mathrm {ru}}}}\end{pmatrix}}{\begin{pmatrix}V^{T}&{\mathbf {0}}_{{n\times ({\bar n}-n)}}\\{\mathbf {0}}_{{({\bar n}-n)\times n}}&{\mathbf {1}}_{{({\bar n}-n)\times ({\bar n}-n)}}\end{pmatrix}}={\begin{pmatrix}U\Sigma V^{T}&U{\bar \Sigma }_{{{\mathrm {ro}}}}\\{\bar \Sigma }_{{{\mathrm {lu}}}}V^{T}&{\bar \Sigma }_{{{\mathrm {ru}}}}\end{pmatrix}}={\begin{pmatrix}A&U{\bar \Sigma }_{{{\mathrm {ro}}}}\\{\bar \Sigma }_{{{\mathrm {lu}}}}V^{T}&{\bar \Sigma }_{{{\mathrm {ru}}}}\end{pmatrix}}$

Die erweiterten Transformationsmatrizen ${\bar V}:={\begin{pmatrix}V&{\mathbf {0}}\\{\mathbf {0}}&{\mathbf {1}}\end{pmatrix}}$ und ${\bar U}:={\begin{pmatrix}U&{\mathbf {0}}\\{\mathbf {0}}&{\mathbf {1}}\end{pmatrix}}$ sind wieder orthogonal, womit die Kondition der erweiterten Systemmatrix ${\bar {A}}$ mit der der Matrix ${\bar \Sigma }$ übereinstimmt.

Im Folgenden brauchen also nur noch Matrizen untersucht werden, die eine Systemmatrix mit der (von der Singulärwertzerlegung her bekannten) Struktur

$\Sigma _{{i,j}}=\left\{{\begin{matrix}\sigma _{{i,i}}&{\mbox{ wenn }}&i=j\leq r\\0&{\mbox{ sonst }}\end{matrix}}\right.$

mit einer ganzen Zahl $0\leq r\leq \min(m,n)$ haben.

Ergänzung einer rechteckigen Matrix zu einer quadratischen

Hier wird nur die Ränderung von Matrizen mit mehr Zeilen als Spalten beschrieben ( m>n ). Durch Transposition kann man die Aussagen auf Matrizen mit mehr Spalten als Zeilen übertragen. Mit den Aussagen aus dem vorhergehenden Abschnitt ist klar, dass man sich auf die Untersuchung von Matrizen der Form

$\Sigma =\left({\begin{matrix}D\\{\mathbf {0}}\end{matrix}}\right)$

beschränken kann, wobei eine positiv semidefinite Diagonalmatrix und $\mathbf {0}$ eine Nullmatrix mit der gleichen Anzahl an Spalten wie ist. Zunächst wird vorausgesetzt, dass keine Nullmatrix ist. Das maximale Diagonalelement $d_{\max }$ von ist also größer null. Dann ist es günstig, die fehlenden Spalten durch die an diese Spaltenpositionen gehörigen Spalten der mit $d_{\max }$ skalierten Einheitsmatrix zu ergänzen:

${\bar \Sigma }=\left({\begin{matrix}D&{\mathbf {0}}\\{\mathbf {0}}&d_{\max }{\mathbf {1}}\end{matrix}}\right).$

Falls regulär ist, trifft das auch für die geränderte Matrix ${\bar \Sigma }$ zu. Man hat also die Matrix in diesem Falle regularisiert.

Nachdem man die Rechteckmatrix so zu einer quadratischen ergänzt hat, kann man die im nächsten Abschnitt beschriebene Ränderung benutzen, um die Matrix besser zu konditionieren (oder, falls singulär ist, zu regularisieren). Dort wird sich herausstellen, dass die Wahl von $d_{\max }$ als Skalierungsfaktor günstig ist, da man die Norm dieser Spalten dann nicht mehr künstlich durch eine Ränderung vergrößern muss.

Optimale Ränderung einer quadratischen Matrix

Im vorhergehenden Abschnitt wurde beschrieben, wie man eine rechteckige Matrix durch Ränderung günstig zu einer quadratischen ergänzen kann. Hier wird nun darauf eingegangen, wie sich die Kondition einer quadratischen Matrix verbessern oder im singulären Fall die Matrix regularisieren lässt.

Der Unterabschnitt zur Singulärwertzerlegung zeigt, dass man sich dabei auf die Ränderung von Diagonalmatrizen $\Sigma =\operatorname {diag}(\sigma _{1},\ldots ,\sigma _{r},0\ldots ,0)$ beschränken kann.

Die Spaltenvektoren der Matrix $\Sigma$ stehen bereits senkrecht aufeinander. Man muss sie nur noch geeignet verlängern, damit sie normgleich werden. Dabei fängt man mit dem letzten Spaltenvektor an, dessen Komponente $\Sigma _{{n,n}}$ den kleinsten Wert der Diagonalelemente von $\Sigma$ hat. Zunächst ergänzt man $\Sigma$ durch eine Zeile $z_{{n+1,\bullet }}:=(0\;\ldots \;0\;z_{{n+1,n}})\in {\mathbb {R}}^{{1\times n}}$ , was einer Erweiterung des Spaltenvektorraumes um eine Dimension entspricht (der Punkt ${}_{\bullet }$ steht hier als Stellvertreter für den Spaltenindex). In dieser zusätzlichen Dimension verlängert man den letzten Spaltenvektor der erweiterten Matrix so weit, dass er die gleiche euklidische Länge wie der erste (längste) Spaltenvektor von $\Sigma$ bekommt (also die Länge $\sigma _{1}$ ):

$z_{{n+1,n}}:={\sqrt {\sigma _{1}^{2}-\Sigma _{{n,n}}^{2}}}.$

Die Spaltenvektoren der erweiterten Matrix $\left({\begin{matrix}\Sigma \\z_{{n+1,\bullet }}\end{matrix}}\right)$ bleiben dadurch orthogonal zueinander. Um wieder eine quadratische Matrix zu erhalten, muss man noch eine Spalte $s_{{\bullet ,n+1}}$ ergänzen. Dazu wählt man günstigerweise eine Spalte mit

$s_{{i,n}}:=\left\{{\begin{matrix}z_{{n+1,n}}&{\mbox{ wenn }}&i=n\\-\Sigma _{{n,n}}&{\mbox{ wenn }}&i=n+1\\0&{\mbox{ sonst}}&\end{matrix}}\right.$

Die Spalte $s_{{\bullet ,n+1}}$ hat die gewünschte Norm $\sigma _{1}$ und steht wiederum senkrecht auf allen anderen Spalten der erweiterten Matrix

${\bar \Sigma }:=\left({\begin{matrix}\left.{\begin{matrix}\Sigma \\\overline {z_{{n+1,\bullet }}}\end{matrix}}\right|&s_{{\bullet ,n+1}}\end{matrix}}\right)$ .

Durch analoges Ergänzen weiterer Zeilen und Spalten kann man sukzessive die Norm aller Spaltenvektoren der erweiterten Matrix angleichen. Wie gewünscht, ist das Ergebnis eine Systemmatrix, deren Spalten alle orthogonal aufeinander stehen und die gleiche Norm haben.

Basierend auf einem Artikel in:

Wikipedia.de