Henkelzerlegung
In der Differentialtopologie, einem Teilgebiet der Mathematik, ist die Henkelzerlegung die Grundlage für die Klassifikation und Beschreibung von Mannigfaltigkeiten.
Definition: Ankleben eines Henkels

Notation: bezeichne die
-dimensionale
Vollkugel,
die
-dimensionale
Sphäre.
Im Folgenden bezeichnen wir als
-Henkel
einer
-dimensionalen
Mannigfaltigkeit das Produkt
mit der durch die Produktstruktur gegebenen Zerlegung
.
wird als Kern und
als Kokern des Henkels bezeichnet.
Nun sei
eine
-dimensionale
differenzierbare Mannigfaltigkeit mit Rand. Das Ergebnis des
Anklebens eines
-Henkels
ist die Mannigfaltigkeit
- mit der Äquivalenzrelation
erzeugt durch
für alle
,
für eine Einbettung
.
Durch kanonisches Glätten der Ecken erhält man eine differenzierbare Mannigfaltigkeit.[1] (Insbesondere ist das Ankleben eines
-Henkels
die disjunkte Vereinigung mit einem
-Ball
).
Die so erhaltene Mannigfaltigkeit ist eindeutig bestimmt durch die Einbettung
oder äquivalent durch eine
gerahmte Einbettung
.
Die Sphäre heißt die Anklebesphäre und die Sphäre
heißt die Gürtelsphäre.
Henkelzerlegung
Jede kompakte differenzierbare Mannigfaltigkeit besitzt eine Henkelzerlegung.
Der Beweis dieses Satzes benutzt Morse-Theorie. Zu jeder differenzierteren Mannigfaltigkeit
gibt es eine Morse-Funktion
, deren kritische Punkte unterschiedlichen Funktionswerten entsprechen (und nicht auf dem Rand liegen). Der Satz
folgt dann mittels vollständiger Induktion aus folgender lokalen Beschreibung der Umgebung eines kritischen Punktes.
Es sei eine
-Funktion
mit genau einem kritischen Punkt in
und keinen weiteren kritischen Punkten in
(für ein geeignetes
). Dann entsteht
aus
durch Ankleben eines
-Henkels,
wobei
der Index des kritischen Punktes in
ist.
Dieser Satz geht auf Stephen Smale zurück, der 1961 einen Beweis skizzierte und die
Henkel-Zerlegung dann zum Beweis der Poincaré-Vermutung in Dimensionen
benutzte.[2] John Milnor
bewies in seinem Buch „Morse Theory“ eine schwächere Version, die besagt, dass
homotopieäquivalent zu dem aus
durch Ankleben einer k-Zelle entstehenden Raum
ist.[3] Ein vollständiger Beweis wurde 1963 von Palais gegeben.[4]
vereinfachte Fassungen finden sich bei Fukui[5] und Madsen-Tornehave.[6]
Niedrigdimensionale Beispiele
- Klassifikation der Flächen: Jede geschlossene,
orientierbare Fläche besitzt eine Henkelzerlegung aus einem 0-Henkel,
1-Henkeln und einem 2-Henkel. Die Zahl
ist das Geschlecht der Fläche.
- Heegaard-Zerlegung von 3-Mannigfaltigkeiten: Ein (3-dimensionaler) Henkelkörper
vom Geschlecht
entsteht durch Ankleben von
1-Henkeln an einen 0-Henkel. Als Heegaard-Zerlegung bezeichnet man die Zerlegung einer 3-Mannigfaltigkeit in zwei Henkelkörper. Jede geschlossene, orientierbare 3-Mannigfaltigkeit besitzt eine Heegaard-Zerlegung, das minimal mögliche
wird als Heegaard-Geschlecht bezeichnet. Eine Heegaard-Zerlegung bestimmt eine Henkelzerlegung der 3-Mannigfaltigkeit in einen 0-Henkel,
1-Henkel,
2-Henkel und einen 3-Henkel.
- Kirby-Kalkül: Henkelzerlegungen 4-dimensionaler Mannigfaltigkeiten werden durch Kirby-Diagramm beschrieben.
Relative Henkelzerlegung
Es sei
eine kompakte, differenzierbare Mannigfaltigkeit mit einer Zerlegung des Randes
in (möglicherweise leere) Teilmengen
.
Eine Henkelzerlegung von relativ zu
ist eine Darstellung von
als durch sukzessives Ankleben von Henkeln an
konstruierte Mannigfaltigkeit. Mittels Morse-Theorie kann man zeigen, dass es zu jedem solchen Paar
eine Henkelzerlegung von
relativ zu
gibt.[7]
Cerf-Theorie
Zwei Henkelzerlegungen derselben Mannigfaltigkeit lassen sich durch Henkelgleiten (engl.: handle slide) und Hinzufūgen oder Weglassen zweier komplementärer Henkel (engl.: cancellation) ineinander überführen.
Henkelgleiten
Die Mannigfaltigkeit entstehe aus
durch Ankleben eines
-Henkels
mittels der Anklebe-Abbildung
.
Es sei
eine Isotopie mit
und
.
Dann ist die durch Ankleben eines
-Henkels an
mittels der Verklebeabbildung
konstruierte Mannigfaltigkeit
diffeomorph zu
.
Insbesondere kann man einen
-Henkel
stets so ankleben, dass seine Anklebesphäre disjunkt von den Gürtelsphären aller
-Henkel mit
ist.
Als Folgerung daraus kann man für jede kompakte, differenzierbare Mannigfaltigkeit eine Henkelzerlegung so konstruieren, dass Henkel in aufsteigender Folge ihrer Indizes an eine
Menge von
-Henkeln
angeklebt werden, d. h. für
werden die
-Henkel
nach den
-Henkeln
angeklebt.
Komplementäre Henkel
Ein -Henkel
und ein
-Henkel
heißen komplementär, wenn die Anklebesphäre des
-Henkels
die Gürtelsphäre des
-Henkels
in genau einem Punkt transversal schneidet.
Wenn eine Mannigfaltigkeit aus einer Mannigfaltigkeit
durch Ankleben eines
-Henkels
und anschließendes Ankleben eines zu diesem komplementären
-Henkels
entsteht, dann ist
diffeomorph zu
.
Als Folgerung daraus kann man eine Henkel-Zerlegung stets so wählen, dass es genau einen 0-Henkel gibt und weiterhin, falls
bzw.
so dass es genau einen bzw. keinen
-Henkel mit
gibt.
Satz von Cerf
Zwei (relative) Henkelzerlegungen eines Paares
(mit in aufsteigender Reihenfolge der Indizes angeklebten Henkeln) lassen sich durch eine Folge von Henkel-Gleiten, Hinzufügen/Entfernen
eines komplementären Henkelpaares und Isotopien ineinander überführen.[8]
Chirurgien (Sphärische Modifikationen) und Zusammenhang zur Kobordismustheorie
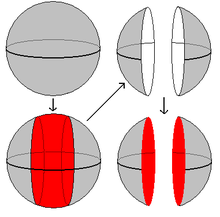
Wenn eine Mannigfaltigkeit
aus
durch Ankleben eines
-Henkels
entsteht, dann entsteht die (m-1)-Mannigfaltigkeit
aus
durch eine
-Chirurgie, d. h. durch Ausschneiden der eingebetteten
und anschließendes Einkleben von
mittels der kanonischen Identifikation
.
(Diese Chirurgien werden in der Literatur auch als sphärische Modifikationen bezeichnet.)
Sei
ein Kobordismus zwischen geschlossenen Mannigfaltigkeiten
und
,
also eine kompakte Mannigfaltigkeit
mit
. Dann erhält man mit dem Satz von Smale eine Henkelzerlegung von
relativ zu
und mithin eine Konstruktion von
aus
durch eine Abfolge von Chirurgien (sphärischen Modifikationen).
Literatur
- Robert E. Gompf, András I. Stipsicz: 4-manifolds and Kirby calculus (= Graduate Studies in Mathematics. 20). American Mathematical Society, Providence RI 1999, ISBN 0-8218-0994-6.
- Yukio Matsumoto: An introduction to Morse theory (= Translations of Mathematical Monographs. 208 = Iwanami Series in Modern Mathematics.). Translated from the 1997 Japanese original by Kiki Hudson and Masahico Saito. American Mathematical Society, Providence RI 2002, ISBN 0-8218-1022-7.
Einzelnachweise
- ↑ Stephen Smale: On the structure of 5-manifolds. In: Annals of Mathematics. Band 75, Nummer 1, 1962,
S. 38–46, JSTOR:
 1970417.
1970417.
- ↑ Stephen Smale: Generalized Poincaré’s conjecture in dimensions greater than four. In: Annals of
Mathematics. Band 74, Nummer 2, 1961, S. 391–406, JSTOR:
 1970239.
1970239.
- ↑ John Milnor: Morse theory. Based on lecture notes by M. Spivak and R. Wells (= Annals of Mathematics Studies. 51). Princeton University Press, Princeton NJ 1963.
- ↑ Richard S. Palais: Morse theory on Hilbert manifolds. In: Topology. Band 2, Nummer 4, 1963,
S. 299–340,
doi:
 10.1016/0040-9383(63)90013-2.
10.1016/0040-9383(63)90013-2.
- ↑ Takehiro Fukui: On a proof of theorem in passing a critical level. In: Mathematical Seminar Notes. Kobe University. Band 3, 1975, S. 71–74.
- ↑ Ib Madsen, Jørgen Tornehave: From Calculus to Cohomology. De Rham cohomology and characteristic classes. Cambridge University Press, Cambridge u. a. 1997, ISBN 0-521-58059-5 (Appendix C).
- ↑ John Milnor: Lectures on the h-Cobordism Theorem. Notes by Laurent Siebenmann and Jonathan Sondow. Princeton University Press, Princeton NJ 1965.
- ↑ Jean Cerf: La stratification naturelle des espaces de fonctions différentiables réelles et le théorème de la pseudo-isotopie. In: Publications Mathématiques de l’IHÉS. Band 39, 1970, S. 5–173.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.02. 2025