
Quadratwurzel aus 3
 |
 | |
|
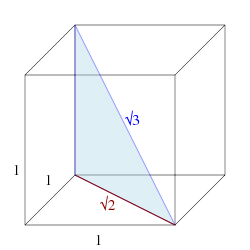
Wurzel 3 als Länge der Diagonale eines
Würfels |
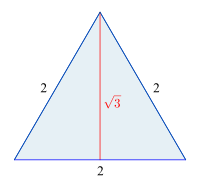
Wurzel 3 als Länge der Höhe eines gleichseitigen
Dreiecks |
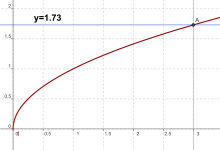
Die Quadratwurzel aus 3 (geschrieben )
ist die positive, reelle
Zahl, die mit sich selbst multipliziert 3 ergibt. Die Wurzel von 3 ist eine
irrationale
Zahl. Sie ist eine mathematische
Konstante, auch bekannt unter dem Namen Theodorus-Konstante, benannt
nach Theodoros
von Kyrene.
Näherungsweise gilt:
Ihre Kettenbruchentwicklung ist
[1;1,2,1,2,1,2,1,2,1,2,…].
Es ist auch
und
Beweis der Irrationalität
Angenommen,
wäre rational. Dann könnte man die Zahl als Bruch zweier teilerfremder ganzer
Zahlen
und
schreiben:
.
Durch Quadrieren der Gleichung erhält man
daraus folgt
Aber dann ist für eine ganze Zahl
Daraus folgt wieder
,
also
Aber dann ist auch für eine ganze Zahl
,
was einen Widerspruch bedeutet, weil
und
teilerfremd sind.
Nachkommastellen
Die ersten 100 Nachkommastellen:
1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485756
Weitere Dezimalstellen finden sich auch unter Folge ![]() A002194 in OEIS.
A002194 in OEIS.
Der derzeitige Weltrekord der Berechnung der Nachkommastellen (vom 9. Juni 2019) liegt bei 2.000.000.000.000 und wurde von Hiroyuki Oodaira (大平 寛之) erzielt.
Anwendung
- Das Verhältnis zwischen der Diagonale eines dreidimensionalen Würfels und
der Kantenlänge beträgt
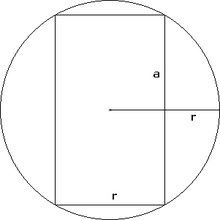
- Die Distanz zwischen zwei gegenüberliegenden Seiten eines regulären Sechsecks
mit der Seitenlänge a beträgt
, oder anders gesagt, das Doppelte des Inkreisradius
- Der Verkettungsfaktor,
das Verhältnis von Phasenspannung (230 V)
zu Außenleiterspannung (400 V), beträgt bei Dreiphasenwechselstrom
- Die Höhe eines gleichseitigen
Dreiecks mit der Seitenlänge a beträgt
, sein Flächeninhalt


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.11. 2024