Drehspiegelgruppe

Die Drehspiegelgruppe
ist die von der Drehspiegelung
zum Drehwinkel
erzeugte
Symmetriegruppe. Wird
als Grundoperation statt der Drehspiegelung die Drehinversion, also die
Verkettung der Drehung mit einer Inversion
an einem Punkt auf der Drehachse, genommen, entsteht die Gruppe
;
die an sich naheliegende Bezeichnung „Drehinversionsgruppe“ ist
ungebräuchlich.
Die Gruppen dieser beiden Typen stimmen bis auf die Nummerierung miteinander
überein. Drehspiegelgruppen treten bei der Beschreibung der Symmetrie von
Kristallen oder einzelner Moleküle auf. In der Kristallographie
sind nur die fünf Gruppen zu
=
1, 2, 3, 4 und 6 relevant, da nur diese mit der Symmetrie eines unendlich
ausgedehnten Gitters vereinbar sind. Sie gehören zu den 32 kristallographischen
Punktgruppen. Bei der Untersuchung der molekularen
Symmetrie sind auch andere Gruppen wichtig. So gibt es eine angeregte Form
des Anions [Re2Cl8]2− mit
-Symmetrie.
Die hier behandelte Symmetriegruppe
darf nicht mit der Symmetrischen
Gruppe
verwechselt werden.
Notation
Für die Drehspiegelgruppen
gibt es zwei Bezeichnungssysteme: Die hauptsächlich in der Kristallographie
verwendete Hermann-Mauguin-Symbolik,
die bei der Nummerierung auf der Drehinversion als Grundoperation basiert, sowie
die in der Chemie und Molekülphysik übliche Schoenflies-Symbolik.
| Hermann-Mauguin | |||||
| Schoenflies |
Dabei steht „m“ für „mirror plane“, „s“ für „Spiegelebene“, „i“ für
„Inversion“, „h“ für „horizontale Spiegelebene“ (bei vertikal gedachter
Drehachse) sowie „“
für eine n-zählige Drehsymmetrie („C“ für „cyclisch“); siehe hierzu den Abschnitt
„Eigenschaften“.
Beispiele
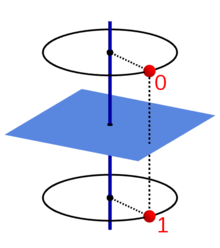
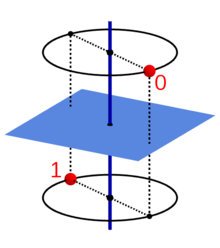
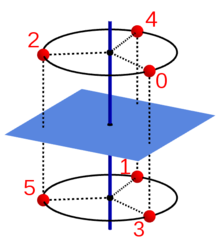
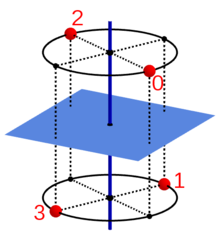
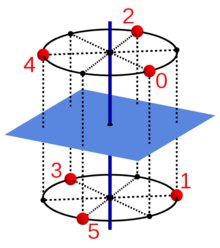
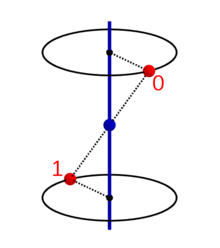
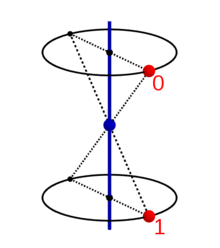
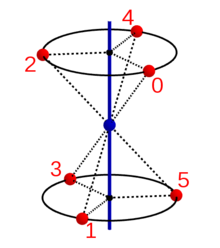
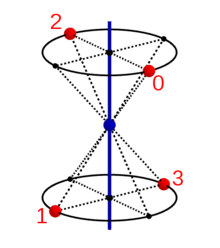
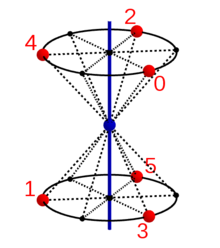
Ein Punkt in der Position 0 wird durch wiederholte Anwendung der
Grundoperation
(Drehspiegelung beziehungsweise Drehinversion) nacheinander in die Positionen 1,
2, … und schließlich wieder in die Ausgangsposition 0 überführt. Die
untenstehenden Abbildungen zeigen diese Anwendung der Gruppenelemente
auf den Punkt 0 für einige Werte von
.
 |
 |
 |
 |
 | |
 |
 |
> |
 |
 |
Ein Körper mit einer -
oder
-Symmetrie,
der den Punkt 0 enthält, muss auch die zu diesem symmetrischen Punkte 1, 2, …
enthalten. Ein Beispiel ist das oben gezeigte Antiprisma, bei dem die 4-zählige
Drehspiegelachse senkrecht auf den beiden Deckflächen steht, wobei diese hier
unterschiedlich orientiert
sind. Bei gleicher Orientierung wäre der Körper nicht mehr drehspiegel- dafür
aber weiterhin drehsymmetrisch, und zwar um nun drei 2-zählige Achsen (senkrecht
zu den Deckflächen sowie parallel zu deren Winkelhalbierenden). Bei nicht
orientierten Deckflächen würden beide Symmetrien gleichzeitig auftreten.
Eigenschaften
Die Drehspiegelgruppe
ist zyklisch
mit der Ordnung
(für ungerades
)
oder
(für gerades
).
Sie ist damit insbesondere kommutativ.
enthält die Spiegelung genau dann, wenn
ungerade ist, und die Inversion genau dann, wenn
gerade, aber nicht durch 4 teilbar ist.
hat als Untergruppen nur
Drehgruppen und Drehspiegelgruppen, und zwar ist
- die Drehgruppe
Untergruppe genau dann, wenn
Teiler von
(für ungerades
) beziehungsweise von
(für gerades
) ist;
- die Drehspiegelgruppe
Untergruppe genau dann, wenn
ungerade ist.
Zwischen den
und den Drehspiegelgruppen besteht die Beziehung


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.06. 2021