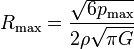Hydrostatischer Druck
Der Hydrostatische Druck (griech. ὕδωρ hýdor, Wasser), auch Gravitationsdruck oder Schweredruck, ist der Druck, der sich innerhalb eines ruhenden Fluids, das ist eine Flüssigkeit oder ein Gas, durch den Einfluss der Gravitation einstellt. Der Begriff wird entgegen der Wortbedeutung „Wasser“ auch für andere Flüssigkeiten und sogar für Gase verwendet. Dynamischer Druck durch Fluidströmungen wie z.B. der Staudruck wird vom hydrostatischen Druck nicht erfasst, er betrachtet nur ruhende, statische Fluide.
Inkompressible Flüssigkeiten im homogenen Schwerefeld
Pascal’sches Gesetz
.png)
Der Hydrostatische Druck für Fluide mit konstanter Dichte im homogenen Schwerefeld (= Inkompressible Fluide, insbesondere Flüssigkeiten) berechnet sich nach dem Pascal'schen (oder pascalschen) Gesetz (benannt nach Blaise Pascal):
Formelzeichen:
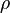 = Dichte [für Wasser: ρ ≈
1.000 kg/m³]
= Dichte [für Wasser: ρ ≈
1.000 kg/m³]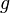 = Erdbeschleunigung
[für Deutschland: g ≈ 9,81 m/s²]
= Erdbeschleunigung
[für Deutschland: g ≈ 9,81 m/s²]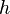 = Höhe (hier: des Flüssigkeitsspiegels)
= Höhe (hier: des Flüssigkeitsspiegels)
⇒ 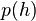 = Hydrostatischer Druck (p) in Abhängigkeit von der Höhe (h)
des Flüssigkeitsspiegels.
= Hydrostatischer Druck (p) in Abhängigkeit von der Höhe (h)
des Flüssigkeitsspiegels.
Einheiten
Die Physikalischen Einheiten für den Hydrostatischen Druck sind:
- international die SI-Einheit
- zudem in Deutschland und Österreich die „gesetzliche Einheit“
-
- Bar
(
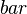 ):
1 bar = 100.000 Pa bzw. N/m² (= 100 kPa)
):
1 bar = 100.000 Pa bzw. N/m² (= 100 kPa)
- Bar
(
Zur Beschreibung des Hydrostatischen Drucks wird zum Teil auch noch die
nicht-SI-konforme
veraltete Maßeinheit Meter
Wassersäule (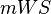 )
verwendet.
)
verwendet.
Beispiel zum Hydrostatischen Paradoxon
- Bsp.: Wassersäule, Höhe: 50 Meter:
-
- 50 m × 1.000 kg/m³ × 9,81 m/s² ≈ 490.500 N/m² ≈ 4,90 bar
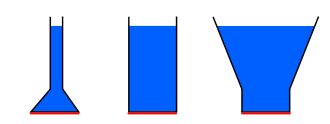
Der Hydrostatische Druck hängt also nicht von der Form eines Gefäßes ab; entscheidend für den Druck an dessen Boden ist alleine die Höhe des Fluid- bzw. Flüssigkeitsspiegels und nicht die absolute Menge des Fluids im Gefäß. Dieses Phänomen wurde als Hydrostatisches (oder auch Pascal'sches) Paradoxon bekannt.
Gesamtdruck am Boden der Flüssigkeit
Zur vollständigen Beschreibung des Drucks am Boden eines ruhenden inkompressiblen Fluids ist dem Hydrostatischen Druck hinzu allerdings noch der Umgebungsdruck zu addieren. So entspricht beispielsweise der auf einen Taucher wirkende Wasserdruck in einem ruhenden Gewässer der Summe
- aus dem Luftdruck, der auf die Gewässeroberfläche wirkt, + dem Hydrostatischen Druck des Wassers selbst.
Gravitationsdruck in Planeten, Monden, Asteroiden und Meteoriten
Tiefenabhängigkeit von g
Mit zunehmender Tiefe kann g nicht mehr als konstant betrachtet werden. Wenn die Form des Himmelskörpers durch eine Kugel mit Radius R beschrieben und die Dichte als konstant betrachtet wird, lässt sich der Druck wie folgt berechnen:
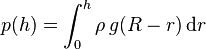 .
.
Der Ortsfaktor 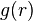 folgt aus dem Newtonschen
Gravitationsgesetz :
folgt aus dem Newtonschen
Gravitationsgesetz :
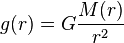 ,
,
wobei 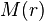 die Masse innerhalb einer konzentrischen Kugel innerhalb des Himmelskörpers und
die Masse innerhalb einer konzentrischen Kugel innerhalb des Himmelskörpers und
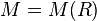 dessen Gesamtmasse angibt. Mit der Formel für das Kugelvolumen
dessen Gesamtmasse angibt. Mit der Formel für das Kugelvolumen 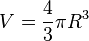 ergibt sich für den Druck im Zentrum:
ergibt sich für den Druck im Zentrum:
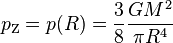 .
.
Begrenzung der Größe eines Himmelskörpers aufgrund der Druckfestigkeit
Verschiedene Materialien weisen eine unterschiedliche Druckfestigkeit auf.
Das Gleichsetzen von 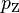 und dem Maximaldruck
und dem Maximaldruck 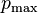 führt zu einer Gleichung, die sich nach
führt zu einer Gleichung, die sich nach 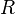 auflösen lässt. Der resultierende Wert
auflösen lässt. Der resultierende Wert
gibt den maximalen Radius an, den ein homogener, kugelförmiger Himmelskörper besitzen darf, um die Druckfestigkeit des Materials nicht zu überschreiten, also um nicht von der eigenen Masse zerdrückt zu werden.
Maximale Radien für verschiedene Materialien
Für den sehr hypothetischen Fall eines vollständig aus Styropor bestehenden
Himmelskörper (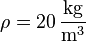 und
und 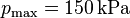 )
würde sich ein Radius von rund
)
würde sich ein Radius von rund 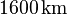 ergeben (zum Vergleich: der Radius des Erdmondes beträgt rund
ergeben (zum Vergleich: der Radius des Erdmondes beträgt rund 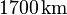 ).
Für Granit beträgt der Radius rund
).
Für Granit beträgt der Radius rund 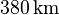 und für Basalt
und für Basalt 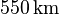 . Eine Schlussfolgerung ist, dass Himmelskörper mit einem Radius deutlich größer
dem der Erde nicht aus einem einzigen festen Material bestehen können (Diamant:
. Eine Schlussfolgerung ist, dass Himmelskörper mit einem Radius deutlich größer
dem der Erde nicht aus einem einzigen festen Material bestehen können (Diamant:
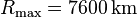 )
.
)
.
Gravitationsdruck in Sternen
Sterne im Gleichgewicht
Einen Spezialfall des hydrostatischen Drucks stellt der Gravitationsdruck in Sternen dar. Dieser resultiert aus der den Stern kontrahierenden Schwerkraft. Demgegenüber wirkt z.B. der Strahlungsdruck als den Stern expandierende Kraft. Bei einem stabilen Stern stellt sich dabei ein Gleichgewicht aller Kräfte ein und der Stern hat eine stabile Form. Dies ist näherungsweise der Zustand von Sternen auf der Hauptreihe.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.11. 2019
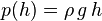
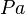 ):
1 Pa = 1
):
1 Pa = 1