Halteproblem

Das Halteproblem beschreibt eine Frage aus der theoretischen Informatik.

Wenn für eine Berechnung mehrere Rechenschritte nach festen Regeln durchgeführt werden, entsteht eine Berechnungsvorschrift, ein sogenannter Algorithmus. Zur Ausführung von Algorithmen benutzt man in der theoretischen Informatik abstrakte Maschinen. Eine typische abstrakte Maschine ist die Turingmaschine.

Das Halteproblem beschreibt die Frage, ob die Ausführung eines Algorithmus zu einem Ende gelangt. Obwohl das für viele Algorithmen leicht beantwortet werden kann, konnte der Mathematiker Alan Turing beweisen, dass es keinen Algorithmus gibt, der diese Frage für alle möglichen Algorithmen und beliebige Eingaben beantwortet. Diesen Beweis vollzog er an einer Turingmaschine.

Das Halteproblem ist somit algorithmisch nicht entscheidbar. Das Resultat spielt eine grundlegende Rolle in der Berechenbarkeitstheorie.

Der Begriff Halteproblem wurde nicht von Turing geprägt, sondern erst später durch Martin Davis in seinem Buch Computability and Unsolvability.

Bedeutung

In formalen Systemen der Mathematik gibt es beweisbare Aussagen.

Beispiel: Die Summe der Innenwinkel jedes beliebigen ebenen Dreiecks beträgt 180 Grad.

Erreichen formale Systeme einen bestimmten Grad an Komplexität, so lassen sich Aussagen angeben, die man weder beweisen noch widerlegen kann. Der Beweis dieser Eigenschaft wurde 1931 vom österreichischen Mathematiker Kurt Gödel veröffentlicht (gödelscher Unvollständigkeitssatz). Damit zeigte Gödel die Unmöglichkeit des Hilbertprogramms auf. Mit diesem wollte David Hilbert 1920 die Mathematik auf ein vollständiges und widerspruchsfreies System von Axiomen (unbewiesene Grundannahmen) gründen.

Auch nach den Erkenntnissen von Alan Turing gilt: In jedem formalen System, das Turingmaschinen enthält, lassen sich Aussagen formulieren, die weder bewiesen noch widerlegt werden können. Das Halteproblem beschreibt eine solche Aussage. Aus der Unlösbarkeit des Halteproblems folgt, dass es mathematische Funktionen gibt, die zwar wohldefiniert sind, deren Werte sich jedoch nicht für jeden Parameter berechnen lassen. Ein bekanntes Beispiel für eine solche Funktion ist die Radó-Funktion.

Die Church-Turing-These besagt, dass alles, was intuitiv berechenbar ist, auch von einer Turingmaschine berechenbar ist. Wenn diese Aussage wahr ist, kann das Halteproblem grundsätzlich nicht algorithmisch entschieden werden. Das führt zu der philosophisch weitreichenden Aussage, dass nicht jedes Problem lösbar ist, selbst dann nicht, wenn man alle relevanten Informationen kennt und sich streng an einen mathematisch überzeugenden Formalismus hält.

Aus der Nichtentscheidbarkeit des Halteproblems folgt, dass im Allgemeinen eine automatisierte Bestimmung logischer Feststellungen („dieser Sachverhalt ist wahr“ – durch eine Programmlogik – nicht möglich ist. Insbesondere ist es generell nicht möglich, automatisiert festzustellen, welche Programme jemals zu einem Ende finden (Terminierungsbeweis). Für bestimmte Klassen von Turingmaschinen ist das Halteproblem jedoch entscheidbar (zum Beispiel für Programme ohne Schleifen). Viele in der Praxis vorkommende Programme und Verfahren sind daher so strukturiert, dass auf Basis dieser Struktur ein automatisierter Terminierungsbeweis geführt werden kann.

Illustration

Bei vielen Programmen ist es leicht, festzustellen, ob sie irgendwann anhalten. Es gibt allerdings auch Programme, bei denen es nach dem gegenwärtigen Wissensstand noch nicht möglich ist, vorherzusagen, ob sie bei jeder möglichen Eingabe anhalten. Das folgende Programm hält für jede Eingabe (bei n>0 und $n\in \mathbb {N}$ ), wenn die bisher unbewiesene Collatz-Vermutung richtig ist. Die Collatz-Vermutung sagt nämlich aus, dass eine solche Schleife früher oder später immer die Zahlenfolge 4, 2, 1 hervorbringen würde, was bei der hier gegebenen Abbruchbedingung "bis n = 1" zum Halten des Programms führen würde.

wiederhole
  falls n gerade:  n := n / 2
  sonst:           n := (3 * n) + 1
bis n = 1

Mathematische Beschreibung

Problemstellung

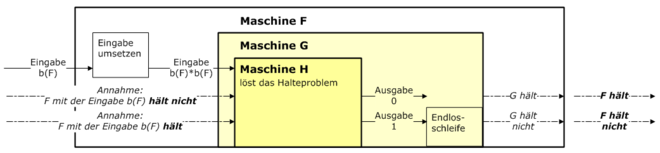
Falls das Halteproblem entscheidbar ist, gibt es eine Turingmaschine , die für jede Turingmaschine mit jeder Eingabe entscheidet, ob irgendwann anhält oder endlos weiterläuft. Die Eingabe für besteht dabei jeweils aus einer codierten Beschreibung b(T) der Maschine und deren Eingabe .

Alan Turing bewies 1937, dass eine solche Maschine nicht existiert.

Beweisidee

Das Halteproblem ist entscheidbar genau dann, wenn sowohl das Halteproblem als auch sein Komplement semientscheidbar sind. Das Halteproblem ist offensichtlich semientscheidbar: Eine universelle Turingmaschine, die als Eingabe eine Beschreibung b(T) einer Turingmaschine und eine Zeichenkette erhält, hält genau dann, wenn mit Eingabe hält. Es muss also gezeigt werden, dass das Komplement des Halteproblems nicht semientscheidbar ist, dass es also keine Turingmaschine gibt, die bei Eingabe b(T)*w immer dann 1 ausgibt, wenn mit Eingabe nicht hält.

g(i,w)	w=1	w=2	w=3	w=4	w=5	w=6
i=1	1	U	U	1	U	1
i=2	U	U	U	1	U	U
i=3	U	1	U	1	U	1
i=4	1	U	U	1	U	U
i=5	U	U	U	1	1	1
i=6	1	1	U	U	1	U

g(i,i)	1	U	U	1	1	U
f(i)	1	U	U	1	1	U

Anschauliche Darstellung der Funktionen g und f. U steht für „undefiniert“.

Dies gelingt durch ein Diagonalargument. Dafür wird zunächst angenommen, das Komplement des Halteproblems sei semientscheidbar. (Der Beweis ist also indirekt.) Anstelle einer Turingmaschine kann man auch die Funktion betrachten, die von ihr berechnet wird. Die Turingmaschine berechnet die partielle Funktion

$g(i,w)={\begin{cases}1&{\text{falls }}{\text{ die Turingmaschine }}i{\text{ bei Eingabe }}w{\text{ nicht hält}},\\{\text{undefiniert}}&{\text{sonst.}}\end{cases}}$

Die Diagonale von wird durch die folgende Funktion berechnet.

$f(i)={\begin{cases}1&{\text{falls }}{\text{ die Turingmaschine }}i{\text{ bei Eingabe }}i{\text{ nicht hält}},\\{\text{undefiniert}}&{\text{sonst.}}\end{cases}}$

Sei $n_{f}$ die Nummer einer Turingmaschine , welche die Funktion berechnet. Der Funktionswert von an der Stelle $i=n_{f}$ ist also

1, falls $f(n_{f})=g(n_{f},n_{f})=1$ , falls also bei Eingabe $n_{f}$ nicht hält. Das ist allerdings ein Widerspruch, denn berechnet und muss also halten und 1 ausgeben.
undefiniert, falls $f(n_{f})=g(n_{f},n_{f})$ undefiniert ist, falls also bei Eingabe $n_{f}$ hält. Das ist ebenfalls ein Widerspruch, denn ist an dieser Stelle undefiniert, und berechnet .

Beweisskizze

Der Beweis orientiert sich an der Konstruktion von Marvin Lee Minsky. (Begründer des Labors für Künstliche Intelligenz am Massachusetts Institute of Technology)

Schritt 1: Die Diagonalsprache ist nicht semi-entscheidbar

Die Menge aller Turingmaschinen, die nicht halten, wenn sie ihre eigene Kodierung als Eingabe bekommen, wird als Diagonalsprache bezeichnet. Der Nachweis, dass die Diagonalsprache nicht semientscheidbar ist, geschieht durch einen Widerspruchsbeweis. Man nimmt an, dass eine Maschine existiert, welche die Diagonalsprache semi-entscheidet, und zeigt, dass dies zu einem logischen Widerspruch führt.

Angenommen, es gäbe eine Turingmaschine , die bei Eingabe der Beschreibung b(T) einer Turingmaschine den Wert ausgibt, wenn mit Eingabe b(T) nicht hält, und die nicht hält, wenn bei Eingabe von b(T) hält. Dann müsste bei Eingabe b(F) halten und ausgeben, wenn bei Eingabe b(F) nicht hält, und nicht halten, wenn bei Eingabe b(F) hält. Das ist ein Widerspruch, eine solche Maschine kann also nicht existieren.

Schritt 2: Das Komplement des Halteproblems ist nicht semi-entscheidbar

Wenn das Komplement des Halteproblems semi-entscheidbar wäre, dann wäre die Diagonalsprache ebenfalls semi-entscheidbar.

Angenommen, es gäbe eine Turingmaschine , die bei Eingabe der Beschreibung b(T) einer Turingmaschine und einer Zeichenkette 1 ausgibt, wenn mit Eingabe nicht hält, und die nicht hält, wenn bei Eingabe von hält. Man darf ohne Beschränkung der Allgemeinheit annehmen, dass die Eingabe für die Form b(T)*w hat. Dabei ist eine Zeichenkette, die weder in der Beschreibung b(T) der Turingmaschine noch in deren Eingabe vorkommt. Aus kann eine Turingmaschine konstruiert werden, die die Diagonalsprache semi-entscheidet. startet bei Eingabe einer Beschreibung b(T) einer Turingmaschine einfach mit der Eingabe b(T)*b(T) .

Wenn das Komplement des Halteproblems semi-entscheidet, so semi-entscheidet die Diagonalsprache. Da es eine solche Maschine nicht geben kann, die Konstruktion von aus aber sicher möglich ist, kann es eine solche Maschine nicht geben.

Schritt 3: Das Halteproblem ist nicht entscheidbar

Wenn das Halteproblem entscheidbar wäre, dann wäre sein Komplement semi-entscheidbar.

Angenommen, es gäbe eine Turingmaschine , die bei Eingabe der Beschreibung b(T) einer Turingmaschine und einer Zeichenkette 0 ausgibt, wenn mit Eingabe nicht hält, und die 1 ausgibt, wenn bei Eingabe von hält. Dann gäbe es auch eine Turingmaschine , die das Komplement des Halteproblems semi-entscheidet. startet bei Eingabe einer Beschreibung b(T) einer Turingmaschine einfach mit derselben Eingabe b(T)*w . Wenn 0 ausgibt, so gibt 1 aus. Wenn 1 ausgibt, so geht in eine Endlosschleife.

Wenn das Halteproblem entscheidet, so semi-entscheidet das Komplement des Halteproblems. Da es eine solche Maschine nicht geben kann, die Konstruktion von aus aber sicher möglich ist, kann es eine solche Maschine nicht geben.

Grafische Darstellung der Beweiskonstruktion

Maschine Eingabe	Maschine Eingabe	Maschine Eingabe
hält nicht	hält Ergebnisanzeige $0$	hält Ergebnisanzeige
hält	hält Ergebnisanzeige	hält nicht

Eine äquivalente Formulierung

Das Halteproblem mit leerem Eingabeband (englisch blank-tape halting problem, BTHP, auch als Null-Halteproblem bekannt) ist die Frage, ob eine Turingmaschine bei leerem Eingabeband anhält. Das BTHP ist genauso schwer wie das Halteproblem. Intuitiv ist das der Fall, weil eine Eingabe auch im Startzustand einer Turingmaschine kodiert werden kann.

Offensichtlich kann jede Maschine, die das Halteproblem für jede Turingmaschine mit jeder Eingabe entscheidet, auch das BTHP für entscheiden. Es kann aber auch eine Maschine , die für jede Turingmaschine das BTHP entscheidet, bereits das allgemeine Halteproblem entscheiden. Um das Halteproblem für die Turingmaschine mit Eingabe zu entscheiden, betrachtet die Turingmaschine $T_{w}$ , die wie folgt definiert ist. $T_{w}$ schreibt zuerst auf das Eingabeband, danach verhält sich $T_{w}$ wie . $T_{w}$ hält insbesondere genau dann auf dem leeren Band, wenn mit Eingabe hält.

Basierend auf einem Artikel in:

Wikipedia.de