Neutronenfluss

Name

Neutronenfluss

Volumenbezogenes Produkt aus Anzahl und Geschwindigkeit

$\Phi$

Größen- und Einheitensystem	Einheit	Dimension
SI	$\mathrm {\tfrac {1}{cm^{2}s}}$	$L^{-2}T^{-1}$

Brennelement-Viertel eines Druckwasserreaktors, projektive Darstellung: Das der Berechnung zugrunde gelegte Diskretisierungsgitter (unten), der thermische (Mitte) und der schnelle Neutronenfluss bei gezogenen Regelstäben. Zu sehen ist unter anderem, dass der Neutronenfluss ortsabhängig ist und innerhalb welcher Grenzen er variiert (s.u.).

Der Neutronenfluss (englisch Neutron flux), auch Neutronenflussdichte ist eine physikalische Größe der Kernphysik, und zwar eine skalare Größe. Anschaulich gibt er die Summe aller Wege an, die von den in einem Raumbereich vorhandenen freien Neutronen in einem Zeitintervall zurückgelegt werden, geteilt durch das Volumen des Raumbereichs und die Dauer des Zeitintervalls. Sein übliches Formelzeichen ist $\Phi$ (großes Phi), seine Dimension $\mathrm {L} ^{-2}\mathrm {T} ^{-1}$ . Die übliche Maßeinheit ist cm⁻² s⁻¹, der Deutlichkeit wegen meist geschrieben als n cm⁻² s⁻¹ („Neutronen pro Quadratzentimeter und Sekunde“).

Der Neutronenfluss ist weder ein Fluss noch eine Flussdichte im Sinne der sonst üblichen physikalischen Nomenklatur.

Er kann durch die Anzahldichte der Neutronen und den Mittelwert der Geschwindigkeitsbeträge der Neutronen ausgedrückt werden:

$\Phi =n\cdot v$ .

Der Neutronenfluss lässt sich mittels Neutronendetektoren messen.

Freie Neutronen treten in Sternen, in Supernovae und – verursacht durch kosmische Strahlung oder Gewitter – in unserer natürlichen irdischen Umgebung auf. Von besonderer Bedeutung sind der Neutronenfluss und einige mit ihm verwandte Größen in Kernreaktoren, Abschirmungen usw.

Definition

Der Neutronenfluss in einem Raumbereich ist definiert als:

$\Phi (t,{\vec {r}}):={\frac {1}{V}}\sum _{i}v_{i}$

Hier sind:

: die Zählvariable für die Neutronen (zu einer eventuellen Auswahl der gezählten Neutronen siehe "Neutronenwinkeldichte und weitere differentielle Größen")
: der Zeitpunkt, zu dem die Anzahl der Neutronen und deren Geschwindigkeit erfasst wird,
${\vec {r}}$ : der Ortsvektor, der die Lage des Raumbereichs angibt,
: das Volumen des betrachteten Raumbereichs,
$v_{i}$ : der Betrag der Geschwindigkeit ${\vec {v}}_{i}$ des -ten Neutrons.

Unabhängige Variable

Der Neutronenfluss hängt außer vom Ort auch von der kinetischen Energie der Neutronen ab und kann sich mit der Zeit ändern:

$\Phi =\Phi ({\vec {r}},E,t)$ .

Der Vektor ${\vec {r}}$ ist der Ortsvektor, der die Lage eines – im Grenzfall infinitesimal kleinen – Raumbereichs in einem dreidimensionalen Koordinatensystem angibt. Folglich hängt der Neutronenfluss im Allgemeinen von fünf unabhängigen Variablen ab.

Anschauliche Erklärung

Der Neutronenfluss im Raumpunkt ${\vec {r}}$ lässt sich auch veranschaulichen durch die Vorstellung einer kleinen Kreisscheibe mit dem Mittelpunkt ${\vec {r}}$ , die von den Neutronen durchdrungen wird. Man stellt sich vor, die Kreisscheibe werde bei festem Mittelpunkt für jedes einzelne Neutron so im Raum gedreht, dass das Neutron in Richtung der Normalen einfällt. Der Neutronenfluss ist dann die Zahl der Neutronen, die in einem Zeitintervall die Scheibe durchdringen, geteilt durch das Zeitintervall und durch die Fläche der Scheibe. Das Drehen der Scheibe in alle Richtungen ergibt als Einhüllende eine Kugel mit dem Durchmesser der Scheibe.

Neutronenwinkeldichte und weitere differentielle Größen

Die Auswahl der zum Zeitpunkt zu zählenden Neutronen im Volumen um den Ort ${\vec {r}}$ kann danach erfolgen, ob die Neutronen eine Energie $E_{i}$ innerhalb eines Energiebereichs $E-\delta E\leq E_{i}\leq E+\delta E$ haben und zugleich ihre Flugrichtung $\hat e_i$ in der Umgebung einer vorgegebenen Flugrichtung mit dem Einheitsvektor $\vec\Omega$ liegt ( ${\hat {e}}_{i}\cdot {\vec {\Omega }}\geq 1-\delta e$ ). Daraus ergibt sich die differentielle Größe Neutronenwinkeldichte (englisch angular neutron density) oder kurz Winkeldichte :

$n({\vec {r}},E,t,{\vec {\Omega }}):=\lim _{V\rightarrow 0}\lim _{\delta E\rightarrow 0}\lim _{\delta e\rightarrow 0}{\frac {1}{V}}{\frac {1}{\delta E}}{\frac {1}{4\pi (\delta e)^{2}}}\Phi (t,{\vec {r}},V,E,\delta E,{\vec {\Omega }},\delta e)$ .

Eine genaue Analyse der Transportprozesse von Neutronen in einem Kernreaktor (entsprechend auch von anderen Teilchen) erfordert die Definition noch weiterer, mit dem Neutronenfluss verknüpfter Größen. Die Namen dieser Größen sind nicht in allen reaktorphysikalischen Lehrbüchern gleich. Wir folgen hier der Namensgebung und der Definition einiger dieser Größen nach dem Lehrbuch Nuclear reactor theory von Bell und Glasstone.

Neutronenflussspektrum

Die Größe Neutronenflussspektrum, Neutronenspektrum, Neutronenenergiespektrum, energiediffenzieller Neutronenfluss oder energieabhängiger Neutronenfluss ist die partielle Ableitung des Neutronenflusses nach der Energie:

$\varphi ({\vec {r}},E,t)={\frac {\partial \Phi ({\vec {r}},E,t)}{\partial E}}$ .

Die Maßeinheit ist dementsprechend z.B. n cm⁻²s⁻¹eV⁻¹, Neutronen pro Quadratzentimer, Sekunde und Elektronenvolt. Der Fluss der Neutronen mit Energien zwischen und $E+\partial E$ ist $\varphi (E)\,\partial E$ .

Flugrichtung der Neutronen

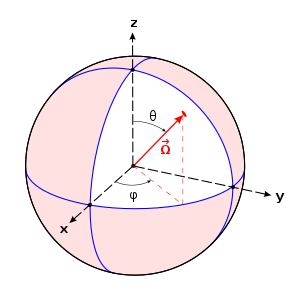
Der Einheitsvektor der Neutronenflugrichtung $\vec{\Omega}$ und seine Komponenten, der Polarwinkel $\theta$ und der Azimutwinkel $\varphi$ in Kugelkoordinaten

Um Neutronen nach ihrer Flugrichtung zu unterscheiden, sind zwei weitere unabhängige Variable erforderlich, die in dem Vektor Neutronenflugrichtung (Einheitsvektor der Neutronenflugrichtung) zusammengefasst werden.

Folgendes sei vorangestellt: Es gibt Größen in der Physik, die vom Ort und vom Impuls abhängen, zum Beispiel die Wellenfunktion der Quantenmechanik. Für solche Größen werden neben den Ortskoordinaten ${\vec {r}}=(x,y,z)$ auch die Impulskomponenten $\vec p = (p_x,p_y,p_z)$ als unabhängige Variable in die Symbolik aufgenommen. Sei so eine Größe, die außerdem von der Zeit abhängt, dann symbolisiert man die Abhängigkeit der Größe von sieben unabhängigen Variablen mit $f({\vec {r}},{\vec {p}},t)$ .

In der Reaktorphysik könnte man ebenfalls mit diesen sieben unabhängigen Variablen rechnen, den drei Ortskoordinaten, den drei Impulskomponenten und der Zeit. Aber anstelle der drei Impulskomponenten wählt man drei andere unabhängige Variable, die kinetische Energie der Neutronen und zwei Raumwinkelvariable ${\vec {\Omega }}=(\theta ,\varphi )$ , die die Flugrichtung der Neutronen erfassen. Es sind der Polarwinkel $\theta$ und der Azimutwinkel $\varphi$ der (auf den Wert 1 normierten) Flugrichtung in Kugelkoordinaten, wie in der Abbildung gezeigt.

Der Vektor $\vec{\Omega}$ , der Einheitsvektor in Richtung der Neutronenbewegung, wird definiert durch

${\vec {\Omega }}={\frac {{\vec {v}}(E)}{|{\vec {v}}(E)|}}={\frac {{\vec {v}}(E)}{v(E)}}$ .

Dabei symbolisieren ${\vec {v}}(E)$ den Geschwindigkeitsvektor, $|{\vec {v}}(E)|$ und v(E) den Betrag des Geschwindigkeitsvektors, jeweils in Abhängigkeit von der kinetischen Energie .

Man beachte den Unterschied zwischen diesem zweikomponentigen Vektor $\vec{\Omega}$ und dem gewöhnlichen Raumwinkel, der ein Skalar ist und mit $\Omega$ symbolisiert wird, was zu Fehlinterpretationen führen kann.

Mit diesen unabhängigen Variablen symbolisiert man eine reaktorphysikalische Größe dann entsprechend mit $f({\vec {r}},E,{\vec {\Omega }},t)$ . Diese Wahl der unabhängigen Variablen hat sich als zweckmäßig erwiesen und ist aus physikalischer Sicht einer Wahl der Impulskomponenten gleichwertig. Aus der kinetischen Energie und dem Raumwinkelvektor können die Impulskomponenten berechnet werden und umgekehrt.

Neutronenwinkelfluss

Der Neutronenwinkelfluss (Angular neutron flux) oder kurz Winkelfluss ist die abhängige Variable der Neutronentransportgleichung (Neutron transport equation) und damit eine der wichtigsten physikalischen Größen der Reaktortheorie überhaupt. Sie wird definiert als

$\psi ({\vec {r}},E,{\vec {\Omega }},t)=v\cdot n({\vec {r}},E,{\vec {\Omega }},t)$ .

Neutronenfluss oder Neutronenskalarfluss

Aus dem Neutronenwinkelfluss ergibt sich der oben definierte Neutronenfluss einfach als Integral des Winkelflusses über alle Raumrichtungen:

$\Phi ({\vec {r}},E,t)=\int _{4\pi }d{\vec {\Omega }}\psi ({\vec {r}},E,{\vec {\Omega }},t)$ .

Weil der Neutronenfluss durch Integration über die vektorielle Größe Neutronenwinkelfluss gebildet wird, bezeichnet man den Neutronenfluss im Kontext der Neutronentransporttheorie auch als Neutronenskalarfluss oder skalaren Neutronenfluss.

Neutronenfluenz

Durch Integration des Neutronenflusses oder des Neutronenflussspektrums über die Zeit, z.B. die Dauer einer Bestrahlung, ergibt sich entsprechend die totale bzw. energieabhängige Neutronenfluenz. Sie ist wichtig zur Berechnung z.B. der durch Neutronen verursachten Strahlenschäden oder der Ausbeute einer Neutronenaktivierung.

Bedeutung für Kernreaktoren

Die Größe Neutronenfluss dient im Zusammenhang mit Kernreaktoren hauptsächlich dazu, die Frage zu beantworten, ob und warum eine Spaltstoffanordnung (Kernreaktor) kritisch wird, und um Kernreaktionsraten im Reaktor zu berechnen. Ohne Kenntnis räumlich und energetisch hinreichend „aufgelöster“ Kernreaktionsraten können beide Fragen nicht beantwortet werden. Die entscheidende Größe Kernreaktionsratendichte ist das Produkt aus Neutronenfluss und der materialabhängigen Größe makroskopischer Wirkungsquerschnitt. Der makroskopische Wirkungsquerschnitt hängt von Teilchendichten und nuklearen Eigenschaften aller Nuklide ab, mit denen sich die Neutronen den Raumbereich „teilen“.

In einem Kernreaktor ist der Neutronenfluss im Allgemeinen abhängig von Ort, Neutronenenergie und Zeit. In einem gleichbleibend kritisch gehaltenen Reaktor kann man die Zeitabhängigkeit über eine kleine Zeitspanne vernachlässigen. Man spricht dann vom stationären Zustand des Reaktors. Der totale oder der thermische Neutronenfluss ist relativ einfach zu messen, z.B. mit in den Reaktorkern eingebauten Spaltkammern.

Aus dem Produkt von Neutronenfluss und einem speziellen Wirkungsquerschnitt, einer material- und ortsabhängigen Größe, ergibt sich die Leistungsdichte in einem Volumenbereich des Reaktors. Nimmt man (etwas vereinfachend) an, dass die Form der räumlichen Verteilung des Neutronenflusses über den Reaktorkern immer gleich bleibt, dann genügt die Messung des Neutronenflusses an einer Stelle, um auf die Gesamtleistung des Reaktors zu schließen. Eine Temperaturmessung wäre dagegen als Leistungsmaß nicht geeignet, denn die Temperatur an einer Stelle ist Resultat der Leistung an der Stelle selbst, der Leistung in benachbarten Bereichen in der jüngeren und mittleren Vergangenheit sowie der Kühlleistung.

Das Fluss-Messsignal wird daher allgemein zur Steuerung und Überwachung des Reaktors verwendet. Auch bei abgeschaltetem (unterkritischem) Reaktor wird die Flussmessung ständig in Betrieb gehalten. Eine zu diesem Zweck eingebaute radioaktive Neutronenquelle sorgt stets für einen geringen Neutronenfluss; dadurch wird die Funktion der Messinstrumentierung dauernd überwacht.

Mittelwert und Diskretisierung

Ein gemessener Neutronenflusswert ist stets ein Mittelwert über einen gewissen Raumbereich, ein Energieintervall und eine Zeitdauer. Auch für Berechnungen des Neutronenflusses ist eine Diskretisierung der unabhängigen Variablen notwendig, da die entsprechenden Gleichungen nur numerisch lösbar sind. Die Intervallgrößen für die Diskretisierung werden in der Regel vor dieser Berechnung festgelegt.

Räumliche Diskretisierung

Größe und Form des interessierenden Raumbereichs können sehr unterschiedlich sein. Bei einer ausgedehnten Anordnung, etwa einem Reaktorkern, setzt die verfügbare Rechenkapazität der Auflösung in kleine Raumbereiche praktische Grenzen. Wie fein die Ortsauflösung gewählt werden muss, hängt zusammen mit der mittleren freien Weglänge der Neutronen; diese wird durch die Neutronenenergie und das jeweilige Medium bestimmt. Typische Abmessungen der einzelnen „Zelle“ bei Reaktorberechnungen liegen im Zentimeterbereich.

Energiediskretisierung

Neutronenflussspektrum des Brennelements eines Druckwasserreaktors in doppelt logarithmischer Darstellung. Das der Berechnung zugrunde gelegte Diskretisierungsgitter ist rechts oben als Miniaturbild dargestellt.

Die Energieauflösung wird in Reaktorberechnungen je nach Fragestellung gewählt, vom Gesamtbereich der möglichen Neutronenenergie (10⁻⁴ bis 2·10⁷) eV – also gar keiner „Auflösung“ – bis hin zu einigen hundert Energieintervallen („Neutronengruppen“). Bei thermischen Reaktoren reicht für manche Fragestellungen die Unterteilung in zwei Gruppen aus (thermischer Fluss und schneller Fluss; siehe erste Abbildung). Für schnelle Reaktoren sind Berechnungen z.B. oft mit 26 Gruppen durchgeführt worden.

Durch Integration des Neutronenflussspektrums über das Energieintervall der jeweiligen Neutronengruppe werden die sogenannten Gruppenflüsse berechnet. Dies sind zum Beispiel im Fall von zwei Energiegruppen die Integrale

$\Phi _{\text{thermisch}}=\int _{E_{u}}^{E_{1}}\varphi ({\vec {r}},E,t)\ \mathrm {d} E$ (thermischer Fluss) und

$\Phi _{\text{schnell}}=\int _{E_{1}}^{E_{o}}\varphi ({\vec {r}},E,t)\ \mathrm {d} E$ (schneller Fluss).

Im Beispiel der ersten Abbildung wurden die Energiegrenzen $E_{u}=10^{-4}\ \mathrm {eV}$ , $E_{1}=0{,}625\ \mathrm {eV}$ und $E_{o}=20\ \mathrm {MeV}$ verwendet.

Das Neutronenflussspektrum wird u.a. als Wichtungsfunktion benötigt, um die sog. Gruppenkonstanten für Neutronendiffusionsberechnungen zu erhalten.

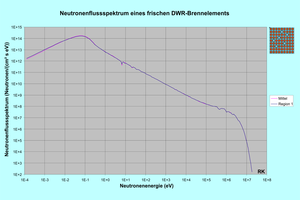
Die Abbildung zeigt das Neutronenflussspektrum eines frischen Brennelements eines Druckwasserreaktors (DWR). Es handelt sich um das gleiche Modell, zu dem auch die am Artikelanfang abgebildeten Neutronenflussverteilungen gehören, und wurde ebenfalls mit dem Programmsystem HELIOS 1.8 berechnet. Dargestellt ist das Neutronenflussspektrum einer ausgewählten Kühlmittelregion (Region 1, die Region an der linken oberen Ecke) und der Mittelwert des Neutronenflussspektrums, gemittelt über das gesamte Brennelement. Man erkennt:

Die Energie beim Maximum des Neutronenflussspektrums liegt nahe an der thermischen Energie von 0,0253 eV (20 °C).
Das Neutronenflussspektrum bricht bei etwa 20 MeV ab, da durch Kernspaltung keine Neutronen mit einer höheren Energie entstehen.

Beispiel: Neutronenfluss in einem Druckwasserreaktor

Querschnitte durch Berechnungszellen des betrachteten Druckwasserreaktors: Zelle mit Brennstab und Zelle mit Regelstab-Führungsrohr. Jeweils links Schema der Zelle, rechts die diskretisierte Zelle

Querschnitt durch ein Viertel eines Brennelements des betrachteten Druckwasserreaktors

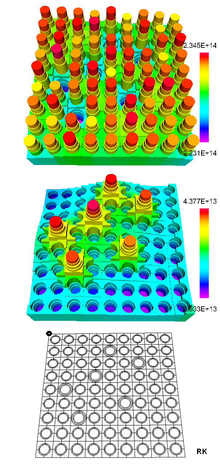
Die erste Abbildung des Artikels zeigt die horizontale Ortsabhängigkeit des thermischen und des schnellen Neutronenflusses über den Querschnitt eines Brennelements eines Druckwasserreaktors in einem stationären Zustand, gewonnen aus einer Neutronentransportrechnung mit dem Zell- und Abbrandprogramm HELIOS 1.8 und Wirkungsquerschnitten aus der Kerndatenbibliothek ENDF/B-VI data files (Rose and Dunford, 1990).

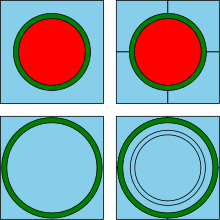
Das Gitter des Brennelements enthält zwei Typen von „Zellen“: Brennstabzellen und Führungsrohrzellen. Die Brennstabzelle enthält drei Materialien: Brennstoff (rot), Zirkalloy-Hülle (grün) und Wasser (blau), die Führungsrohrzelle nur das Führungsrohr und Wasser. Die nebenstehende Abbildung zeigt links die beiden Zelltypen und rechts daneben ihre Diskretisierung in 6 bzw. 8 Regionen.

Das Brennelement ist eine 18×18-Anordnung mit 300 Brennstäben und 24 Regelstabführungsrohren, in die Neutronenabsorber eintauchen können. In dieser Rechnung sind die Regelstäbe gezogen. Da das Brennelement symmetrisch ist, reichte es aus, ein Viertel des Brennelements zu berechnen, das die Grafik zeigt. Das Symmetriezentrum (die Mitte des Brennelement-Querschnitts) ist auf dem Diskretisierungsgitter links oben als kleines schwarzes Quadrat markiert.

An den Orten der gezogenen Regelstäbe ist der thermische Fluss stark erhöht, im mittleren Teil der ersten Abbildung des Artikels deutlich an den sechs rot bis orange eingefärbten Maxima zu erkennen. Der schnelle Fluss dagegen ist an diesen Orten vergleichsweise niedrig. Die Zahlen innerhalb der Abbildung geben die Flusswerte in n cm⁻²s⁻¹ bei einer spezifischen Wärmeleistung von 37,4 W/g Schwermetall an. In diesem Modellfall liegt der schnelle Fluss im Intervall (2,2·10¹⁴ – 2,3·10¹⁴) Neutronen cm⁻²s⁻¹, der thermische Fluss im Intervall (2,9·10¹³ – 4,4·10¹³) Neutronen cm⁻²s⁻¹.

Kernreaktoren

Die Neutronenflusswerte (genauer: Neutronenwinkelflusswerte) in einem Kernreaktor gehorchen der Neutronentransportgleichung, einer Bilanzgleichung für Neutronen. Diese Integro-Differentialgleichung numerisch zu lösen gehört zu den anspruchsvollsten Aufgaben der Physik und numerischen Mathematik überhaupt.

Programmsysteme zur numerischen Lösung der Neutronentransportgleichung, zum Beispiel für ein Kernreaktor-Brennelement in einer räumlichen und energetischen Auflösung, wie sie in der Abbildung am Anfang des Artikels dargestellt ist, werden von nur sehr wenigen spezialisierten Firmen auf der Welt entwickelt. Es sind entweder staatlich dominierte Firmen, zum Beispiel in Frankreich unter dem Dach der Électricité de France (EDF) oder dem Commissariat à l’énergie atomique et aux énergies alternatives (CEA) (Programmsystem APOLLO), oder privatrechtliche Firmen wie Studsvik Scandpower (Programmsysteme CASMO und HELIOS). Die privatrechtlichen Firmen sind meist durch Outsourcing von Arbeitsgruppen entstanden, die mit der Programmentwicklung in einem staatlichen Institut oder an einer Universität begonnen haben. Die Entwicklung solcher Programmsysteme erfordert Dutzende von Personenjahren und kann an einer Universität gegenwärtig nicht geleistet werden. Hinzu kommt für jeden Entwickler eine Einarbeitungszeit in die physikalische Theorie und die mathematisch-numerischen Lösungsverfahren von mehreren Jahren, ehe er mit dem Programmieren überhaupt beginnen kann. Auch ein Anwender eines solchen Programms sollte für die Einarbeitung etwa drei bis fünf Jahre veranschlagen.

Für die Entwicklung neuer Kernreaktortypen, zum Beispiel eines Salzschmelzenreaktors für den Leistungsbetrieb oder für den Routinebetrieb eines existierenden Kernkraftwerks, ist eine ganze Kette von Programmen erforderlich, u.a. auch weit weniger „aufwendige“ Neutronentransportprogramme, die Spezialaufgaben numerisch lösen. Das erste Glied dieser Kette bleibt aber stets ein hochleistungsfähiges Neutronentransportprogramm. Der gängige Typname Zell- und Abbrandprogramm für ein solches Programm umschreibt dessen Leistungsumfang nur andeutungsweise. Diese Zell- und Abbrandprogramme wurden (Stand Jahr 2007) ausschließlich in Fortran unterschiedlicher Versionen geschrieben. Ein Programmsystem dieses Typs kostete im Jahr 2000 mindestens 100000 Dollar.

Das Verhalten der Neutronen im Reaktor kann jedoch angenähert auch als Diffusionsvorgang beschrieben werden. Ein solches Neutronendiffusionsprogramm berechnet ausschließlich den Neutronenfluss, nicht den Neutronenwinkelfluss. Ein Programm dieses Typs kann, grob überschlagen, in zwei bis fünf Personenjahren (je nach räumlicher Dimension: 1D, 2D, 3D) entwickelt werden. Die übliche Programmiersprache für ein Neutronendiffusionsprogramm ist ebenfalls Fortran. Programme dieses Typs werden für öffentliche Institute und Universitäten kostenlos von der Datenbank der NEA Computer Program Library, speziell unter der Kategorie C. STATIC DESIGN STUDIES bereitgestellt (Einarbeitungszeit einige Monate).

Für spezielle Aufgaben werden auch Monte-Carlo-Rechenprogramme wie MCNP („Monte-Carlo N-Particle Transport Code“) eingesetzt.

Fusionsreaktoren

Zur Berechnung der Neutronenflussverteilung und damit zusammenhängender Größen in Fusionsreaktoren und entsprechenden Versuchsanlagen wird allgemein die Monte-Carlo-Methode eingesetzt.

Natürlicher Neutronenfluss

Neutroneninduzierte Kernreaktionen in AGB-Sternen (englisch Asymptotic giant branch) sind für die meisten natürlichen Elemente verantwortlich, die durch Nukleosynthese entstanden sind. Das sind Elemente massereicher als Eisen. Der Neutronenfluss ist relativ niedrig und liegt in der Größenordnung von 10⁵ bis 10¹¹ n cm⁻²s⁻¹. Er führt zur Nukleosynthese durch den s-Prozess (englisch Slow-Neutron-Capture-Prozess).

Im Gegensatz dazu ist der Neutronenfluss nach der Explosion eines massereichen Sterns (Supernova) sehr hoch und erreicht die Größenordnung von 10²² n cm⁻²s⁻¹. Das führt zur Nukleosynthese durch den r-Prozess (englisch Rapid-Neutron-Capture-Prozess).

In der Erdatmosphäre erzeugt die kosmische Strahlung, die vorwiegend aus hochenergetischen Protonen (1 GeV und höher) besteht, durch Spallation der Atomkerne von Stickstoff und Sauerstoff freie Neutronen. Zugleich erzeugt sie sekundäre Protonen und geladene und neutrale Pionen, die ihrerseits in weiteren Reaktionen Neutronen freisetzen können. Der so entstehende Neutronenfluss hängt stark vom primären Protonenstrom und dem Ort der Reaktion in der Atmosphäre ab.

Bei einem Blitz werden Atome des atmosphärischen Stickstoffs und Sauerstoffs ionisiert, aber auch das in einer Wasserdampfwolke immer vorhandene schwere Wasser. Im elektrischen Feld der Blitzentladung können die Ionen (wie die freigesetzten Elektronen auch) beschleunigt werden und Kernreaktionen auslösen, die ihrerseits Neutronen freisetzen. Insbesondere kann es auch zu Fusionsreaktionen kommen. Für diese Vorgänge stehen Theorie und Experiment noch am Anfang. Der atmosphärische Neutronenfluss während eines Gewitters erreicht bis zu etwa 90 n cm⁻²s⁻¹.

Weitere Zahlenbeispiele für den Neutronenfluss

Vom „Komitee Forschung mit Neutronen“ werden Forschungsneutronenquellen (FNQ) unterschieden in

Spallationsquellen. Es gibt 2 Spallations-Neutronenquellen in Europa.
Reaktoren mit hohem Neutronenfluss ( $\Phi _{{\mathrm {th}}}$ > 10¹⁵ n cm⁻²s⁻¹). Es gibt einen solchen Hochflussreaktor in Europa, und zwar im Institut Laue-Langevin (ILL).
Reaktoren mit mittlerem Neutronenfluss (10¹⁴ n cm⁻²s⁻¹ < $\Phi _{{\mathrm {th}}}$ < 10¹⁵ n cm⁻²s⁻¹). Es gibt 3 solche FNQ in Europa.
Reaktoren mit niedrigem Neutronenfluss ( $\Phi _{{\mathrm {th}}}$ ≤ 10¹⁴ n cm⁻²s⁻¹). Es gibt 7 solche FNQ in Europa.

$\Phi _{{\mathrm {th}}}$ meint den thermischen Neutronenfluss.

Die Spallations-Neutronenquelle Paul Scherrer Institut/ETH Zürich erreicht einen totalen Neutronenfluss von 10¹⁴ n cm⁻²s⁻¹, der Forschungsreaktor FRM-II 8×10¹⁴ n cm⁻²s⁻¹.

In einem Fusionsreaktor wird die Wand des Plasmagefäßes ebenfalls einem Neutronenfluss von etwa 10¹⁴ n cm⁻²s⁻¹ ausgesetzt sein, der hier ganz überwiegend aus Neutronen der hohen Energie von etwa 14 MeV besteht.

Basierend auf einem Artikel in:

Wikipedia.de