Spektrale Leistungsdichte

Leistungsdichtespektrum eines Signals

Die spektrale Leistungsdichte gibt die auf die Frequenz bezogene Leistung eines Signals in einem infinitesimalen Frequenzband an. Diese Dichte besitzt die Dimension Leistung · Zeit, die Angabe erfolgt meist in den Einheiten Watt/Hertz oder dBm/Hz. Wird die spektrale Leistungsdichte über dem Frequenzspektrum angegeben, entsteht ein Leistungsdichtespektrum (LDS) oder Autoleistungsspektrum (engl.: Power-Spectral-Density (PSD), auch Wirkleistungsspektrum). Das Integral über alle Frequenzen ergibt die Gesamtleistung eines Signals. Während die Fouriertransformation von stationären Prozessen (wie z.B. Rauschen oder monofrequente Signale) unbeschränkt ist, lassen sich derartige Signale mit Hilfe der LDS quantitativ analysieren. Das LDS ist die Anzeigeform von Spektralanalysatoren, wobei hier die Leistung über vorgegebenen Frequenzintervallen (engl.: resolution bandwidth (RBW)) angegeben wird.

Allgemeines und Definition

Da für stationäre Prozesse f(t) im Allgemeinen weder die Energie $\|f\|_{2}^{2}$ noch die Fouriertransformierte $F{\big (}f{\big )}(\omega )$ im klassischen Sinn existieren, liegt es nahe, zeitlich begrenzte Anteile $f_{T}(t)=f(t)$ für $|t|\leq T$ und $0$ sonst zu betrachten. Nach der Formel von Plancherel gilt

${\frac {1}{2T}}\int \limits _{{\mathbb{R} }}|f_{T}(t)|^{2}{\mathrm {d}}t={\frac {1}{2T}}\int \limits _{{\mathbb{R} }}|F(f_{T})(\omega )|^{2}{\mathrm {d}}\omega$

Falls die mittlere Signalleistung

$r_{{XX}}(0):=\lim \limits _{{T\to \infty }}{\frac {1}{2T}}\int \limits _{{-T}}^{T}|f(t)|^{2}{\mathrm {d}}t$

existiert, existiert auch die rechte Seite obiger Formel und als spektrale Beschreibung der Leistung kann man die Spektrale Leistungsdichte definieren (falls der Grenzwert existiert) als

$S_{{XX}}(\omega ):=\lim \limits _{{T\to \infty }}{\frac {1}{2T}}|F(f_{T})(\omega )|^{2}$

Für jedes endliche heißt die Größe ${\text{Per}}_{T}(\omega ):={\frac {1}{2T}}|F(f_{T})(\omega )|^{2}$ das Periodogramm von . Es stellt einen Schätzwert der Spektralen Leistungsdichte dar, dessen Erwartungswert aber nicht $S_{{XX}}(\omega )$ entspricht (nicht erwartungstreu) und dessen Varianz auch für beliebig große nicht verschwindet (nicht konsistent).

Eigenschaften und Berechnung

Zur Bestimmung der spektralen Leistungsdichte $S_{{XX}}(\omega )$ wird oft das Wiener-Chintschin-Theorem herangezogen, wo sie über die Fouriertransformation der zeitlichen Autokorrelationsfunktion $r_{{xx}}(t)$ des Signals gegeben wird:

$S_{XX}(\omega) = F(r_{xx})(\omega) = \frac{1}{2\pi} \int_{-\infty}^{\infty} r_{xx}(t) e^{-i\omega t} \mathrm{d}t$

Dabei ist

$r_{{xx}}(t)=\lim _{{T\to \infty }}{\frac {1}{2T}}\int _{{-T}}^{{T}}f(\tau )\;\overline {f(t+\tau )}{\mathrm {d}}\tau$

die Autokorrelationsfunktion des zeitlichen Signals f(t) . Für Rauschsignale, allgemein für Prozesse, muss die Ergodizität vorausgesetzt werden, die es erlaubt Eigenschaften der Zufallsvariablen, wie den Erwartungswert, aus einer Musterfunktion zu bestimmen. In der Praxis kann nur ein endliches Zeitfenster betrachtet werden, weshalb man die Integrationsgrenzen einschränken muss. Nur für eine stationäre Verteilung ist die Korrelationsfunktion nicht mehr von der Zeit abhängig.

Das Autoleistungsdichtespektrum ist gerade, reell und positiv. Dies bedeutet einen Informationsverlust, der eine Umkehrung dieser Prozedur verhindert.

Wird ein (Rausch-)Prozess mit Leistungsdichtespektrum $S_{{XX}}(\omega )$ über ein lineares, zeitinvariantes System mit Übertragungsfunktion $H(\omega )$ übertragen, so ergibt sich am Ausgang ein Leistungsdichtespektrum von

$S_{{YY}}(\omega )=|H(\omega )|^{2}\cdot S_{{XX}}(\omega ).$

Die Übertragungsfunktion geht quadratisch in die Formel ein, da das Spektrum eine Leistungsgröße ist.

Das Autoleistungsspektrum kann als einseitiges Spektrum $G_{XX}(f)(f\geq 0)$ dargestellt werden. Es gilt dann:

$G_{{XX}}=S_{{XX}}(f)\quad {\mathrm {f{\ddot u}r}}\quad f=0$

und

$G_{{XX}}=2S_{{XX}}(f)\quad {\mathrm {f{\ddot u}r}}\quad f>0\,.$

Berechnungsmethoden beschränken sich üblicherweise auf bandbeschränkte Signale (Signale deren LDS für große Frequenzen verschwindet), die eine diskrete Darstellung erlauben (Nyquist-Shannon-Abtasttheorem). Erwartungstreue, konsistente Schätzwerte bandbegrenzter Signale, die auf einer Modifizierung des Periodogramms beruhen, sind beispielsweise die Welch-Methode oder Bartlett-Methode. Schätzungen auf Basis der Autokorrelationsfunktion heißen Korrelogramm-Verfahren wie beispielsweise die Blackmann-Tukey-Schätzung.

Anwendung und Einheiten

Die Kenntnis und Analyse der spektralen Leistungsdichte von Nutzsignal und Rauschen ist wesentlich zur Bestimmung des Signal-Rausch-Verhältnisses und zur Optimierung entsprechender Filter zur Rauschunterdrückung, zum Beispiel im Bildrauschen.

Das Autoleistungsspektrum kann für Aussagen über den Frequenzgehalt der analysierten Signale herangezogen werden. Spektralanalysatoren untersuchen die Spannung von Signalen. Für die Anzeige in Leistung ist die Angabe des Abschlusswiderstandes erforderlich. Mittels Spektralanalysatoren lässt sich aber die Spektralleistung nicht in einem infinitesimalen Frequenzband, sondern nur in einem Frequenzintervall endlicher Länge, bestimmen. Die so erhaltene spektrale Darstellung heißt Mean-Square-Spektrum (MSS) und ihre Wurzel RMS-Spektrum (engl. Root-Mean-Square). Die Länge des Frequenzintervalls ist stets mit angegeben und heißt Auflösebandbreite (engl. Resolution Bandwidth, kurz RBW oder BW) in der Einheit [Hz]. Die Umrechnung in Dezibel ist, wie für Leistungsangaben standardisiert, gemäß ${\text{MSS}}_{{dB}}=10\log _{{10}}({\text{MSS}})$ , während die Umrechnung für RMS gemäß ${\text{RMS}}_{{dB}}=20\log _{{10}}({\text{RMS}})$ erfolgt, womit die beiden Anzeigen in Dezibel zahlenmäßig identisch sind. Als Einheiten werden u.a. [dBm], [dBV], RMS-[V], PK-[V] (von engl. peak) verwendet. Die Angaben beziehen sich stets auf die verwendete Auflösebandbreite [Hz]. Beispielsweise erzeugt ein Sinussignal mit einem Spannungsverlauf von $f(t)=10\sin(\omega t)$ V an einem Abschlusswiderstand von 50 Ohm eine effektive Spannung von 30 dBm oder 16,9897 dBV oder 7,0711 V (RMS) oder 10 V (PK) für jede Auflösebandbreite.

Beispiele

LDS eines monofrequenten Signals mit Quantisierungsrauschen

Wenn die Korrelationsfunktion eine Delta-Distribution ist, spricht man von weißem Rauschen, in diesem Fall ist $S_{{XX}}(\omega )$ konstant.
Für das thermische Rauschen, genauer die spektrale Rauschleistungsdichte, gilt: N₀ =k_B·T. Bei 27 °C beträgt es 4·10⁻²¹ J = 4·10⁻²¹ W/Hz = -204 dBW/Hz = -174 dBm/Hz
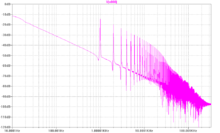
Im Bild rechts ist ein MSS von der Funktion $f(t)=\sin(2\pi 3500t)+2^{{-16}}R(t)$ mit einem gleichverteilten Rauschprozess (Quantisierungsrauschen) $|R(t)|\leq 1$ bei einer Abtastrate von 44100 Hz und einer Auflösebandbreite von BW = 43,1 Hz (resultierend aus 44100 Hz / 1024 FFT Punkte) zu sehen, wie es beispielsweise von einer CD kommen könnte. Die Spitze bei etwa −3 dB repräsentiert das Sinussignal auf dem Rauschgrund bei etwa −128 dB. Da die Leistungsangaben sich auf die Auflösebandbreite beziehen, kann man das SNR zu $-3-(-128+10\log _{{10}}(22050/{\text{BW}}))=97{,}9\,{\mathrm {dB}}$ ablesen (beachte das Logarithmusgesetz, das Multiplikationen in Additionen transformiert). Das aus dem Bild abgelesene SNR kommt damit dem theoretisch erwarteten von $10\log _{{10}}(1^{2}/2)-10\log _{{10}}((2^{{-16}})^{2}/3)=98{,}0905\,{\mathrm {dB}}$ recht nahe.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de