Lichtstärke (Photometrie)

Name

Lichtstärke

$I_{{\mathrm {v}}}$

Größen- und Einheitensystem	Einheit	Dimension
SI	Candela (cd)	J

Die Lichtstärke (englisch: luminous intensity, Formelzeichen I_v) gibt den auf den Raumwinkel bezogenen Lichtstrom an. Sie ist eine Basisgröße im SI-Einheitensystem. Ihre SI-Einheit ist die Candela (cd).

Der Index v (für visuell) kennzeichnet die Lichtstärke als photometrische Größe, die über den radiometrischen Aspekt hinaus den physiologischen Einfluss der Hellempfindlichkeitskurve einbezieht.

Die Definition der Lichtstärke mit Bezug auf den Raumwinkel setzt ein Lichtbündel voraus, das bezügliche eines Punkts divergiert oder konvergiert. Die korrespondierende Größe mit Bezug auf eine beschienene bzw. durchströmte Fläche ist die Beleuchtungsstärke oder Lichtstromdichte.

Beispiel 1: Kugelstrahler

Ein Kugelstrahler ist eine ideale Lichtquelle, die ihr Licht gleichmäßig in alle Richtungen des Raums abgibt. (Eine frei im Raum hängende Glühlampe ohne Lampengehäuse bildet eine gute Näherung.) Wenn dieser Kugelstrahler sich im Zentrum einer fiktiven Kugel mit dem Radius r = 1 m befindet und einen Lichtstrom von 1256 Lumen abgibt, trifft auf jeden Quadratmeter der fiktiven Kugeloberfläche der Lichtstrom(anteil) von 100 Lumen. Dem Kugelstrahler kann somit für jede beliebige Richtung im Raum die Lichtstärke I_v = 100 cd zugeordnet werden. Die Formeln für dieses Beispiel:

$I_{\mathrm {v} }\,=\,{\frac {\Phi _{\mathrm {v} }}{\Omega }}\,;\qquad I_{\mathrm {v} }\,=\,{\frac {1256\,lm}{4\,\pi \,sr}}\,;\qquad I_{\mathrm {v} }\,=\,100\,cd$

Beispiel 2: Scheinwerfer mit 1sr Ausleuchtung

Scheinwerfer

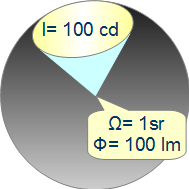
Bei einer fiktiven Lichtquelle, die ihr gesamtes Licht in einen Raumwinkel der Größe Ω = 1 sr abgibt wird der Raum innerhalb des Raumwinkels Ω gleichmäßig durchstrahlt, der Raum außerhalb des hellen Raumwinkels bleibt völlig dunkel. (Ein Scheinwerfer könnte eine gute erste Näherung bilden.) Gibt ein solcher Strahler mit Φ_v = 100 lm seinen gesamten Lichtstrom in den beleuchteten Raumwinkel Ω = 1 sr ab, beträgt die Lichtstärke innerhalb des hellen Raumwinkels definitionsgemäß I_v = 100 cd. Außerhalb des beleuchteten Raumwinkels beträgt die Lichtstärke I_v = 0 cd. Bei diesem Strahler sind Lichtstrom und Lichtstärke bis auf die Bezeichnung für die jeweilige Maßeinheit gleich. Die Formeln für dieses Beispiel:

$I_{\mathrm {v} }\,=\,{\frac {\Phi _{\mathrm {v} }}{\Omega }}\,;\qquad I_{\mathrm {v} }\,=\,{\frac {100\,lm}{1\,sr}}\,;\qquad I_{\mathrm {v} }\,=\,100\,cd$

Beispiel 3: Spotlight

Spotlight

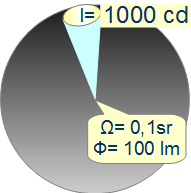
Verkleinert man den Raumwinkel des Scheinwerfer (aus Beispiel 2) ohne den Wert des erzeugten Lichtstroms Φ_v = 100 lm zu ändern, muss der Wert der Lichtstärke höhere Werte annehmen. (Bei kleinen Raumwinkeln bietet sich der Vergleich mit einem Spotlight an.) Konzentriert man den Lichtstrom Φ_v = 100 lm auf den Raumwinkel von Ω = 0,1 sr, ergibt sich eine Lichtstärke von I_v = 1000 cd. Die Formeln für dieses Beispiel:

$I_{\mathrm {v} }\,=\,{\frac {\Phi _{\mathrm {v} }}{\Omega }}\,;\qquad I_{\mathrm {v} }\,=\,{\frac {100\,lm}{0,1\,sr}}\,;\qquad I_{\mathrm {v} }\,=\,1000\,cd$

Lichtstärkemessung

Die Beschreibung eines einfachen Verfahrens zur Bestimmung der Lichtstärke bedient sich ebenfalls der fiktiven Kugel mit einem Meter Radius, in deren Mittelpunkt ein Leuchtmittel Licht erzeugt. Aus der Oberfläche dieser Kugel schneidet ein Raumwinkel der Größe ein Steradiant definitionsgemäß exakt die Fläche A von einem Quadratmeter aus. Über diesen einen Quadratmeter Kugeloberfläche lässt sich die Lichtstärke elegant mit der Beleuchtungsstärke verknüpfen, deren Definition ebenfalls die Bezugsfläche von einem Quadratmeter nutzt. Im Abstand von genau einem Meter zur Lichtquelle verteilt sich der Lichtstrom im Inneren des Raumwinkels $\textstyle \Omega =1sr$ auf eine Fläche A von einem Quadratmeter. Der Quotient aus Lichtstrom und Fläche A ergibt definitionsgemäß die Beleuchtungsstärke $\textstyle E_{\mathrm {v} }$ .

Im Abstand von genau einem Meter zur Lichtquelle lässt sich somit jede Beleuchtungsstärkemessung als Lichtstärkemessung interpretieren, weil die Bezugsflächen (jeweils ein Quadratmeter) identisch sind.

Beim Umfahren der Lichtquelle (im Abstand von einem Meter!) lässt sich der Zahlenwert (ohne Maßeinheit!) der Lichtstärke mit jedem handelsüblichen Luxmeter messtechnisch erfassen und die Abhängigkeit der Lichtstärke von Raumkoordinaten leicht überprüfen.

Die Lichtstärke ist neben dem Lichtstrom ein wesentliches Merkmal von Lichtquellen und bildet nicht zuletzt wegen des einfachen Messverfahrens eine der Basisgrößen des internationalen SI Systems!

Erläuterung

Die meisten Lichtquellen geben in unterschiedliche Richtungen unterschiedlich viel Licht ab.

Zur Beurteilung einer Lichtquelle ist nicht nur von Interesse, welchen Lichtstrom (gemessen in Lumen) die Quelle insgesamt abgibt, sie wird auch in verschiedene Richtungen verschieden viel Licht aussenden. Soll diese Richtungscharakteristik detailliert beschrieben werden, so ist das Konzept der Lichtstärke nötig.

Es ist nämlich nicht möglich anzugeben, wie viele Lumen in eine bestimmte Richtung abgegeben werden, da die endliche Anzahl abgestrahlter Lumen sich auf unendlich viele mögliche Richtungen verteilt und auf jede einzelne Richtung daher Null Lumen entfallen. Stattdessen betrachtet man einen kleinen, die gewünschte Richtung umgebenden Raumwinkel (gemessen in Steradiant), setzt den in diesen Raumwinkel abgegebenen (endlichen) Lichtstrom ins Verhältnis zur (endlichen) Größe des Raumwinkels und lässt den Raumwinkel gedanklich auf Null schrumpfen. Dabei streben sowohl der Raumwinkel als auch der in ihm enthaltene abgestrahlte Lichtstrom jeweils gegen Null, ihr Verhältnis aber gegen einen endlichen Grenzwert, die in die betreffende Richtung abgegebene Lichtstärke (gemessen in Lumen pro Steradiant oder gleichbedeutend Candela).

Dieser Grenzübergang entspricht beispielsweise auch jenem, der zur Bestimmung der Massendichte verwendet wird: Die in einem unendlich kleinen Volumen enthaltene Masse ist Null, aber der Quotient aus der in einem Volumen enthaltenen Masse und dem Volumen strebt bei Verkleinerung des Volumens gegen einen endlichen Grenzwert, die Massendichte des betrachteten Materials.

Definition

Exakte Definition

Die Lichtstärke in einer gegebenen Richtung ist nach obiger Erläuterung die Raumwinkeldichte des Lichtstromes in dieser Richtung. Gibt die Quelle in einen differentiellen Raumwinkel $\textstyle \mathrm {d} \Omega$ , welcher die betrachtete Richtung enthält, den differentiellen Lichtstrom $\textstyle \mathrm {d} \Phi _{\mathrm {v} }$ ab, so ist die Lichtstärke $\textstyle I_{\mathrm {v} }$ in dieser Richtung der Quotient aus den beiden differentiellen Größen:

$I_{{\mathrm {v}}}\,=\,{\frac {{\mathrm {d}}\Phi _{{\mathrm {v}}}}{{\mathrm {d}}\Omega }}$ .

Vereinfachte Definition

Falls die Lichtstärke in alle Richtungen, die in einen endlich großen Raumwinkel $\textstyle \Omega$ fallen, denselben Wert hat, dann erübrigt sich die Grenzwertbetrachtung und die differentielle Definition geht über in folgende vereinfachte Definition: Die Lichtstärke $\textstyle I_{\mathrm {v} }$ für alle Richtungen, die in den Raumwinkel $\textstyle \Omega$ fallen, ist der Quotient aus dem von der Lichtquelle in diesen Raumwinkel abgegebenen Lichtstrom $\textstyle \Phi _{\mathrm {v} }$ und dem durchstrahlten Raumwinkel $\textstyle \Omega$ :

$I_{{\mathrm {v}}}\,=\,{\frac {\Phi _{{\mathrm {v}}}}{\Omega }}$

Falls die Lichtstärke innerhalb des betrachteten endlichen Raumwinkels nicht konstant ist, kann die vereinfachte Definition dennoch verwendet werden. Das Ergebnis der Quotientenbildung ist dann der über den betreffenden Raumwinkel gebildete arithmetische Mittelwert der in den Raumwinkel fallenden Lichtstärken.

Einheit

→ Hauptartikel: Candela

In der Vergangenheit dienten unterschiedliche Lichtquellen als Bezugsgröße, zuletzt ein Hohlraumstrahler (Schwarzer Strahler): eine 1/600000 m² große Abstrahlfläche eines Hohlraumstrahlers bei der Erstarrungstemperatur des Platins und einem Umgebungsdruck von 101325 Pa strahlt in senkrechter Richtung Licht der Lichtstärke 1 cd ab.

Seit 1979 wird die Einheit Candela auf die abgeleitete SI-Einheit Watt zurückgeführt. Die aktuell gültige Definition

„Die Einheit 1 Candela ist die Lichtstärke in einer bestimmten Richtung einer Strahlungsquelle, die monochromatische Strahlung der Frequenz 540·10¹² Hz aussendet und deren Strahlstärke in dieser Richtung 1/683 W durch Steradiant beträgt.“

ist hierbei nicht als Realisierungsvorschrift zu verstehen (z.B. über die Verwendung von gelbgrüner Laserstrahlung).

Die angegebene Frequenz in Luft liegt nur zufällig in der Nähe des Maximums der Hellempfindlichkeit des 2° Standard-Beobachters. Vielmehr gibt die angegebene Frequenz den Schnittpunkt der beiden von der CIE definierten und vom BIPM veröffentlichten Hellempfindlichkeitskurven für photopisches Sehen (Tagsehen) und skotopisches Sehen (Nachtsehen) wieder, damit die Einheit Candela für beide Anregungszustände des menschlichen Auges gültig ist.

Eigenschaften

Die Lichtstärke ist die photometrische Entsprechung zur radiometrischen Strahlstärke. Ist die Strahlstärke der von einer Quelle in eine bestimmte Richtung abgegebenen elektromagnetischen Strahlung bekannt, so lässt sich daraus die entsprechende Lichtstärke ermitteln, indem die Beiträge der einzelnen Wellenlängen mit der jeweiligen spektralen Hellempfindlichkeit des Auges gewichtet werden. Die Lichtstärke beispielsweise einer Infrarot-Strahlungsquelle beliebiger Strahlungsintensität ist Null, da sie für das menschliche Auge unsichtbar ist.

Die Wahl der Lichtstärke als photometrische Basisgröße erscheint zunächst wenig nachvollziehbar, da man aus moderner Sicht etwa den Lichtstrom oder die Leuchtdichte als fundamentalere Größen ansehen würde.^{[Anm.
1]} Zur Anfangszeit der Photometrie jedoch, als der visuelle Vergleich von Lichtquellen im Vordergrund stand, war die Lichtstärke diejenige Eigenschaft der Quellen, die am einfachsten einem Vergleich zugänglich war und die daher als die fundamentale photometrische Größe eingeführt wurde.

Die Lichtstärke ist eine Eigenschaft der Lichtquelle und hängt nicht vom Abstand eines Beobachters ab. Das von der Quelle ausgesandte Licht „verdünnt“ sich zwar, während es sich von der Quelle entfernt, der in einen gegebenen Raumwinkel-Kegel abgestrahlte Lichtstrom bleibt dabei aber stets derselbe: Ein als Testfläche dienender Querschnitt durch den Raumwinkel-Kegel nimmt mit der Entfernung in demselbem Maße an Fläche zu wie der Lichtstrom sich „verdünnt“. Der die gesamte Fläche durchstrahlende Lichtstrom ist daher in allen Entfernungen derselbe und damit auch der Quotient aus dem Lichtstrom und dem Raumwinkel.

Dies steht nicht im Widerspruch dazu, dass ein Beobachter mit zunehmender Entfernung die Lichtquelle als „schwächer“ wahrnimmt. Für die Helligkeitswahrnehmung maßgeblich ist die Beleuchtungsstärke auf der Pupillenfläche^{[Anm.
2]} des Beobachterauges, also das Verhältnis des die Fläche durchstrahlenden Lichtstroms zur durchstrahlten Fläche. Entfernt sich das Auge von der Quelle, so bleibt die Größe der Empfängerfläche dieselbe, der die Fläche durchstrahlende Lichtstrom nimmt wegen seiner zunehmenden „Verdünnung“ jedoch ab. Im Abschnitt →Beleuchtungsstärke werden die betreffenden Berechnungsformeln erläutert.

Für eine Punktquelle beschreibt die Lichtstärke den mit einem „Lichtstrahl“ in eine gegebene Richtung transportierten Lichtstrom. Für eine flächenhafte Quelle beschreibt die Lichtstärke die Gesamtheit aller „Lichtstrahlen“, die von allen in diese Richtung strahlenden Punkten der Quelle ausgehen und – parallel zueinander verlaufend – den Lichtstrom in die gegebene Richtung transportieren.

Die Lichtstärke ist nicht nur für selbstleuchtende Lichtquellen definiert, sondern auch für reflektierende oder transmittierende Lichtquellen. Sie ist sogar an jedem Punkt des Raumes definiert, an dem Licht vorhanden ist. Man denke sich anstelle eines Licht abstrahlenden Oberflächenelements gegebenenfalls ein fiktives von Licht durchstrahltes Flächenelement im Raum.

Die vom Auge empfundene Helligkeit einer Lichtquelle stimmt nur bedingt mit der physikalischen Lichtstärke überein. Der Kontrast mit der Umgebung beeinflusst die physiologische Wahrnehmung. Eine Lichtquelle mit einer kleinen Oberfläche wird als heller (oder blendender) empfunden als eine Lichtquelle mit gleicher physikalischer Lichtstärke, aber einer größeren Oberfläche. Dieser Eindruck kann zum Beispiel bei Autoscheinwerfern verschiedener Größe oder bei Auf- oder Untergang von Mond oder Sonne beobachtet werden.

Zusammenhang mit anderen photometrischen Größen

Der Kürze halber werden im Folgenden hauptsächlich die vereinfachten, nichtdifferentiellen Ausdrücke verwendet. Falls die dafür nötigen Voraussetzungen nicht gegeben sind (wenn also insbesondere die Lichtstärke über den betrachteten Raumwinkel nicht konstant ist), müssen die entsprechenden Differentialquotienten oder Integrale angesetzt werden.

Lichtstrom

Öffnungswinkel α	Raumwinkel Ω
360°	(4π =) 12,566 sr
270°	10,726 sr
180°	(2π =) 6,283 sr
120°	(π =) 3,142 sr
90°	1,840 sr
65,541°	1 sr
60°	0,842 sr
45°	0,478 sr
30°	0,214 sr
10°	0,0239 sr
5°	0,00598 sr
2°	0,000957 sr
1°	0,000239 sr

Auflösen der Definitionsgleichung nach dem Lichtstrom liefert

$\Phi _{{{\mathrm {v}}\Omega }}\,=\,I_{{\mathrm {v}}}\cdot \Omega$

Der durch den Raumwinkel $\Omega$ tretende Lichtstrom $\Phi _{{{\mathrm {v}}\Omega }}$ ist also das Produkt aus der in den Raumwinkel gerichteten Lichtstärke und dem Raumwinkel. Falls die Lichtstärke innerhalb des betrachteten Raumwinkels variiert, bleibt das Ergebnis für den Lichtstrom exakt, wenn das arithmetische Mittel der Lichtstärken eingesetzt wird.

Die Form des Raumwinkels ist beliebig. Eine rechnerisch besonders einfach zu behandelnde Situation liegt vor, wenn ein durch eine kreisförmige Fläche aufgespannter Raumwinkel betrachtet wird. Die einen solchen Raumwinkel durchlaufenden Lichtstrahlen bilden einen Kreiskegel mit dem Öffnungswinkel $\alpha$ .^{[Anm.
3]} Der diesem Kegel entsprechende Raumwinkel beträgt

$\textstyle \Omega =2\pi \left(1-\cos \left({\frac {\alpha }{2}}\right)\right)$ Steradian.

Mit dieser Formel lässt sich der durchstrahlte Raumwinkel für Lichtquellen mit kegelförmiger Abstrahlcharakteristik berechnen. Die nebenstehende Tabelle enthält einige beispielhafte Zahlenwerte.

Die exakte Gleichung zur Berechnung des Lichtstroms aus der Verteilung der Lichtstärken in einem Raumwinkel $\Omega$ lautet:

$\Phi _{{{\mathrm {v}}\Omega }}\,=\,\int _{\Omega }{\mathrm {d}}\Phi _{{\mathrm {v}}}\,=\,\int _{\Omega }I_{{\mathrm {v}}}\,{\mathrm {d}}\Omega$ .

Beleuchtungsstärke

Gegeben sei eine Kugelkappe mit der Fläche und dem Kugelradius . Diese spannt bezogen auf das Zentrum der dazugehörigen Kugel den Raumwinkel $\textstyle \Omega \,=\,{\frac {A}{r^{2}}}$ auf. Die Beleuchtungsstärke $E_{{\mathrm {v}}}$ auf dieser Fläche ist der Quotient aus dem auf die Fläche auftreffenden Lichtstrom $\Phi_\mathrm{v}$ und der Fläche . Der auf die Fläche fallende Lichtstrom lässt sich ausdrücken als das Produkt der von der Lichtquelle in Richtung der betrachteten Fläche ausgesandten Lichtstärke $I_{{\mathrm {v}}}$ und dem von der Fläche aufgespannten Raumwinkel $\Omega$ . Berücksichtigt man noch den aus der Definition des Raumwinkels folgenden Zusammenhang $\Omega /A\,=\,1/r^{2}$ , so erhält man insgesamt:

$E_{{\mathrm {v}}}\,=\,{\frac {\Phi _{{\mathrm {v}}}}{A}}\,=\,{\frac {I_{{\mathrm {v}}}\cdot \Omega }{A}}\,=\,{\frac {I_{{\mathrm {v}}}}{r^{2}}}$

Die Beleuchtungsstärke hat der Formel entsprechend die Einheit Lumen durch Quadratmeter.^{[Anm.
4]} Diese Einheit trägt auch den Namen Lux.

Berücksichtigt man noch die Möglichkeit, dass die Empfangsfläche um den Winkel $\varepsilon$ gegen die Einstrahlrichtung geneigt ist,^{[Anm.
5]} so erhält man das photometrische Entfernungsgesetz:

$E_{{\mathrm {v}}}\,=\,{\frac {I_{{\mathrm {v}}}}{r^{2}}}\cdot \cos(\varepsilon )$

Wie zu erkennen ist, nimmt die von der Lichtquelle auf der Fläche erzeugte Beleuchtungsstärke mit dem Quadrat des Abstands ab, obwohl die von der Quelle in Richtung der Fläche ausgesandte Lichtstärke entfernungsunabhängig ist.

Diese Formel gilt nur für punktförmige Lichtquellen oder für hinreichend große Abstände. Andernfalls könnte ein Punkt der Empfangsfläche von Lichtstrahlen getroffen werden, die von verschiedenen Punkten der ausgedehnten Lichtquelle ausgehen und gegen denselben Punkt der Empfangsfläche konvergieren. Diese Lichtstrahlen wären nicht streng parallel und würden die Voraussetzung verletzen, dass die zu $I_{{\mathrm {v}}}$ beitragenden Lichtstrahlen in dieselbe Richtung ausgesandt wurden, also untereinander parallel sind. Darüber hinaus darf der Einfallswinkel $\varepsilon$ nicht zu stark über variieren.

Die Messung der Lichtstärke einer Quelle wird stets auf eine Messung der im Abstand erzeugten Beleuchtungsstärke zurückgeführt. Um die erwähnten Komplikationen nicht rechnerisch berücksichtigen zu müssen^{[Anm.
6]} und die obige einfache Formel verwenden zu können, wird die Messung in der Praxis in möglichst großem Abstand durchgeführt. Der Abstand, ab dem der Fehler bei Anwendung dieser Formel unter ein vorgegebenes Maß sinkt, heißt photometrische Grenzentfernung.

Die exakte Formel liefert dasselbe Ergebnis:

$E_{{\mathrm {v}}}\,=\,{\frac {{\mathrm {d}}\Phi _{{{\mathrm {v}}}}}{{\mathrm {d}}A}}\,=\,{\frac {I_{{\mathrm {v}}}\ {\mathrm {d}}\Omega }{{\mathrm {d}}A}}\,=\,{\frac {I_{{\mathrm {v}}}}{r^{2}}}$

Ergänzung um den Cosinus des Einfallswinkels (sofern nötig) ergibt wieder die obige Formel.

Leuchtdichte

Die Definition der Leuchtdichte $L_{{\mathrm {v}}}$ entspricht im Wesentlichen jener der Lichtstärke. Während die in eine bestimmte Richtung gerichtete Lichtstärke jedoch alle von der Lichtquelle in diese Richtung gesandten Lichtstrahlen umfasst, berücksichtigt die Leuchtdichte nur die in diese Richtung und von einem bestimmten Flächenelement ausgesandten Strahlen. Sendet die Fläche unter dem Abstrahlwinkel $\varepsilon$ Licht in eine gegebene Richtung, so ist ihre Leuchtdichte in dieser Richtung gleich dem Quotienten aus der Lichtstärke der Lichtquelle in dieser Richtung und der in Strahlrichtung projizierten Abstrahlfläche:

$L_{{\mathrm {v}}}\,=\,{\frac {I_{{\mathrm {v}}}}{A\ \cos(\varepsilon )}}\,=\,{\frac {\Phi _{{\mathrm {v}}}}{A\ \cos(\varepsilon )\cdot \Omega }}$ .

In der exakten Formulierung lautet der Zusammenhang:

$L_{{\mathrm {v}}}\,=\,{\frac {{\mathrm {d}}I_{{\mathrm {v}}}}{{\mathrm {d}}A\ \cos(\varepsilon )}}\,=\,{\frac {{\mathrm {d^{2}}}\Phi _{{\mathrm {v}}}}{{\mathrm {d}}A\ \cos(\varepsilon )\cdot {\mathrm {d}}\Omega }}$ .

Rechenbeispiele

Beispiel 1

Eine Lichtquelle erzeuge einen Lichtstrom von 12 Lumen und strahle dieses Licht isotrop ab, d.h. die Lichtstärke sei in allen Richtungen dieselbe. Wie groß ist die Lichtstärke der Quelle in einer beliebigen gegebenen Richtung?

Aufgrund der vorausgesetzten Konstanz der Lichtstärke kann die vereinfachte Formel $\Phi _{{{\mathrm {v}}\Omega }}\,=\,I_{{\mathrm {v}}}\cdot \Omega$ verwendet werden. Auflösen nach $I_{{\mathrm {v}}}$ liefert $I_{{\mathrm {v}}}\,=\,\Phi _{{{\mathrm {v}}\Omega }}/\Omega$ . Der volle die Lichtquelle umgebende Raumwinkel beträgt 4π Steradiant. Der Lichtstrom von 12 Lumen verteilt sich gleichmäßig auf den Raumwinkel von 4π Steradiant, die Lichtstärke beträgt daher 12 Lumen pro 4π Steradiant ≈ 1 Lumen pro Steradiant = 1 Candela.

Eine solche Lichtquelle entspricht ungefähr einer freistehenden Haushaltskerze, wenn die Abschattung der Flamme durch den Kerzenkörper nach unten hin und seine Reflektorwirkung nach oben, sowie das Flackern der Intensität vernachlässigt werden.

Dieselbe Lichtquelle werde nun mit einer scheinwerferartigen Fokussiereinrichtung versehen, so dass das gesamte erzeugte Licht gleichmäßig innerhalb eines Kreiskegels mit einem Öffnungswinkel α von 5° abgegeben wird. Wie groß ist die Lichtstärke der Quelle in einer innerhalb des Abstrahlkegels gelegenen Richtung?

Der Kegel spannt den Raumwinkel 0,006 Steradiant auf (s. obige Tabelle). Da die Lichtstärke als innerhalb dieses Raumwinkels konstant vorausgesetzt wird, kann wieder die vereinfachte Formel verwendet werden. Die Lichtstärke für alle innerhalb des Kegels gelegenen Richtungen beträgt demnach 12 Lumen pro 0,006 Steradiant, also 2000 Lumen pro Steradiant oder 2000 Candela. Für alle anderen Richtungen beträgt sie Null Candela. Durch Fokussierung konnte die Lichtstärke der Quelle also in bestimmten Richtungen (und auf Kosten anderer Richtungen) erhöht werden.

Wird das Licht nicht gleichmäßig innerhalb des Kegels abgegeben, so sind die Lichtstärken für die in den Kegel fallenden Richtungen unterschiedlich und es müssen entweder die exakten Formeln verwendet werden, oder man begnügt sich unter Verwendung der vereinfachten Formeln mit der Ermittlung eines Mittelwertes.

Beispiel 2

Lambert-Strahler

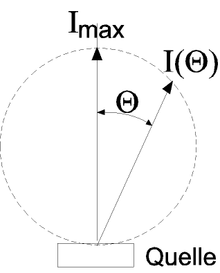
Ein Lambert-Strahler (auch: diffuser Strahler) ist ein Strahler, der in alle Abstrahlrichtungen Licht mit derselben Leuchtdichte abgibt.

Gegeben sei eine ebene Abstrahlfläche der Größe 1 m², welche über die ganze Fläche und in allen Richtungen gleichmäßig mit der Leuchtdichte $L_{{\mathrm {v}}}$ = 1000 cd/m² strahlt. Mit welcher Lichtstärke strahlt sie in senkrechter Richtung (0°) ab? Wie groß ist die Lichtstärke in den Abstrahlrichtungen 45° und 90°?

Da die Leuchtdichte als über die Fläche konstant vorausgesetzt wird, kann die vereinfachte Formel $L_{{\mathrm {v}}}\,=\,I_{{\mathrm {v}}}/(A\ \cos(\varepsilon ))$ verwendet werden. Da die Leuchtdichte als in allen Richtungen identisch vorausgesetzt wird, kann sie als richtungsunabhängige Konstante behandelt werden. Auflösen der Gleichung nach $I_{{\mathrm {v}}}$ liefert:

$I_{{\mathrm {v}}}\,=\,L_{{\mathrm {v}}}\cdot A\ \cos(\varepsilon )$

Einsetzen der Zahlenwerte ergibt:

$\varepsilon$	$L_{{\mathrm {v}}}$	$A\ \cos(\varepsilon )$	$I_{{\mathrm {v}}}$
90°	1000 cd/m²	1 m²	1000 cd
45°	1000 cd/m²	0,707 m²	707 cd
0°	1000 cd/m²	0 m²	0 cd

Ein solcher diffuser Strahler könnte z.B. durch ein entsprechend beleuchtetes weißes Blatt Papier dargestellt werden. Das Auge nimmt die Leuchtdichte als Flächenhelligkeit wahr. Der Umstand, dass das Papier nach Voraussetzung diffus strahlt, also in alle Richtungen dieselbe Leuchtdichte abgibt, bedeutet für den Betrachter, dass es aus allen Richtungen betrachtet dieselbe Flächenhelligkeit aufweist. Da es aber bei schräger Betrachtung um den Projektionsfaktor cos(ε) verkürzt erscheint (also einen kleineren Raumwinkel einnimmt) erreicht den Betrachter trotz gleich gebliebener Flächenhelligkeit eine geringere Lichtmenge: die Lichtstärke in dieser Richtung ist geringer.

Eine Lichtquelle wird als anisotrop bezeichnet, wenn ihre Lichtstärke abhängig von der Betrachtungsrichtung ist. Im vorliegenden Fall ergibt sich die Anisotropie bei gleich bleibender Leuchtdichte allein aus dem Projektionseffekt. Bei den meisten Lichtquellen ist auch die Leuchtdichte richtungsabhängig. Die Abhängigkeit der Lichtstärke vom Betrachtungswinkel wird auch als Abstrahlcharakteristik bezeichnet.

Die Abstrahlcharakteristik der isotropen Hauskerzen-Flamme ist kugelförmig und die des Lambertschen Strahlers folgt der mathematischen Funktion $I_{\theta }=I_{\max }\cos \ (\theta )$ . Die exakten Abstrahlcharakteristiken realer Lichtquellen (z.B. Taschenlampe) werden teilweise durch die Hersteller zur Verfügung gestellt.

Beispiele für Lichtstärken verschiedener Lichtquellen

Lichtquelle	Lichtstärke
Glühwürmchen	0,0002 cd
Kerze (in allen Richtungen)	ca. 1 cd
Glühlampe 100 W (in allen Richtungen)	ca. 100 cd
Grüner Laserpointer, 532 nm, 5 mW, 1,0 mrad Divergenz (in Strahlrichtung)	3,8·10⁶ cd
Leuchtfeuer Helgoland (in Strahlrichtung)	40·10⁶ cd
Sonne (in allen Richtungen)	3,0·10²⁷ cd

Veraltete Einheiten

Früher übliche Lichtstärkeeinheiten waren:

die Alte Lichteinheit, definiert durch eine 83 g schwere Wachskerze mit einer Flammenhöhe von 42 mm
die Einheit des Deutschen Vereins der Gas- und Wasserfachmänner, DVGW, definiert durch eine Paraffinkerze von 20 mm Durchmesser bei 50 mm Flammenhöhe
die Berliner Lichteinheit, definiert durch eine Walrat-Kerze mit 44,5 mm Flammenhöhe und einem Verbrauch von 7,77 g pro Stunde
die Violle-Einheit, benannt nach dem französischen Physiker Jules Violle, 1889 definiert als die Lichtstärke eines Quadratzentimeters Platin bei einer Verfestigungstemperatur von 2042 Kelvin,
die „bougie décimale“ war vor 1901 in Frankreich eine Maßeinheit der Lichtstärke und wurde 1909 als „Internationale Kerze“ (IK) von Großbritannien und den USA übernommen
ab 1896 wurde in Deutschland die Hefnerkerze (HK) verwendet

Alle Einheiten wurden 1942 durch die „Neue Kerze“ (NK) ersetzt, die 1948 in Candela umbenannt wurde und seitdem als SI-Basiseinheit für die Lichtstärke gilt.

Vergleichswerte der Lichtstärken-Einheiten
Neue Kerze (NK) / Candela	Hefnerkerze (HK)	Internationale Kerze (IK)	Berliner LE	DVGW-Kerze	Violle
1	1,1074	0,98	0,9014	0,9225	0,04907
0,9030	1	0,8860	0,8140	0,8330	0,04433
1,0190	1,1280	1	0,9187	0,9402	0,05000
1,11	1,2278	1,0885	1	1,0233	0,05442
1,08	1,1998	1,0636	0,9772	1	0,05318
20,38	22,5600	20,0000	18,3747	18,8036	1

Übersicht über die photometrischen Größen

Übersicht über photometrische Größen und Einheiten
Bezeichnung	Formelzeichen	Definition	Einheitenname	Einheitenumformung	Dimension
Lichtstrom (luminous flux, luminous power)	$\textstyle \mathit{\Phi_\mathrm{v}}\,, F\,, P$	$\textstyle \mathit{\Phi_\mathrm{v}} = K_\mathrm{m}\int_{380\,\mathrm{nm}}^{780\,\mathrm{nm}}\frac{\partial\mathit{\Phi_\mathrm{e}}(\lambda)}{\partial \lambda}\cdot V(\lambda)\,\mathrm{d}\lambda$	Lumen (lm)	$\textstyle \mathrm{1\, lm = 1\, sr \cdot cd}$	$\mathsf{J} \,$
Beleuchtungsstärke (illuminance)	$\textstyle E_\mathrm{v} \,$	$\textstyle E_\mathrm{v}=\frac{\partial \mathit{\Phi_\mathrm{v}}}{\partial A}$	Lux (lx), früher auch Nox (nx), Phot (ph)	$\textstyle \mathrm{1\, lx = 1\,\frac{lm}{m^2} = 1\,\frac{sr \cdot cd}{m^2}}$	$\mathsf{L^{-2} \cdot J}$
Spezifische Lichtausstrahlung (luminous emittance)	$\textstyle M_\mathrm{v} \,$	$\textstyle M_\mathrm{v}=\frac{\partial \mathit{\Phi_\mathrm{v}}}{\partial A}$	Lux (lx)	$\textstyle \mathrm{1\, lx = 1\,\frac{lm}{m^2} = 1\,\frac{sr \cdot cd}{m^2}}$	$\mathsf{L^{-2} \cdot J}$
Leuchtdichte (luminance)	$\textstyle L_\mathrm{v} \,$	$\textstyle L_\mathrm{v}=\frac{\partial^2 \mathit{\Phi_\mathrm{v}}}{\partial \Omega \cdot \partial A_1 \cdot \cos \varepsilon_1}$	keine eigene Einheit, manchmal Nit genannt, früher auch in Stilb (sb), Apostilb (asb), Lambert (la), Blondel	$\textstyle \mathrm{1\,\frac{cd}{m^2} = 1\,\frac{lm}{sr \cdot m^2}}$	$\mathsf{L^{-2} \cdot J}$
Lichtstärke (luminous intensity)	$\textstyle I_\mathrm{v} \,$	$\textstyle I_\mathrm{v}=\frac{\partial\mathit{\Phi_\mathrm{v}}}{\partial\Omega}$	Candela (cd) (SI-Basiseinheit), früher auch Hefnerkerze (HK), Internationale Kerze (IK), Neue Kerze (NK)	$\textstyle \mathrm{1\, cd = 1\, \frac{lm}{sr}}$	$\mathsf{J} \,$
Lichtmenge (luminous energy)	$\textstyle Q_\mathrm{v} \,$	$\textstyle Q_\mathrm{v}= \int_{0}^{T} \mathit{\Phi_\mathrm{v}}(t) \mathrm{d}t$	Lumensekunde (lm s), Talbot, Lumberg	$\textstyle \mathrm{1\, lm \cdot s = 1\, sr \cdot cd \cdot s}$	$\mathsf{T \cdot J}$
Belichtung (luminous exposure)	$\textstyle H_\mathrm{v} \,$	$\textstyle H_\mathrm{v}= \int_{0}^{T} E_\mathrm{v}(t) \mathrm{d}t$	Luxsekunde (lx s)	$\textstyle \mathrm{1\, lx \cdot s = 1\,\frac{lm \cdot s}{m^2} = 1\,\frac{sr \cdot cd \cdot s}{m^2}}$	$\mathsf{L^{-2} \cdot T \cdot J}$
Lichtausbeute (luminous efficacy)	$\textstyle \eta\,, \rho\,$	$\textstyle \eta=\frac{\mathit{\Phi_\mathrm{v}}}{P}$	Lumen / Watt	$\textstyle \mathrm{1\,\frac{lm}{W} = 1\,\frac{sr \cdot cd \cdot s}{J} = 1\, \frac{sr \cdot cd \cdot s^2}{kg \cdot m^2}}$	$\mathsf{M^{-1} \cdot L^{-2} \cdot T{^3} \cdot J}$
Raumwinkel (solid angle)	$\textstyle \Omega \,$	$\textstyle \Omega = \frac{S}{r^2}$	Steradiant (sr)	$\textstyle \mathrm{1\, sr = \frac{\left[ Fl\ddot{a}che \right]}{\left[ Radius^2 \right]} = 1\,\frac{m^2}{m^2}}$	$\mathsf{1} \,$ (Eins)

Siehe auch

Lichtstärke (Fotografie)

Anmerkungen

↑ Der Lichtstrom ist eine integrale Größe, aus der sich alle anderen photometrischen Größen durch Differenzieren ableiten lassen. Die Leuchtdichte ist eine differentielle Größe, aus der sich alle anderen photometrischen Größen durch Integration ableiten lassen.
↑ Genauer: die Beleuchtungsstärke auf der Netzhaut, die aber bei gegebener Pupillenöffnung und gegebenem Transmissionsgrad der Augenmedien durch die Beleuchtungsstärke auf der Pupillenfläche festgelegt ist, vgl. DIN 5031: Strahlungsphysik im optischen Bereich und Lichttechnik. Teil 6: Pupillen-Lichtstärke als Maß für die Netzhautbeleuchtung., Beuth-Verlag, Berlin 1982.
↑ Gemeint ist der von einer Seite des Kegelmantels bis zur gegenüberliegenden Seite gezählte „volle“ Öffnungswinkel, nicht der „halbe“ Öffnungswinkel zwischen Kegelachse und Kegelmantel.
↑ Der im I_v vorkommende Steradiant entspricht einer dimensionslosen Eins.
↑ $\varepsilon$ ist der Winkel zwischen der Flächennormalen und der Strahlungsrichtung.
↑ Dies geschähe durch Integration über Sender- und Empfangsfläche unter Anwendung des photometrischen Grundgesetzes.

Basierend auf einem Artikel in:

Wikipedia.de