Stetigsinguläre Wahrscheinlichkeitsverteilung
Eine stetigsinguläre (Wahrscheinlichkeits)verteilung ist eine spezielle Wahrscheinlichkeitsverteilung in der Stochastik, die sich durch ihre Irregularität auszeichnet. So besitzen stetigsinguläre Wahrscheinlichkeitsverteilungen weder eine Darstellung durch eine Wahrscheinlichkeitsfunktion noch durch eine Wahrscheinlichkeitsdichtefunktion, besitzen aber trotzdem eine stetige Verteilungsfunktion.
Stetigsinguläre Verteilungen treten selten auf oder müssen extra konstruiert werden. Beispiel hierfür ist die Cantor-Verteilung
Definition
Gegeben sei eine Wahrscheinlichkeitsverteilung
auf
.
Dann heißt
eine stetigsinguläre Wahrscheinlichkeitsverteilung, wenn
ein atomloses
Maß ist und singulär
bezüglich des Lebesgue-Maßes.
Voll ausgeschrieben bedeutet das:
- Für alle
ist
(atomlos)
- Es existiert ein
mit
und
(Singularität)
Beispiel
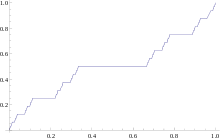
Typisches Beispiel einer stetigsingulären Verteilung ist die Cantor-Verteilung,
deren Verteilungsfunktion rechts abgebildet ist. Die exakte Konstruktion ist im
Hauptartikel zur Cantor-Verteilung erklärt und hängt eng mit der Cantor-Menge
zusammen.
Zu beachten ist, dass die Verteilungsfunktion stetig ist, woraus folgt, dass
die Cantor-Verteilung keinen diskreten Anteil hat bzw. atomlos ist. Denn jedes
Atom, also jedes
mit
würde sich als Sprungstelle der Verteilungsfunktion äußern.
Des Weiteren ist die Verteilungsfunktion aufgrund ihrer Konstruktion auf dem
Komplement der Cantor-Menge
konstant. Daraus folgt, dass
.
Da die Cantor-Menge selbst aber das Lebesgue-Maß 0 hat, also
gilt, sind die Cantor-Verteilung und das Lebesgue-Maß singulär zueinander.
Somit ist die Cantor-Verteilung atomlos und singulär zu Lebesgue-Maß, also stetigsingulär.
Eigenschaften
- Wie oben bereits erwähnt besitzt eine stetigsinguläre Verteilung weder eine Wahrscheinlichkeitsdichtefunktion noch eine Wahrscheinlichkeitsfunktion, aber eine stetige Verteilungsfunktion.
- Aufgrund der Nicht-Existenz der Wahrscheinlichkeits(dichte)funktion existiert der Modus nicht.
- Nach der Lebesgue-Zerlegung lässt sich jede Wahrscheinlichkeitsverteilung zerlegen in eine diskrete Wahrscheinlichkeitsverteilung (mit Wahrscheinlichkeitsfunktion), eine absolutstetige Wahrscheinlichkeitsverteilung (mit Wahrscheinlichkeitsdichtefunktion) und eine stetigsinguläre Wahrscheinlichkeitsverteilung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.01. 2018