Innere-Punkte-Verfahren

Innere-Punkte-Verfahren nähern sich einer Optimallösung durch das Innere des Polyeders.

Innere-Punkte-Verfahren sind in der Optimierung eine Klasse von Algorithmen zur Lösung von Optimierungsaufgaben. Ihr Hauptanwendungsgebiet sind lineare oder quadratische Programme. Sie werden aber auch zur Lösung (allgemeiner) nichtlinearer Programme, semidefinierter Programme oder Komplementaritätsproblemen eingesetzt.

Im Vergleich zu den traditionelleren Active-Set-Methoden (z.B. Simplex-Verfahren) zeichnen sich Innere-Punkte-Verfahren durch bessere theoretische Eigenschaften (polynomiale Komplexität) und schnellere Konvergenz für sehr große dünnbesetzte Probleme aus. Ein Nachteil ist, dass sie vergleichbar ungeeignet zum Lösen einer Serie von Optimierungsaufgaben sind (was für viele Algorithmen der ganzzahligen Optimierung, wie z.B. Branch and Bound oder Schnittebenenverfahren, wichtig ist).

Aufgabenstellung

Im einfachsten Fall werden Innere-Punkte-Verfahren benutzt, um das lineare Problem

$\min _{x}c^{T}x,{\mathrm {~wobei~}}Ax=b,x\geq 0$

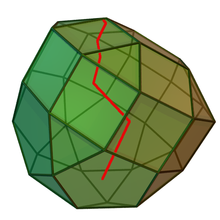
zu lösen. Dabei ist A eine $m\times n$ -Matrix, und c, b sind jeweils n- bzw. m-dimensionale Vektoren. Die zulässige Menge $X=\{x:Ax=b,\,x\geq 0\}$ hat die Form eines Polyeders. Aus der Theorie der linearen Optimierung ist bekannt, dass eine optimale Lösung des Optimierungsproblems in einer der Ecken des Polyeders angenommen wird. Im Gegensatz zum Simplex-Verfahren, das sich entlang der Kanten von Ecke zu Ecke bewegt, versuchen Innere-Punkte-Verfahren einen Pfad zum Optimum durch das „Innere“ des Polyeders zu finden.

Geschichte

Logarithmische-Barriere-Verfahren wurden erstmals von Ragnar Anton Kittil Frisch (1956) beschrieben. Als wichtige frühe Referenz zum Thema Barriere-Verfahren gilt Fiacco und McCormick (1968). Sie galten damals jedoch als ineffizient und (durch das Logarithmieren sehr kleiner Zahlen) als numerisch instabil. Als Geburtsstunde der Inneren-Punkte-Verfahren gilt gemeinhin die Arbeit von Narendra Karmarkar von 1984, in der er zum ersten Mal einen polynomialen potentiell praktisch einsetzbaren Algorithmus für lineare Probleme beschreibt. Dieser Algorithmus wies schon viele Gemeinsamkeiten zu den modernen Verfahren auf, auch wenn die bedeutenden Durchbrüche, die Innere-Punkte-Verfahren zu einer echten Konkurrenz für das Simplex-Verfahren machten, erst in den 1990er Jahren geschahen (z.B. Mehrotra (1992)).

Herleitung

Vom heutigen Standpunkt aus gibt es verschiedene Wege, um Innere-Punkte-Verfahren zu motivieren. Eine Möglichkeit ist über Logarithmische Barrieren: Hierbei werden die Positivitätsbedingungen $x\geq 0$ durch logarithmische Strafterme $-\mu \ln x_{i}$ in der Zielfunktion ersetzt (hierbei ist $\mu>0$ ein Parameter). Anstatt des Ursprungsproblems löst man also

$\min _{x}c^{T}x-\mu \sum _{i}^{n}\ln x_{i}{\mathrm {~wobei~}}Ax=b$

Für kleine Werte von wird $-\ln x$ sehr groß, man versucht also durch Bestrafung kleiner x-Werte die Lösung des Optimierungsproblems im Inneren der Menge der positiven Koordinaten zu halten. Diese Bestrafung wird umso kleiner, je kleiner der Parameter $\mu$ ist. Im Grenzwert $\mu \to 0$ erwartet man, dass die Lösung des Barriereproblems gegen die Lösung des Ursprungsproblems konvergiert. Das Barriereproblem ist ein (streng) konvexes Problem, seine (einzige, globale) Lösung findet man durch Anwendung des lagrangeschen Multiplikatorensatz als Lösung des (nichtlinearen) Gleichungssystems

${\begin{matrix}Ax&=&b\\A^{T}y+s&=&c\\x_{i}s_{i}&=&\mu \\x,s&\geq &0\end{matrix}}$

Hierbei entspricht die erste Zeile der Zulässigkeit bezüglich des Primalen Problems, die zweite Zeile der Zulässigkeit bezüglich des Dualen Problems nach der Einführung von Schlupfvariablen und die dritte Zeile dem komplementären Schlupf. Für jeden Wert $\mu \geq 0$ ist dieses Gleichungssystem eindeutig lösbar. Die Menge aller Lösungen für verschiedene $\mu$ beschreibt einen Pfad (den zentralen Pfad), der das Analytische Zentrum des zulässigen Polyeders (für $\mu =\infty$ ) mit der Lösung des Ursprungsproblems (für $\mu =0$ ) verbindet. Algorithmisch kann das Gleichungssystem per Newton-Verfahren gelöst werden. In Innere-Punkte-Verfahren wird nach jeder Iteration des Newton-Verfahrens der Parameter $\mu$ reduziert. Durch geeignete Heuristiken wird sichergestellt, dass die Konvergenz von $\mu \to 0$ und die des Newton-Verfahrens synchron ablaufen.

Eigenschaften

Innere-Punkte-Verfahren sind global konvergent.
Die Kurzschrittvariante des Innere-Punkte-Verfahrens braucht im ungünstigsten Fall ${\mathcal {O}}\left({\frac {1}{\varepsilon }}{\sqrt {n}}\right)$ Iterationen, um die Lösung eines linearen Problems mit Genauigkeit $\varepsilon$ zu finden. Dies ist zurzeit die beste bekannte theoretische Schranke. Das Kurzschrittverfahren ist in der Praxis anderen Varianten jedoch unterlegen.
In der Praxis beobachtet man $\mathcal{O}(\log n)$ Iterationen.

Algorithmus

Wähle primale und duale Startvektoren .
Setze $\mu _{{alt}}=x^{T}s/n$
Reduziere $\mu :0<\mu _{{\operatorname {neu}}}<\mu _{{\operatorname {alt}}}$ .
Berechne die Newton-Richtung durch Lösen des linearen Gleichungssystems: ${\begin{bmatrix}0&A^{T}&I\\A&0&0\\S&0&X\end{bmatrix}}{\begin{bmatrix}\Delta x\\\Delta y\\\Delta s\end{bmatrix}}={\begin{bmatrix}c-A^{T}y-s\\b-Ax\\\mu _{{\operatorname {neu}}}e-XSe\end{bmatrix}}$ (dabei sind Diagonalmatrizen, auf deren Diagonale die Elemente der Vektoren x, s stehen, sowie $e=(1,\ldots ,1)^{T}$ ).
Wähle eine Schrittweite $\alpha >0$ , so dass $x+\alpha \Delta x>0,s+\alpha \Delta s>0$ komponentenweise gilt. Einige Varianten des Innere-Punkte-Verfahrens stellen weitere Bedingungen an $\alpha$ .
Setze $x\leftarrow x+\alpha \Delta x,y\leftarrow y+\alpha \Delta y,s\leftarrow s+\alpha \Delta s$
Zurück zu Schritt 2

Varianten des Verfahrens und Umgebungen

Es gibt mehrere Varianten von Innere-Punkte-Verfahren, die sich im Wesentlichen in der Wahl von $\mu _{{\operatorname {neu}}}$ und $\alpha$ unterscheiden. Die wichtigsten sind Kurzschrittverfahren, Langschrittverfahren und Predictor-Corrector-Verfahren (Vorhersage und Korrektur). Um sie zu beschreiben, werden die folgenden Umgebungen des zentralen Pfades benötigt:

${\mathcal {N}}_{2}(\theta )=\{(x,y,s)\in {\mathcal {F}}^{0}:\|XSe-\mu e\|_{2}\leq \theta \mu \}$

und

${\mathcal {N}}_{{-\infty }}(\gamma )=\{(x,y,s)\in {\mathcal {F}}^{0}:x_{i}s_{i}\geq \gamma \mu ,i=1,\ldots ,n\}$

dabei ist ${\mathcal {F}}^{0}=\{(x,y,s):Ax=b,A^{T}y+s=c,x>0,s>0\}$ das Innere der zulässigen Menge. Der zentrale Pfad ist durch die Bedingung $x_{i}s_{i}=\mu$ definiert. In der ${\mathcal {N}}_{2}$ -Umgebung wird die Euklidische Norm der Abweichung des Vektors $(x_{1}s_{1},\ldots ,x_{n}s_{n})$ von $(\mu ,\ldots ,\mu )$ beschränkt, bei der ${\mathcal {N}}_{{-\infty }}$ -Umgebung wird lediglich verlangt, dass die Produkte $x_{i}s_{i}$ nicht zu klein werden.

Die Varianten des Innere-Punkte-Verfahrens sind im Einzelnen:

Kurzschrittverfahren: Für. geeignete Parameter $\theta ,\beta$ wird $\mu _{{\operatorname {neu}}}=(1-\beta /{\sqrt {n}})\mu _{{\operatorname {alt}}}$ und $\alpha =1$ gesetzt. Wenn der Startpunkt in ${\mathcal {N}}_{2}(\theta )$ ist, so gilt dies auch für alle weiteren Iterationspunkte.
Langschrittverfahren: $\gamma \in (0,1),0<\sigma _{{\min }}<\sigma _{{\max }}<1$ werden gewählt. Es wird $\mu _{{\operatorname {neu}}}=\sigma _{k}\mu _{{\operatorname {alt}}}$ mit $\sigma _{k}\in (\sigma _{{\min }},\sigma _{{\max }})$ gesetzt und $\alpha$ so gewählt, dass zusätzlich $(x,y,s)\in {\mathcal {N}}_{{-\infty }}(\gamma )$ gilt.
Predictor-Corrector-Verfahren: Es wird zuerst $\mu _{{\operatorname {neu}}}=0$ gewählt, und das maximale $\alpha$ für diesen Fall bestimmt (Predictor). Dieses $\alpha$ liefert einen Schätzwert für das optimale $\mu _{{\operatorname {neu}}}$ , das nun im zweiten Schritt gewählt wird. Im zweiten Schritt wird außerdem versucht, den Linearisierungsfehler der dritten Gleichung ( $XSe=\mu e$ ) durch das Newton-Verfahren zu korrigieren. Im Predictor-Corrector-Verfahren wird das obige Newton-Gleichungssystem für zwei verschiedene rechte Seiten gelöst. Es ist möglich, dies sehr effizient zu implementieren (Cholesky-Zerlegung).

Das Predictor-Corrector-Verfahren ist den anderen Varianten in der Praxis überlegen, ist jedoch schwerer zu analysieren und besitzt schlechtere theoretische Eigenschaften.

Basierend auf einem Artikel in:

Wikipedia.de