
Spinelle

Die Spinell-Supergruppe, auch Spinellobergruppe bzw. Spinell-Obergruppe oder kurz Spinelle, umfasst Minerale des chemischen Verbindungstyps AB2X4, die in der Spinellstruktur kristallisiert sind. In dieser Formel sind A und B Metallkationen und X die Anionen O2-, S2- und Se2-. Synthetisch sind noch Spinelle mit den Anionen N3- (z. B. SiTi2NF4), Te2- (z. B. Cr2+Cr3+2Te4), Cl- (z. B. ZnLi2Cl4), F- (z. B. NiLi2F4) und (CN)- (z. B. ZnK2(CN)4) bekannt.
In der Spinellstruktur bilden die X-Anionen eine annähernd kubisch dichteste Kugelpackung, in der 1/8 der Tetraederlücken (umgeben von 4 Anionen) und die Hälfte der Oktaederlücken (umgeben von 6 Anionen) mit Kationen besetzt sind.
Aufgrund der hohen, kubischen Symmetrie ist die Spinellstruktur recht starr. Sie enthält nur drei unterschiedliche Gitterpositionen und wird durch nur 2 variable Parameter beschrieben. Dennoch ist die Bandbreite der Zusammensetzungen erstaunlich hoch. Über 200 Verbindungen mit Spinellstruktur sind bekannt, davon kommen 61 (Stand 2023) natürlich vor. Die Kationenpositionen werden von rund 36 verschiedenen Ionen (Leerstellen inklusive) mit Ladungen zwischen 0 (Leerstelle) und +6 besetzt.[1]
Spinelle bilden meist oktaedrische Kristalle. Oxispinelle sind transparent und je nach Zusammensetzung farblos bis gelblich, grün, blau, violett, rot oder schwarz und opak. Sie zeigen Glasglanz und sind mit einer Mohshärte von 5 bis 8 recht hart. Thio- und Selenospinelle sind opak mit einem silbrig-grauen bis messing- oder bronzefarbenen Metallglanz und von geringerer Härte (2,5 - 5).
Minerale der Spinell-Supergruppe bilden sich unter verschiedensten Bedingungen zu allen Phasen der Entwicklung unseres Sonnensystems. Sie gehören zu den ersten Kondensaten aus dem präsolaren Nebel (Spinell) und sind schon von Mireille Christophe Michel-Lévy bei der ersten Beschreibung eines Calcium-Aluminium-reichen Einschlusses in einem Chondriten gefunden worden. Sie bilden sich magmatisch durch Kristallisation z. B. aus basischen und ultrabasischen Schmelzen (Chromit, Magnesiochromit, Ulvöspinell) sowie metasomatisch und metamorph. Spinelle finden sich im oberen Erdmantel (Spinell-Peridotit) und in der Mantelübergangszone in einer Tiefe zwischen 500 und 660 km liegt die Verbindung Mg2SiO4, die einen Großteil des Erdmantels ausmacht, in der Spinellstruktur (Ringwoodit) vor. Viele Spinelle sind sehr hart und verwitterungsbeständig und reichern sich daher in Sedimenten wie Schwermineralsanden und Seifen an.
Geschichte

Die magnetischen Eigenschaften des Spinells Magnetit haben die Menschen seit der Antike fasziniert und Magnetit gehört zu den ersten magnetischen Werkstoffen, die Menschen genutzt haben. Thales von Milet war um 585 v.Chr. in Europa der erste, der die Beobachtung dokumentierte, dass der Magneteisenstein, wahrscheinlich Magnetit, Objekte aus Eisen anzieht, was er Aristoteles zufolge einer „Seele“ zuschrieb, in der Thales die Ursache aller Bewegung vermutete.[2][3]

Die erste Schilderung magnetischen Verhaltens vermutlich von Magnetit in chinesischen Überlieferungen stammt aus einer Textsammlung aus dem 4. Jahrhundert v.Chr.[4] und seit der Han-Dynastie (202 v.Chr. – 220 n.Chr.) ist mit dem „Si Nan“, dem nach Süden zeigenden Löffel, der erste Kompass bekannt. Er diente vermutlich nur zu geomantischen Zwecken, z. B. zur Ausrichtung von Gebäuden und Wegen nach der Richtung des Flusses des Qi, in Nord-Süd-Richtung.[4][5][6]
Transparente Spinelle sind begehrte Schmucksteine und zahlreiche „Rubine“ diverser Kronjuwelen sind rote Spinelle, z. B. der Samarian Spinel der persischen Kronjuwelen, der Black Prince´s Ruby der Imperial State Crown oder der Rubin der Spitze der russischen Zarenkrone.

Die Spinellobergruppe sowie die Spinellgruppe wurden nach dem ersten bekannten Mineral dieser Gruppen benannt, dem Spinell. Schriftlich überliefert ist der Name Spinell in unterschiedlicher Schreibweise seit dem 16. Jahrhundert, so als Spynell um 1528 in England, als Spinella 1546 durch Georgius Agricola oder als Spinellus durch Anselmus de Boodt (1609). Zur Wortherkunft gibt es unterschiedliche Deutungen. Einerseits wird Spinell auf das altgriechische Wort σπίν(ν)ος [spín(n)os] für „Funke“ bzw. „funkeln“ zurückgeführt, andererseits auf das lateinische Wort spina, spinus oder spinula für „Dorn“ oder „Zapfen“, womit auf die scharfkantige, oktaedrische Kristallform angespielt wird.[7]
Die Spinellstruktur gehört zu den ersten Kristallstrukturen, an denen eine erfolgreiche Röntgenstrukturanalyse ausgeführt wurde, kurz nachdem 1912 die Röntgenbeugung entdeckt worden war. Die Spinellstruktur wurde 1915 durch Shoji Nishikawa (1884–1952) anhand von Laue-Diagrammen aufgeklärt,[8] und unabhängig davon durch William Henry Bragg.[9][10]
Kristallstruktur
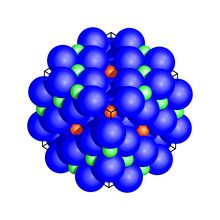
Blau: Anion (O2-)
Grün: Kation in Oktaederlücke (Al3+)
Orange: Kation in Tetraederlücke (Mg2+)
Die Kristallstruktur der Spinelle ist die verbreitetste Struktur von Verbindungen des Typs AB2X4 und eine der wichtigsten Strukturtypen in der technischen Mineralogie. Nach dem Hauptmineral der Spinellgruppe wird dieser Strukturtyp Spinellstruktur genannt, die Strukturberichte führen ihn unter der Bezeichnung H11 und das Pearson-Symbol ist cF56.
Spinelle kristallisieren meist mit kubischer Symmetrie der Raumgruppe Fd3m (Raumgruppen-Nr. 227). Eine Erniedrigung der Symmetrie z. B. auf tetragonal ist möglich, wie z. B. beim Hausmannit oder Deltalumit.
Die Anionen liegen auf der allgemeinen Punktlage 32e (uuu) mit der Punktsymmetrie 3m. Jedes Anion ist von vier Kationen umgeben, einem in einer Tetraederlücke und drei in Oktaederlücken. Die Anionen bilden ein kubisch flächenzentriertes Gitter (fcc). Die meist leicht verzerrte, kubisch dichteste Kugelpackung hat 64 Tetraederlücken, von denen 1/8 besetzt sind, und 32 Oktaederlücken, die zur Hälfte besetzt sind. Der freie Lageparameter u der Punktlage erlaubt eine leichte Verschiebung der Anionen parallel zur Diagonalen der Elementarzelle, der 3-zähligen Achse [111], und liegt bei natürlichen Spinellen zwischen 0,23 und 0,27. Ein Wert von 0,25 entspricht einer idealen kubisch dichtesten Kugelpackung mit unverzerrten Tetraeder- und Oktaederlücken. Werte kleiner als 0,25 führen zu gestauchten Oktaederpositionen und u > 0,25 zu gestreckten Oktaederlücken. Auch die Größe der Kationenpositionen variiert mit der Anionenposition. Eine Erhöhung von u führt zu einer Vergrößerung der Tetraederlücken und einer Verkleinerung der Oktaederlücken. Bei einem Wert von u = 0,2625 sind die mittleren Bindungslängen in Tetraeder- und Oktaederlücken gleich groß, sie nehmen also gleich große Kationen auf. Diese Variabilität von Größe und Verzerrung der Kationenpositionen ermöglicht die große Vielfalt der chemischen Zusammensetzungen der Verbindungen mit Spinellstruktur.[1]
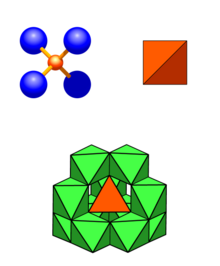
Oben links: Kation (orange) umgeben von 4 Anionen (blau) in tetraedrischer Koordination
Oben rechts: Koordinationspolyeder
Unten: Umgebung der Tetraederposition: 12 Oktaeder (über Ecken verknüpft)
Die Tetraederlücken liegen auf der festgelegten Punktlage 8a (1/8 1/8 1/8) mit der Punktsymmetrie -43m. Jedes Kation in einer Tetraederlücke ist von vier Anionen umgeben, die die Ecken eines Tetraeders bilden, in dessen Zentrum sich das Kation befindet. Über alle vier Ecken sind diese Tetraeder mit benachbarten Oktaedern verknüpft.[1][11]
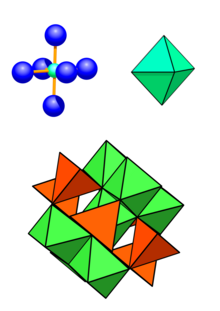
Oben links: Kation (grün) umgeben von 6 Anionen (blau) in oktaedrischer Koordination
Oben rechts: Koordinationspolyeder
Unten: Umgebung der Oktaederposition: 6 Oktaeder (über Kanten verknüpft) und 6 Tetraeder (über Ecken verknüpft)
Die Oktaederlücken liegen auf der speziellen Punktlage 16d (1/2 1/2 1/2) mit der Punktsymmetrie -3m. Die Kationen in den Oktaederlücken sind von sechs Anionen umgeben, die die Ecken eines Oktaeders bilden, in dessen Zentrum das Kation sitzt. Jeder dieser Oktaeder ist über gemeinsame Kanten mit sechs benachbarten Oktaedern verknüpft und über Ecken mit sechs benachbarten Tetraedern. Die Oktaeder bilden ein Gerüst aus kantenverknüpften Oktaedern, in dessen Hohlräumen die tetraedrisch koordinierten Kationen eingebettet sind.[1][11]
Welche Kationen welche Positionen besetzen, hängt im Wesentlichen von den Größen der Ionen ab, ihrer Ladung, der Geometrie ihrer Atomorbitale und der Ligandenfeldstabilisierungsenergie von Übergangsmetallionen in den unterschiedlichen Anionenumgebungen. So hat Zn2+ wegen seiner Elektronenkonfiguration (sp3-Hybridorbitale) eine starke Präferenz für die Tetraederposition, Mg2+ wegen seiner Größe ebenso, während z. B. Ti4+ wegen seiner Größe und Ladung die oktaedrische Umgebung bevorzugt, ebenso wie Mn3+ und Cr3+, die wegen ihrer Ligandenfeldstabilisierungsenergie eher auf Oktaederpositionen eingebaut werden.[3]
Spinelle, deren Tetraederposition von den A-Kationen besetzt ist (z. B. Mg, Zn), werden als normale Spinelle bezeichnet. Ist die Tetraederposition von den B-Kationen besetzt und die Oktaederposition zur Hälfte jeweils von A- und B-Kationen, spricht man von inversen Spinellen. Zwischen diesen beiden geordneten Verteilungen sind alle Zwischenstufen möglich. Beschreiben lässt sich dies mit der Formel
- (A1-iBi)[4](B2-iAi)[6],
worin in eckigen Klammern die Koordinationszahl der Position angegeben ist und i der Inversionsgrad des Spinells ist – 0 für normale Spinelle und 1 für inverse Spinelle. Vollständig ungeordnete Spinelle mit einer statistischen Verteilung von A- und B-Kationen auf die verschiedenen Positionen haben einen Inversionsgrad von 2/3.[1]
Minerale und Varietäten
Aus der Spinell-Supergruppe sind über 200 Verbindungen bekannt,[3] von denen 61 natürlich vorkommen (Stand 2023).[12] Sie enthalten 36 verschiedene Kationen unterschiedlichster Ladung:[1]
- 0: ☐ (Leerstelle)
- 1+: Ag+, Cu+, Li+, Na+
- 2+: Cd2+, Co2+, Cu2+, Fe2+, Hg2+, Mg2+, Mn2+, Ni2+, V2+, Zn2+
- 3+: Al3+, Co3+, Cr3+, Fe3+, Ga3+, In3+, Ir3+, Mn3+, Ni3+, Rh3+, Sc3+, V3+
- 4+: Ge4+, Mn4+, Si4+, Sn4+, Ti4+, V4+
- 5+: Sb5+
- 6+: Mo6+, W6+
Die Anionen können ein bis dreiwertig sein:[11]
- 1-: F-, Cl-, (CN)-
- 2-: O2-, S2-, Te2-, Se2-
- 3-: N3-
Bislang (2023) sind natürliche Spinelle nur mit den zweiwertigen Anionen O2-, S2-, Se2- bekannt. Die aktuelle Klassifikation der International Mineralogical Association (IMA) teilt die Spinelle nach diesen Anionen in drei Gruppen ein. Diese werden nach dem Verteilungsmuster der Kationenladungen in Untergruppen gegliedert.[11]
- 0-4: A0B4+2X4, z. B. ☐Mn4+2O4
- 1-3,5: A+B3+B4+X4, z. B. Cu+Cr3+Cr4+S4
- 2-3: A2+B3+2X4, z. B. Mg2+Al3+2O4
- 4-2: A4+B2+2X4, z. B. Ti4+Mg2+2O4
- 6-1: A6+B+2X4, z. B. Mo6+Na+2O4
Die hier wiedergegebene IMA-Klassifikation beschränkt sich auf Minerale und führt die vielen nur synthetisch bekannten Spinelle nicht auf. Für die Definition, Benennung und Klassifizierung von Mineralen sind Ordnungs-Unordnungs-Phänomene wie der Invasionsgrad der Spinelle nicht von Belang.[13] Daher wird die Zusammensetzung der einzelnen Minerale hier immer als geordneter, normaler Spinell angegeben, auch für inverse Spinelle.[11]
| Spinell-Untergruppe (2-3) | A2+ | B3+2 | O2-4 | Oxispinelle mit im Mittel 2-wertigen A-Kationen und 3-wertigen B-Kationen |
|---|---|---|---|---|
| Spinell | Mg2+ | Al3+2 | O2-4 | |
| Dellagiustait | V2+ | Al3+2 | O2-4 | |
| Galaxit | Mn2+ | Al3+2 | O2-4 | |
| Hercynit | Fe2+ | Al3+2 | O2-4 | |
| Chihmingit | Ni2+ | Al3+2 | O2-4 | |
| Thermaerogenit | Cu2+ | Al3+2 | O2-4 | |
| Gahnit | Zn2+ | Al3+2 | O2-4 | |
| Magnesiocoulsonit | Mg2+ | V3+2 | O2-4 | |
| Vuorelainenit | Mn2+ | V3+2 | O2-4 | |
| Coulsonit | Fe2+ | V3+2 | O2-4 | |
| Magnesiochromit | Mg2+ | Cr3+2 | O2-4 | |
| Manganochromit | Mn2+ | Cr3+2 | O2-4 | |
| Chromit | Fe2+ | Cr3+2 | O2-4 | |
| Cochromit | Co2+ | Cr3+2 | O2-4 | |
| Nichromit | Ni2+ | Cr3+2 | O2-4 | 1978 von De Waal beschrieben, aber nicht durch die CNMNC der IMA anerkannt[14] |
| Zincochromit | Zn2+ | Cr3+2 | O2-4 | |
| Hausmannit | Mn2+ | Mn3+2 | O2-4 | |
| Hetaerolith | Zn2+ | Mn3+2 | O2-4 | |
| Magnesioferrit | Mg2+ | Fe3+2 | O2-4 | |
| Jakobsit | Mn2+ | Fe3+2 | O2-4 | |
| Magnetit | Fe2+ | Fe3+2 | O2-4 | |
| Trevorit | Ni2+ | Fe3+2 | O2-4 | |
| Cuprospinell | Cu2+ | Fe3+2 | O2-4 | |
| Franklinit | Zn2+ | Fe3+2 | O2-4 | |
| Guit | Co2+ | Co3+2 | O2-4 | |
| (A3+0,5A+0,5) | B3+2 | O2-4 | ||
| Chukochenit | (Al3+0,5Li+0,5) | Al3+2 | O2-4 | |
| (A3+0,66☐0,33) | B3+2 | O2-4 | Symmetrie-Erniedrigung von kubisch auf tetragonal bei Ordnung der Kationen und Leerstellen auf der Tetraederposition[11] | |
| Deltalumit | (Al3+0,66☐0,33) | Al3+2 | O2-4 | |
| Maghemit | (Fe3+0,66☐0,33) | Fe3+2 | O2-4 | Neu definiert durch Bosi et al. 2019[11] |
| (A4+0,5☐0,5) | B3+2 | O2-4 | Anmerkung | |
| Titanomaghemit | (Ti4+0,5☐0,5) | Fe3+2 | O2-4 | Neu definiert durch Bosi et al. 2019[11] |
| Ulvospinell-Untergruppe (4-2) | A4+ | B2+2 | O2-4 | Anmerkung |
| Ringwoodit | Si4+ | Mg2+2 | O2-4 | |
| Qandilit | Ti4+ | Mg2+2 | O2-4 | |
| Ahrensit | Si4+ | Fe2+2 | O2-4 | |
| Ulvöspinell | Ti4+ | Fe2+2 | O2-4 | |
| Brunogeierit | Ge4+ | Fe2+2 | O2-4 | |
| (A3+0,5A5+0,5) | B3+2 | O2-4 | Anmerkung | |
| Tegengrenit | (Mn3+0,5Sb5+0,5) | Mg2+2 | O2-4 | Neu definiert durch Bosi et al. 2019[11] |
| Filipstadit | (Fe3+0,5Sb5+0,5) | Mn2+2 | O2-4 | Neu definiert durch Bosi et al. 2019[11] |
| Carrollit-Untergruppe (1-3,5) | A+ | (B3+B4+) | S2-4 | Thiospinelle mit 1-wertigen A-Kation und im Mittel 3,5-wertigen B-Kationen |
|---|---|---|---|---|
| Cuprokalininit | Cu+ | (Cr3+Cr4+) | S2-4 | |
| Carrollit | Cu+ | (Co3+Co4+) | S2-4 | Die formale Ladung von Co in den Cu-haltigen Thiospinellen ist umstritten und beruht auf der Annahme von vollen 2 negativen Ladungen des Schwefelanions.[11] |
| Fletcherit | Cu+ | (Ni3+Ni4+) | S2-4 | Die formale Ladung von Ni in den Cu-haltigen Thiospinellen ist umstritten und beruht auf der Annahme von vollen 2 negativen Ladungen des Schwefelanions.[11] |
| Cuproiridsit | Cu+ | (Ir3+Ir4+) | S2-4 | |
| Ezochiit | Cu+ | (Rh3+Pt4+) | S2-4 | |
| Malanit | Cu+ | (Ir3+Pt4+) | S2-4 | Neu definiert durch Bosi et al. 2019[11] |
| A+ | (B3+1,5B5+0,5) | S2-4 | ||
| Florensovit | Cu+ | (Cr3+1,5Sb5+0,5) | S2-4 | |
| A+ | (B2+0,5B4+1,5) | S2-4 | ||
| Rhodostannit | Cu+ | (Fe2+0,5Sn4+1,5) | S2-4 | Neu definiert durch Bosi et al. 2019[11] |
| Toyohait | Ag+ | (Fe2+0,5Sn4+1,5) | S2-4 | Neu definiert durch Bosi et al. 2019[11] |
| Linneit-Untergruppe (2-3) | A2+ | B3+2 | S2-4 | Thiospinelle mit im Mittel zweiwertigen A-Kation und dreiwertigen B-Kationen |
| Joegoldsteinit | Mn2+ | Cr3+2 | S2-4 | |
| Daubréelith | Fe2+ | Cr3+2 | S2-4 | |
| Kalininit | Zn2+ | Cr3+2 | S2-4 | |
| Greigit | Fe2+ | Fe3+2 | S2-4 | |
| Linneit | Co2+ | Co3+2 | S2-4 | |
| Grimmit | Ni2+ | Co3+2 | S2-4 | |
| Violarit | Fe2+ | Ni3+2 | S2-4 | |
| Siegenit | Co2+ | Ni3+2 | S2-4 | |
| Polydymit | Ni2+ | Ni3+2 | S2-4 | |
| Indit | Fe2+ | In3+2 | S2-4 | |
| Cadmoindit | Cd2+ | In3+2 | S2-4 | |
| Xingzhongit | Pb2+ | Ir3+2 | S2-4 | Neu definiert durch Bosi et al. 2019[11] |
| (A+0,5A3+0,5) | B3+2 | S2-4 | ||
| Cuprorhodsit | (Cu+0,5Fe3+0,5) | Rh3+2 | S2-4 | Neu definiert durch Bosi et al. 2019[11] |
| Tyrrellit-Untergruppe (1-3,5) | A+ | (B3+B4+) | Se2-4 | Selenospinelle mit 1-wertigen A-Kation und im Mittel 3,5-wertigen B-Kationen |
|---|---|---|---|---|
| Tyrrellit | Cu+ | (Co,Ni)3,5+2 | Se2-4 | Die formale Ladung von Co und Ni in den Cu-haltigen Selenospinellen ist umstritten und beruht auf der Annahme von vollen 2 negativen Ladungen des Selenanions.[11] |
| Nickeltyrrellit | Cu+ | Ni3,5+2 | Se2-4 | |
| Bornhardtit-Untergruppe (2-3) | A2+ | B3+2 | Se2-4 | Selenospinelle mit 2-wertigen A-Kation und 3-wertigen B-Kationen |
| Bornhardtit | Co2+ | Co3+2 | Se2-4 | |
| Trüstedtit | Ni2+ | Ni3+2 | Se2-4 |
Vorkommen
Spinelle sind geologisch außerordentlich wichtig.[14] Viele Minerale kristallisieren in der Spinellstruktur, darunter sind neben den Oxiden auch Sulfide, Selenide und Silikate. Die aktuelle und von der IMA/CNMNC neu definierte Spinell-Supergruppe führt derzeit 56 Minerale (Stand 2018).[11] Es wird vermutet, dass der Spinell Ringwoodit einen größeren Anteil des Erdmantels bildet.[14]
Verwendung
Der Cobalt-Spinell CoAl2O4 Cobaltaluminat (Thénards Blau) ist als Farbpigment in der Industrie und in der klassischen analytischen Chemie als Nachweisreagenz bekannt. Auch andere Spinelle werden als gegenüber Licht, Wetter und Chemikalien beständige Pigmente verwendet.[15]. Ferner werden farbige oder schwarze Spinelle als Schmucksteine verwendet, insbesondere die des eigentlichen Spinells. Eisenspinelle werden als Fotokatalysatoren eingesetzt, Cobaltchromit als Katalysator beim Abbau von Schadstoffen.[16]
Magnetit ist eines der wichtigsten Eisenerze. Es dient als Pigment und wurde in der magnetischen Datenspeicherung eingesetzt. Ähnlich wie Yttrium-Eisen-Granat werden Magnetit und verwandte Spinelle auch als Ferrite in Ferritkernen (auch für Mikrowellen geeignet) eingesetzt. Sie besitzen allerdings höhere Verluste.
Literatur
- Will Kleber, Joachim Bohm, Hans-Joachim Bautsch: Einführung in die Kristallographie. 18. Ausgabe. Oldenbourg Wissenschaftsverlag, 1998, ISBN 978-3-486-27319-9.
- Taschenbuch der Hochfrequenztechnik, Lange K. + Löcherer K.H., Springer-Verlag, ISBN 3-540-54715-0, S. L38 (Spinelle)
Einzelnachweise
- ↑ Hochspringen nach: a b
c d e
f Ferdinando Bosi: Chemical and structural variability in cubic spinel
oxides. In: Acta Crystallographica. B75, 2019,
S. 279–285,
doi:
 10.1016/j.physrep.2021.04.002 (englisch).
10.1016/j.physrep.2021.04.002 (englisch).
- ↑ Aristoteles: De anima. Band 1 (1), 350 v. Chr., S. 402a1.
- ↑ Hochspringen nach: a b
c Vladimir Tsurkan, Hans-Albrecht Krug von Nidda, Joachim Deisenhofer, Peter Lunkenheimer, and Alois Loidl:
On the complexity of spinels: Magnetic, electronic, and polar ground states. In:
Physics Reports. Band
962, 3. September 2021, S. 1–86,
doi:
 10.1016/j.physrep.2021.04.002 (englisch).
10.1016/j.physrep.2021.04.002 (englisch).
- ↑ Hochspringen nach: a b Li Shu-Hua:
Origine de la Boussole II. Aimant et Boussole. In: Isis. Band 45 (2), 1954,
doi:
 10.1086/348315 (französisch).
10.1086/348315 (französisch).
- ↑ Amelia Carolina Sparavigna: Magnetic Compasses and Chinese Architectures. In: arXiv History and Philosophy of Physics
(physics.hist-ph). 2017,
doi:
 10.48550/arXiv.1709.07056 (englisch).
10.48550/arXiv.1709.07056 (englisch).
- ↑ Huang Xing 黄兴: Experimental
Research on the South-Pointing Loadstone Spoon (Sinan). In: Chinese Annals of History of Science and
Technology. Band 3 (1), 2019,
S. 021–043,
doi:
 10.3724/SP.J.1461.2019.03021 (englisch).
10.3724/SP.J.1461.2019.03021 (englisch).
- ↑ Hans Lüschen: Die Namen der Steine. Das Mineralreich im Spiegel der Sprache. 2. Auflage. Ott Verlag, Thun 1979, ISBN 3-7225-6265-1, S. 323–324.
- ↑ Shoji Nishikawa: Structure of some crystals of the spinel group. In: Proceedings of the Tokyo Mathematico-Physical Society. Band 8, 1915, S. 199–209.
- ↑ William Henry Bragg: XXX. The structure
of the spinel group of crystals. In: Philosophical Magazine Series 6.
Band 30, Nr. 176, 1915,
S. 305–315,
doi:
 10.1080/14786440808635400 (englisch,
10.1080/14786440808635400 (englisch,
 zenodo.org [PDF;
511 kB] autom. Download).
zenodo.org [PDF;
511 kB] autom. Download).
- ↑ R. Gross, Übersetzung und Erläuterung von "W. H. Bragg: Structure of the spinel group of
crystals", in: Neues Jahrbuch für Mineralogie, Geologie and Paläontologie, 1. Band 1917
 online (Internet Archiv)
online (Internet Archiv)
- ↑ Hochspringen nach: a b
c d e
f g h
i j k
l m n
o p q
r s Ferdinando Bosi, Cristian Biagioni, Marco Pasero:
Nomenclature and classification of the spinel supergroup. In: European Journal of Mineralogy. Band 31,
Nr. 1, 12. September 2018,
S. 183–192,
doi:
 10.1127/ejm/2019/0031-2788 (englisch).
10.1127/ejm/2019/0031-2788 (englisch).
- ↑ Malcolm Back, William D. Birch, Michel Blondieau und andere: The New IMA List of Minerals – A Work in Progress – Updated: March 2019. (PDF) In: cnmnc.main.jp. IMA/CNMNC, Marco Pasero, März 2019 (englisch).
- ↑ Frank. C. Hawthorne: The
Use Of End-Member Charge-Arrangements In Defining New Mineral Species And Heterovalent Substitutions In Complex Minerals. In: The Canadian Mineralogist. Band 40, 2002,
S. 699–710 (englisch,
 researchgate.net
[PDF; 309 kB]).
researchgate.net
[PDF; 309 kB]).
- ↑ Hochspringen nach: a b
c Cristian Biagioni, Marco Pasero: The systematics of the spinel-type minerals: An overview.
In: American Mineralogist. Band 99,
Nr. 7, 2014,
S. 1254–1264,
doi:
 10.2138/am.2014.4816
(
10.2138/am.2014.4816
(  Vorabversion online
[PDF]).
Vorabversion online
[PDF]).
- ↑
 Kreidezeit Naturfarben GmbH – Pigmente,
Produktinformation (PDF 159 kB)
Kreidezeit Naturfarben GmbH – Pigmente,
Produktinformation (PDF 159 kB)
- ↑ Christian Suchomski: Strukturelle, optische und
magnetische Eigenschaften von Nanokristallinen Metalloxid-Dünnfilmen mit mesoporöser Morphologie. Inaugural-Dissertation zur Erlangung des akademischen Grades „Doctor rerum
naturalium“. Physikalisch-Chemisches Institut der Justus-Liebig-Universität Gießen, Gießen März 2012,
S. 7
(
 uni-giessen.de
[PDF; 11,4 MB] zur Verwendung siehe Seite 7, Kapitel 2.1 Chrom- und
Eisen-basierte Spinelle).
uni-giessen.de
[PDF; 11,4 MB] zur Verwendung siehe Seite 7, Kapitel 2.1 Chrom- und
Eisen-basierte Spinelle).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.02. 2025