Kubisches Kristallsystem

Würfelförmiger Pyrit, Navajún, La Rioja, Spanien

Sphaleritstufe (Größe: 2,3 × 2,3 × 1,2 cm) aus der Idarado Mine, Colorado, USA

Das kubische Kristallsystem gehört zu den sieben Kristallsystemen in der Kristallographie. Es umfasst alle Punktgruppen, die in vier unterschiedlichen Richtungen jeweils eine dreizählige Dreh- oder Drehinversionsachse besitzen. Diese vier dreizähligen Achsen verlaufen in kubischen Kristallen entlang der vier Raumdiagonalen der Elementarzellen, deren Gestalt einem Würfel entspricht. Oft werden auch (drei) vierzählige Drehachsen als Eigenschaft des kubischen Kristallsystems angegeben. Dies stimmt für das Achsensystem und die abstrakten kubischen Gitter, aber nicht allgemein für Kristallstrukturen, da es kubische Punktgruppen gibt, die keine vierzählige Symmetrie besitzen.

Punktgruppen

Das kubische Kristallsystem umfasst die Punktgruppen $\ 2 3, \, m \bar 3, \, 4 3 2,\, \bar 4 3 m$ und $m \bar 3 m$ . Sie bilden die kubische Kristallfamilie und können mit dem kubischen Gittersystem beschrieben werden.

Gittersystem

Das kubische Gittersystem hat die Holoedrie $m \bar 3 m$ . Es gibt nur eine Möglichkeit dafür, dass in einem Gitter unterschiedliche dreizählige Achsen existieren können: als Raumdiagonalen eines Würfels. Daher hat das kubische Gitter drei rechte Winkel und auch drei gleich lange Achsen. Es ergeben sich also folgende Bedingungen:

$a\ = b\ = c\$
$\alpha\ = \beta\ = \gamma\ = 90^\circ$

Die Aufstellung erfolgt im Allgemeinen gemäß dem in den International Tables for Crystallography vorgegebenen Standard. Das kubische Gittersystem wird mit c (en:cubic) abgekürzt.

Bravais-Gitter

Elementarzelle einer Kubisch primitiven Kristallstruktur

Elementarzelle einer kubisch raumzentrierten Kristallstruktur

Elementarzelle einer kubisch flächenzentrierten Kristallstruktur

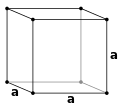Kubisch primitives Gitter: cP
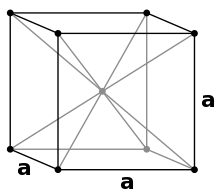Kubisch raumzentriertes Gitter: cI
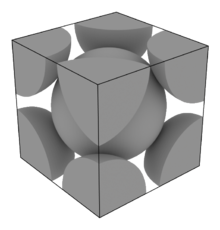
Kubisch flächenzentriertes Gitter: cF

Im Kubischen gibt es drei Bravais-Gitter, die in der Literatur auch oft mit ihrer englischen Abkürzung bezeichnet werden: das primitive (sc für simple cubic), das raumzentrierte oder innenzentrierte (krz bzw. bcc für body centered cubic) und das flächenzentrierte (fcc für face centered cubic) Gitter.

Anmerkungen zur Verwendung des Begriffs Gitter

Die Kristallstruktur wird durch ein Gitter und eine Basis beschrieben. Das Gitter (auch Raumgitter oder Translationsgitter genannt) ist die Menge aller Translationsvektoren, die einen Kristall in sich selbst überführen. Die Lage der Atome wird durch die Basis beschrieben. Kristallstrukturen, die nicht nur dasselbe Kristallgitter besitzen, sondern bei denen auch dieselben Lagen (allerdings mit unterschiedlichen Atomen) besetzt sind, bilden einen Strukturtyp. Außerhalb der Fachliteratur wird dieser Unterschied zwischen Gitter und Strukturtyp allerdings nicht immer beachtet. In dem Fall, dass es in der Elementarzelle nur ein Atom gibt, das auf der Lage (0,0,0) liegt, spricht man auch von einem kubisch primitiven (bzw. raumzentrierten oder flächenzentrierten) Gitter als Strukturtyp. Enthält die Basis mehrere Atome, spricht man auch von ineinandergestellten kubischen Gittern.

Während diese Begriffsverwendung noch vernünftig ist, so gibt es, insbesondere im Internet, auch Begriffe und damit verbundene Vorstellungen, die definitiv falsch sind.

Die Punkte, die zur Darstellung von Bravais-Gittern verwendet werden, stellen keine Atome dar. Es gibt Strukturtypen, bei denen im Ursprung des Gitters kein Atom liegt. (Der bekannteste Strukturtyp mit dieser Eigenschaft ist die hexagonal dichteste Kugelpackung (hcp))
Es gibt keine kubisch-primitiven (-raumzentrierten bzw. -flächenzentrierten) Kristallsysteme. Der Begriff der Zentrierung bezieht sich einzig und alleine auf ein Gitter.
Die Begriffe hcp (hexagonal closed packed) und ccp (cubic closed packed) stehen für Kugelpackungen. Diese entsprechen Strukturtypen. Die Angaben zu Koordinationszahlen und Packungsdichte beziehen sich auch nur auf diese Strukturtypen. Es sind aber keine Gitter. Insbesondere ist fcc nicht gleich ccp! Es gibt viele weitere Strukturen, die ein kubisch flächenzentriertes Gitter besitzen. Einzig richtig ist, dass die kubisch dichteste Kugelpackung mit einem kubisch flächenzentrierten Gitter beschrieben werden kann.

Darstellung durch primitive Gitter

Die zentrierten kubischen Gitter können auch durch primitive (allerdings nicht-kubische) Gitter beschrieben werden. Der Zusammenhang zwischen den primitiven und nicht-primitiven Gittervektoren wird in folgender Tabelle zusammengestellt. Dabei ist jeweils die Gitterkonstante und nicht zwangsläufig die Länge des Vektors ${\vec {a}}$ . Die Formel zur Berechnung findet man im Artikel zum Reziproken Gitter

Gittertyp	Gittervektoren des realen Gitters	Gittervektoren des reziproken Gitters
sc-Gitter	$\vec{a} = a \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} , \vec{b} = a \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} , \vec{c} = a \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$	$\vec{a'} = \frac{2 \pi}{a}\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} , \vec{b'} =\frac{2 \pi}{a}\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} , \vec{c'} = \frac{2 \pi}{a}\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$
bcc-Gitter	$\vec{a} = \frac{a}{2} \begin{pmatrix} -1 \\ 1 \\ 1 \end{pmatrix} , \vec{b} = \frac{a}{2} \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} , \vec{c} = \frac{a}{2} \begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}$	$\vec{a'} = \frac{2\pi}{a} \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} , \vec{b'} = \frac{2\pi}{a} \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} , \vec{c'} = \frac{2\pi}{a} \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$
fcc-Gitter	$\vec{a} = \frac{a}{2} \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} , \vec{b} =\frac{a}{2} \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} , \vec{c} = \frac{a}{2} \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$	$\vec{a'} =\frac{2\pi}{a} \begin{pmatrix} -1 \\ 1 \\ 1 \end{pmatrix} , \vec{b'} = \frac{2\pi}{a} \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} , \vec{c'} =\frac{ 2\pi}{a} \begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix}$

Das reziproke Gitter eines sc-Gitters ist also wieder ein sc-Gitter. Das reziproke Gitter eines fcc-Gitters ist ein bcc-Gitter und umgekehrt.

Punktgruppen im kubischen Kristallsystem und ihre physikalischen Eigenschaften

Zur Beschreibung der kubischen Kristallklassen in Hermann-Mauguin-Symbolik werden die Symmetrieoperationen bezüglich vorgegebener Richtungen (Blickrichtungen) im Gitter-System angegeben. Die Blickrichtung des 1. Symbols ist die a-Achse (<100>), des 2. Symbols die Raumdiagonale (<111>) und des 3. Symbols die Flächendiagonale (<110>).

Charakteristisch für die kubischen Raumgruppen ist eine 3 (3) an der 2. Stelle des Raumgruppensymbols.

Punktgruppe (Kristallklasse)								Physikalische Eigenschaften ^{[Anm. 1]}				Beispiele
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Internationales Symbol (Hermann-Mauguin)		Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Voll	Kurz	Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
28	kubisch	tetraedrisch-pentagondodekaedrisch	T	23	23	m3	195–199	+	+	–	+	Ullmannit Natriumbromat
29		disdodekaedrisch	T_h	2/m3	m3	m3	200–206	–	–	–	–	Pyrit Kalialaun
30		pentagon-ikositetraedrisch	O	432	432	m3m	207–214	+	+	–	–	Maghemit Ye’elimit
31		hexakistetraedrisch	T_d	43m	43m		215–220	–	–	–	+	Sphalerit Sodalith
32		hexakisoktaedrisch	O_h	4/m32/m	m3m		221–230	–	–	–	–	Diamant Kupfer
↑ Bei den Angaben zu den physikalischen Eigenschaften bedeutet „−“ aufgrund der Symmetrie verboten und „+“ erlaubt. Über die Größenordnung der optischen Aktivität, Pyro- und Piezoelektrizität sowie des SHG-Effekts kann rein aufgrund der Symmetrie keine Aussage getroffen werden. Man kann aber davon ausgehen, dass stets eine zumindest schwache Ausprägung der Eigenschaft vorhanden ist.

Literatur

D. Schwarzenbach: Kristallographie. Springer, Berlin u. a. 2001, ISBN 3-540-67114-5.
Walter Borchard-Ott: Kristallographie. Eine Einführung für Naturwissenschaftler. 7. überarbeitete und erweiterte Auflage. Springer, Berlin u. a. 2009, ISBN 978-3-540-78270-4.

Basierend auf einem Artikel in:

Wikipedia.de