Zerfallsgesetz

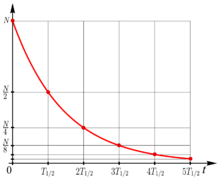
Exponentielle Abnahme einer Größe vom anfängliches Wert N – z.B. der Zahl radioaktiver Atomkerne in einer gegebenen Substanzprobe – mit der Zeit t.

Zerfallsgesetz ist die in der Physik übliche Bezeichnung der Gleichung, die eine exponentielle zeitliche Abnahme von Größen beschreibt. In der Kernphysik gibt das Zerfallsgesetz die Anzahl der zu einem Zeitpunkt noch nicht zerfallenen Atomkerne einer radioaktiven Substanzprobe an. Diese Anzahl beträgt

$N(t)=N_{0}\cdot {\mathrm e}^{{-\lambda t}}$ ,

wobei $N_{0}$ die Anzahl der am Anfang ( t=0 ) vorhandenen Atomkerne und $\lambda$ die Zerfallskonstante des betreffenden Nuklids ist.

Herleitung

Betrachtet man ein radioaktives Präparat mit anfänglich $N_{0}$ Atomkernen und der Aktivität , so gilt für die Anzahl der in der Zeit noch nicht zerfallenen Kerne:

${\begin{aligned}A&=-{\frac {\mathrm {d} N}{\mathrm {d} t}}\qquad {\text{mit }}A=\lambda \cdot N\\-\lambda \cdot N&={\frac {\mathrm {d} N}{\mathrm {d} t}}\\-\lambda \cdot \mathrm {d} t&={\frac {1}{N}}\cdot \mathrm {d} N\\\int _{0}^{t}-\lambda \cdot \mathrm {d} t'&=\int _{N_{0}}^{N}{\frac {1}{N'}}\cdot \mathrm {d} N'\\-\lambda t-(-\lambda \cdot 0)&=\ln(N)-\ln(N_{0})\\-\lambda t&=\ln \left({\frac {N}{N_{0}}}\right)\\\mathrm {e} ^{-\lambda t}&={\frac {N}{N_{0}}}\\N(t)&=N_{0}\cdot \mathrm {e} ^{-\lambda t}\end{aligned}}$

Nach der Zeit sind also von $N_{0}$ Ausgangskernen noch N(t) übrig.

Mittlere Lebensdauer

Die Zerfallskonstante $\lambda$ (Lambda) ist der Kehrwert der mittleren Lebensdauer $\tau =1/\lambda$ , also der Zeit, nach der die Zahl der Atome sich um den Faktor $\mathrm {e} =2{,}71828\dotso$ verringert hat. $\tau$ (Tau) unterscheidet sich von der Halbwertszeit $T_{1/2}$ nur um den konstanten Faktor $\ln 2$ :

$T_{1/2}={\frac {\ln 2}{\lambda }}=\tau \cdot \ln 2\approx 0{,}693\cdot \tau$

Damit ergibt sich für das Zerfallsgesetz auch folgende Form:

$N(t)=N_{0}\cdot e^{-{\frac {ln(2)}{T_{1/2}}}t}$

Basierend auf einem Artikel in:

Wikipedia.de