
Relativistisches Additionstheorem für Geschwindigkeiten
Das Relativistische Additionstheorem für Geschwindigkeiten besagt, wie
die Geschwindigkeit
eines Objekts in einem bestimmten Bezugssystem
zu bestimmen ist, wenn das Objekt sich mit einer Geschwindigkeit
gegenüber einem zweiten Bezugssystem bewegt, das sich selber gegenüber dem
ersten mit einer Geschwindigkeit
bewegt. Sie können aus der Lorentztransformation
für gegeneinander bewegte Inertialsysteme
hergeleitet werden.
In der klassischen
Mechanik werden Geschwindigkeiten vektoriell
addiert ()
und haben daher keine obere Schranke. Da aber nach der speziellen
Relativitätstheorie die Geschwindigkeit eines Objekts die Lichtgeschwindigkeit
nicht überschreiten kann, können die klassischen Gleichungen nur eine Näherung
sein. Unterschiede machen sich bemerkbar, wenn eine oder beide der zu
addierenden Geschwindigkeiten nicht mehr vernachlässigbar klein gegenüber der
Lichtgeschwindigkeit ist.
Das relativistische Additionstheorem für Geschwindigkeiten ist durch Messungen bestätigt worden.
Definition
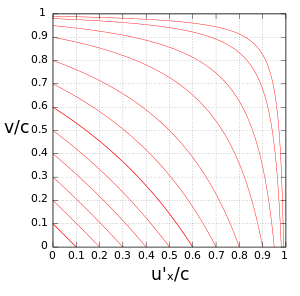
jeweils ausgedrückt in Bruchteilen der Lichtgeschwindigkeit
Die Konturlinien zeigen die resultierende Geschwindigkeit
(Abstufung geändert für
Je größer die beiden Ausgangsgeschwindigkeiten, desto stärker weicht das Ergebnis von der arithmetischen Addition ab:
auch von der resultierenden Geschwindigkeit kann die Lichtgeschwindigkeit nicht überschritten werden.
Ein Beobachter
bewege sich gegenüber dem Beobachter
mit der Geschwindigkeit
in Richtung der
-Achse.
Für den Beobachter
bewege sich ein Körper mit der Geschwindigkeit u'
Dann hat dieser Körper für den Beobachter
die Geschwindigkeit u mit den Komponenten
mit
- der Lichtgeschwindigkeit
und
- dem Lorentzfaktor (der stets größer gleich 1 ist)
Koordinatenfrei ausgedrückt: Die resultierende Geschwindigkeit
ergibt sich aus der einfachen Addition der Geschwindigkeiten (
)
mit folgenden Modifikationen:
- Die Geschwindigkeit
ist um den Faktor
kleiner.
- Die Komponenten der Geschwindigkeit
senkrecht zu
sind zusätzlich um den Faktor
kleiner.
Interpretation
Sind die beteiligten Geschwindigkeiten sehr klein gegenüber der Lichtgeschwindigkeit
so unterscheidet sich der Nenner (und auch der Term unter der Wurzel im Zähler) kaum von 1
und es ergibt sich in guter Näherung die übliche nichtrelativistische Geschwindigkeitsaddition:
Beispiel: in einem mit
fahrenden Zug
läuft eine Person mit
relativ zum Zug in Fahrtrichtung. Die von einem am Bahndamm stehenden Beobachter
gemessene Geschwindigkeit
der Person ist gerade mal um 0,17 nm/h langsamer als die bei
einfacher Addition erhaltenen
.
Zum Vergleich: der Durchmesser
eines Atoms liegt in der Größenordnung von 0,1 nm. Das heißt, der
„Zugläufer“ kommt in der Stunde knapp zwei Atomdurchmesser weniger weit,
als man es bei nichtrelativistischer Rechnung erwarten würde – was bei einer
zurückgelegten Strecke von 205 km sicher vernachlässigbar ist – ganz
abgesehen von dem von Laien häufig übersehenen Gesetz der gültigen
Ziffern.
Für Geschwindigkeiten nahe der Lichtgeschwindigkeit ergeben sich jedoch deutliche Abweichungen von der nichtrelativistischen Additionsregel, vgl. die folgenden Beispiele.
Folgerungen
Als Folge des Additionstheorems kann auch durch Überlagerung zweier Geschwindigkeiten die Lichtgeschwindigkeit nicht übertroffen werden.
1. Beispiel
Es seien
und
Dann ist
und nicht etwa 1,5c.
2. Beispiel
Ist die Geschwindigkeit u' für den Beobachter
gleich der Lichtgeschwindigkeit, dann ist sie es auch für den Beobachter
Sind zum Beispiel
Dann ergeben sich
Damit folgt
Herleitung
Um das Formelbild einfach zu halten, werden alle Geschwindigkeiten als
Vielfache der Lichtgeschwindigkeit in natürlichen
Einheiten angegeben. Dann haben Zeit und Länge dieselbe Maßeinheit und
die dimensionslose
Lichtgeschwindigkeit beträgt
Aus der inversen Lorentz-Transformation (Ersatz von
durch -
)
folgt für die Differentiale, da die Transformation linear ist,
Daher folgt für die Geschwindigkeiten, die der Beobachter
ermittelt,
Aufgelöst nach den gestrichenen Variablen ergeben sich folgende Beziehungen:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.03. 2021