Fortpflanzungskonstante

Die Fortpflanzungskonstante, manchmal auch Ausbreitungskonstante, Ausbreitungskoeffizient oder Ausbreitungsmaß genannt, ist eine Größe, welche die Ausbreitung einer Welle (z. B. einer elektromagnetischen Welle in der Leitungstheorie und der Elektrodynamik) beschreibt. Sie hängt von den Eigenschaften des Mediums ab, in dem sich die Welle ausbreitet.

Bei sinusförmigen Signalen und der Anwendung der komplexen Wechselstromrechnung ist sie eine komplexe Größe und kann in Real- und Imaginärteil zerlegt werden ( sei die imaginäre Einheit):

$\gamma =\alpha +j\beta$

Der Realteil der Fortpflanzungskonstante $\alpha$ heißt Dämpfungskonstante, der Imaginärteil $\beta$ Phasenkonstante. Sie bestimmen die Dämpfung bzw. die Phasendrehung der Welle und sind im Allgemeinen frequenzabhängig. Als alternative Beschreibungsgröße (besonders bei Funk- und Schallwellen) verwendet man oft die komplexe Wellenzahl :

$\gamma =jk$

Die Fortpflanzungskonstante in der Leitungstheorie

Wenn in der Theorie der Leitungen die allgemeine Lösung der Leitungsgleichung mit Hilfe einer Operatorenrechnung (z. B. der Laplace-Transformation) ermittelt wird, dann werden als sogenannte Wellenparameter neben dem Leitungswellenwiderstand auch die Fortpflanzungskonstante aus den Leitungsbelägen und der komplexen Frequenz definiert als

$\gamma ={\sqrt {(R'+sL')(G'+sC')}}$

Bei sinusförmigen Signalen kann man die komplexe durch die imaginäre Frequenz $j\omega$ ersetzen und erhält die spezielle Form

$\gamma = \sqrt{(R' + j\omega L')(G' + j\omega C')}$

Die Fortpflanzungskonstante beschreibt die Geschwindigkeit, Dämpfung und Verzerrung der über die Leitung laufenden Wellen, weil sie in die allgemeine Lösung der Leitungsgleichungen mit dem Faktor

$e^{{\pm \gamma x}}$

eingeht. Konkret werden diese drei Einflüsse durch die Ausbreitungsgeschwindigkeit

$v={\frac {1}{{\sqrt {L'C'}}}}$ ,

ein Dämpfungsmaß

$D={\frac {1}{2}}\cdot \left({\frac {R^{{\prime }}}{L^{{\prime }}}}+{\frac {G^{{\prime }}}{C^{{\prime }}}}\right)$

und ein Verzerrungsmaß

$V={\frac {1}{2}}\cdot \left({\frac {R^{{\prime }}}{L^{{\prime }}}}-{\frac {G^{{\prime }}}{C^{{\prime }}}}\right)$

(welches bei realen Leitungen immer positiv ist) bestimmt. Damit erhält man folgende gut interpretierbare Form der Ausbreitungskonstante

$\gamma ={\frac {1}{v}}\cdot {\sqrt {\left(s+D\right)^{{2}}-V^{{2}}}}$

welche wie im Folgenden zur Klassifizierung der Wellenausbreitung auf Leitungen benutzt werden kann.

Verlustlose Leitung

Bei einer verlustlosen Leitung sind aufgrund von R'=G'=0 sowohl als auch gleich 0. Dann reduziert sich die Ausbreitungskonstante auf

$\gamma ={\frac {s}{v}}$

und die Welle wird nur verzögert, aber nicht gedämpft oder verzerrt, denn der Ausdruck

$e^{{\pm s{\frac {x}{v}}}}$

stellt den Verschiebungsoperator der Laplace-Transformation dar.

Bei sinusförmigen Signalen wird die Ausbreitungskonstante rein imaginär. Die Verzögerung bedeutet dann eine linear mit der Frequenz zunehmende Phasendrehung.

$\gamma =j\beta ={\frac {j\omega }{v}}={\frac {2\pi j}{\lambda }}$

Dabei ist $\lambda$ die Wellenlänge der sich ausbreitenden sinusförmigen Welle.

Ortskurve der Fortpflanzungskonstante γ einer Leitung mit R' = 10 Ω/km, G' = 1 mS/km, L' = 2 mH/km und C' = 5 nF/km

Verzerrungsfreie Leitung

Bei einer verlustbehafteten, aber verzerrungsfreien Leitung (z. B. einem Krarupkabel) ist das Dämpfungsmaß D>0 , aber aufgrund der geltenden Heaviside-Bedingung ist das Verzerrungsmaß V=0 . Dann erscheint die Ausbreitungskonstante als

$\gamma ={\frac {s+D}{v}}$

und die Welle wird verzögert und gedämpft, aber nicht verzerrt:

$e^{{\pm (s+D){\frac {x}{v}}}}=e^{{\pm s{\frac {x}{v}}}}\cdot e^{{\pm D{\frac {x}{v}}}}$

Der linke Term stellt wieder die Verzögerung der Leitung dar, während der rechte Term eine Dämpfung der Welle repräsentiert, welche jedoch deren Form nicht verändert.

Bei sinusförmigen Signalen wird aus der Ausbreitungskonstante

$\gamma ={\frac {j\omega +D}{v}}={\frac {D}{v}}+{\frac {j\omega }{v}}=\alpha +j\beta$

Zur linear frequenzabhängigen Phasendrehung kommt jetzt eine frequenzunabhängige Dämpfung dazu:

$\alpha ={\frac {D}{v}}={\sqrt {R'\cdot G'}}$

erzerrungsbehaftete Leitung

Im allgemeinen Fall gilt die Heaviside-Bedingung jedoch nicht. Dann tritt ein dritter Faktor auf, der eine Formverzerrung (Dispersion) der über die Leitung laufenden Welle bewirkt. Seine allgemeine Auswertung ist praktisch nur mit numerischen Hilfsmitteln möglich.

Beim Spezialfall sinusförmiger Signale lässt sich dagegen eine explizite Zerlegung der Ausbreitungskonstante in Real- und Imaginärteil angeben:

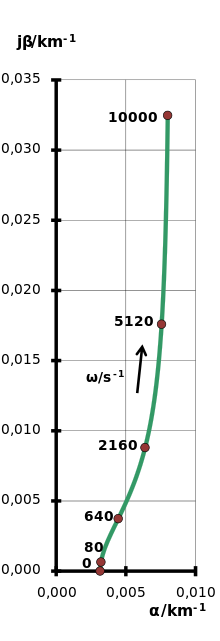
$\alpha ={\sqrt {{\frac {1}{2}}\cdot {\sqrt {\left(R'^{2}+\omega ^{2}L'^{2}\right)\left(G'^{2}+\omega ^{2}C'^{2}\right)}}+{\frac {1}{2}}\cdot \left(R'G'-\omega ^{2}L'C'\right)}}$

$\beta ={\sqrt {{\frac {1}{2}}\cdot {\sqrt {\left(R'^{2}+\omega ^{2}L'^{2}\right)\left(G'^{2}+\omega ^{2}C'^{2}\right)}}-{\frac {1}{2}}\cdot \left(R'G'-\omega ^{2}L'C'\right)}}$

Beide Komponenten sind nichtlinear von der Frequenz abhängig. Übersichtlich erkennt man das Verhalten an der Ortskurve der Ausbreitungskonstanten. Für die Frequenz 0 nimmt die Dämpfungskonstante ihren Gleichstromwert $\alpha _{=}={\sqrt {R'\cdot G'}}$ an. Für sehr hohe Frequenzen stimmt das Verhalten der Ausbreitungskonstante mit der verzerrungsfreien Leitung überein. Theoretisch strebt die Dämpfungskonstante gegen den frequenzunabhängigen Wert $\alpha _{\infty }={\frac {1}{2}}\cdot \left(R'{\sqrt {{\frac {C'}{L'}}}}+G'{\sqrt {{\frac {L'}{C'}}}}\right)$ , praktisch wächst sie jedoch wegen des Skin-Effekts mit der Frequenz weiter an. Für den Übergangsbereich sowie für bestimmte Leitungstypen und Frequenzbereiche sind in der Literatur vereinfachte Näherungsformeln zu finden.

Aufgrund der nichtlinearen Frequenzabhängigkeit der Phasenkonstante $\beta$ muss zwischen Phasengeschwindigkeit und Gruppengeschwindigkeit der Wellenausbreitung unterschieden werden.

Literatur

Peter Vielhauer: Theorie der Übertragung auf elektrischen Leitungen. Verlag Technik, Berlin 1970.

Basierend auf einem Artikel in:

Wikipedia.de