Linsenschleiferformel

f = Brennweite

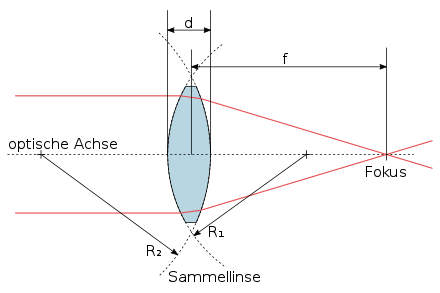
Die Linsenschleiferformel, auch Linsenmachergleichung, gibt an, wie die Brechkraft einer dünnen sphärischen Linse mit ihrer Form zusammenhängt. Dabei wird die Form der Linse durch die Radien der Kugeln beschrieben, die die Oberflächen der Linsen bilden. Weitere Größen, die Einfluss auf die Brechkraft haben, sind die Dicke der Linse, der Brechungsindex ihres Materials und der Brechungsindex des umgebenden Mediums.

Es seien

$R_{1},R_{2}$ die Kugelradien (hierbei ist zu beachten, dass die beiden Radien dann gleiche Vorzeichen haben, wenn die Mittelpunkte auf derselben Seite der Linse liegen [konvex-konkave Linse], jedoch unterschiedliche Vorzeichen, wenn die Linse bikonvex oder bikonkav ist; siehe hierzu auch: Sphärische Linsen),
die Dicke der Linse (gemessen in Höhe der optischen Achse),
$n_{0}$ der Brechungsindex des Mediums außerhalb der Linse,
der Brechungsindex des Linsenmaterials,
die Brennweite der Linse und
die Brechkraft.

Für optische Systeme mit gleichen Medien in Objektraum (1) und Bildraum (2) ( $n_{{1}}=n_{{2}}=n_{0}$ ) gilt allgemein:

$D={\frac {1}{f}}={\frac {n-n_{0}}{n_{0}}}\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-n_{0})d}{nR_{1}R_{2}}}\right)$

Ist unter gleichen Gegebenheiten das äußere Medium Luft $\Rightarrow n_{{1}}=n_{{2}}=n_{0}\approx 1$ gilt näherungsweise:

$D={\frac {1}{f}}=\left(n-1\right)\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2}}}\right)$

Bei dünnen Linsen, deren Dicke sehr viel kleiner als die Kugelradien ist, vereinfacht sich die Gleichung zur sogenannten Linsenschleiferformel:

$D={\frac {1}{f}}=\left(n-1\right)\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right)$

Basierend auf einem Artikel in:

Wikipedia.de