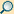Optische Abbildung
Die optische Abbildung ist in der Optik die Erzeugung eines Bildpunkts von einem Gegenstandspunkt durch Vereinigung von Licht, das vom Gegenstandspunkt ausgeht, mittels eines optischen Systems. Ein Bild ist die Gesamtheit aller einzelnen Bildpunkte, die alle Gegenstandspunkte repräsentieren.
Ein reelles Bild kann auf einem Schirm aufgefangen werden. Das Licht wird dort wirklich vereinigt. Ein virtuelles Bild scheint im Raum zu schweben. Mit strahlenoptischer Konstruktion vereinigt man dort auch Strahlen in Bildpunkten. Bei der Beobachtung scheint das Licht aus den virtuellen Bildpunkten zu kommen.
Das optische System kann aus Linsen, Spiegeln, Blenden o.Ä. bestehen. Nur die Punkte jeweils einer Objektebene werden in einer bestimmten Bildebene abgebildet. Je weiter die Gegenstandspunkte von dieser Objektebene entfernt sind, umso weniger scharf erscheinen sie in der Bildebene. Bei den meisten realen optischen Systemen ist die erträgliche Entfernung von der Objektebene – die Schärfentiefe – sehr klein.
Optische Systeme
Neben Linsen und Spiegeln erzeugen Blenden mit punktförmiger Öffnung optische Abbildungen. Sie lassen sich daher bereits alleine als optische Systeme – zum Beispiel als Lochkamera – zur Abbildung verwenden. Komplexere Systeme setzen sich aus mehreren optischen Bauelementen zusammen.
fotoObjektive bestehen zur Verkleinerung von Abbildungsfehlern oft aus mehreren Linsentypen verschiedener Glassorten, wirken jedoch insgesamt immer wie eine Sammellinse. Sammellinsen und Objektive liefern ein seitenverkehrtes, kopfstehendes Bild, zum Beispiel auf dem Film in einer Fotokamera.
Durch ein Umkehrprisma oder eine weitere abbildende Sammellinse kann das vom Objektiv erzeugte Bild sogleich nochmals gedreht werden, um das Zwischenbild z.B. im Sucher der Kamera oder zur Projektion im Vergrößerungsgerät oder Diaprojektor seitenrichtig und aufrecht abzubilden. Der Abstand von zwei Linsen entspricht dabei in etwa der Summe ihrer Brennweiten. Er muss erhöht werden, wenn ein naher Gegenstand betrachtet werden soll.
Das Prinzip eines astronomischen Fernrohrs besteht darin, das vom Objektiv erzeugte Bild mit einer Lupe bzw. einem Okular zu betrachten. Diese Lupe bzw. das Okular erzeugen erst zusammen mit der Augenlinse ein Bild auf der Netzhaut. Daher stehen die Bilder eines astronomischen Fernrohres und auch diejenigen eines Mikroskops, das ebenso funktioniert, auf dem Kopf. Feldstecher und viele Stereomikroskope haben daher oft Umkehrprismen, die häufig zugleich auch der Verkürzung der Baulänge dienen.
Die optische Abbildung mit Einzellinsen und sphärischen Spiegeln
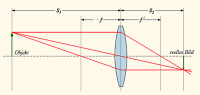
Die idealisierende Strahlenoptik geht dabei meist von einer unendlich weit entfernten punktförmigen Lichtquelle aus. Die von dort kommenden Strahlen verlaufen parallel zueinander. Befindet sich das abgebildete Objekt nicht im Unendlichen, sondern in der Entfernung einer endlichen Gegenstandsweite, so wird das Bild in der zugeordneten Bildweite erzeugt, die bei der Sammellinse stets größer ist als die Brennweite. Die Bildebene ist dabei gekrümmt.
Die weiteren Betrachtungen gelten für einen so genannten paraxialen Strahlengang. Alle Überlegungen gelten streng genommen nur für ein sehr schmales Gebiet um die optische Achse. Man idealisiert die Linsen zu unendlich dünnen Ebenen und vernachlässigt die Farbe des Lichts. Diese Vereinfachung ist bedeutsam, weil die Brennweite für jede Farbe anders ist.
Für Spiegel gelten die gleichen Gesetzmäßigkeiten wie für Linsen. Beim Betrachten der bildlichen Darstellungen muss man sich nur bewusst sein, dass an jeder Spiegelfläche eigentlich eine Richtungsumkehr der Strahlen erfolgen müsste.
Eine Sammellinse fokussiert parallel zur optischen Achse einfallende
Lichtstrahlen in den Brennpunkt, der den Abstand ,
die Brennweite, von der Linse
hat; umgekehrt wird von dem Brennpunkt ausgehendes Licht, das durch die Linse
fällt, in ein Bündel paralleler Lichtstrahlen umgelenkt.
Allgemein kann man Objekte mit Hilfe einer Sammellinse abbilden. Dabei
bezeichnet
den Abstand des Objektes von der Linse (auch Gegenstandsweite genannt), und
den Abstand des Bildes von der Linse (Bildweite). Wenn die Linse dünn ist, gilt
die Linsengleichung
.
Diese Sprechweise drückt aus, dass ein Objekt, das sich im Abstand
von einer Linse der Brennweite
befindet, auf einen Schirm abgebildet wird, der sich im Abstand
auf der anderen Seite der Linse befindet. Voraussetzung ist, dass
ist. Ein Fotoapparat arbeitet nach
diesem Prinzip; der Schirm ist in diesem Falle der zu belichtende Film (oder, in
digitalen Fotoapparaten, die zu belichtende Halbleiterschicht), auf den das so
genannte reelle Bild abgebildet wird.
Wenn sich jedoch das Objekt zwischen Brennpunkt und Linse befindet
(d.h. ),
dann wird
negativ; das Bild ist dann virtuell und erscheint vor der Linse. Obwohl
man ein virtuelles Bild nicht auf einen Schirm abbilden kann, ist es für einen
Beobachter, der durch die Linse blickt, ohne weitere Hilfsmittel sichtbar. Eine
Lupe arbeitet nach
diesem Prinzip.
Die Vergrößerung einer Linse ist durch
gegeben, wobei
der Vergrößerungsfaktor ist. Ein negatives
bedeutet hier ein reelles und auf dem Kopf stehendes Bild; ein positives
bedeutet ein virtuelles Bild, das aufrecht steht.
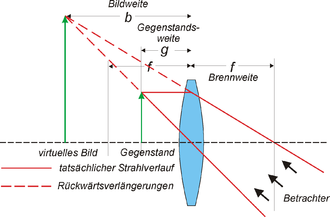
Obige Formel kann auch für Zerstreuungslinsen verwendet werden. Solche Linsen ergeben aber in allen Fällen virtuelle Bilder.
Die Berechnung (Modellierung) realer optischer Systeme aus einer Vielzahl von Linsen oder Spiegeln ist natürlich unvergleichlich aufwendiger, erfolgt aber analog der Verfahrensweise bei einzelnen Linsen.
Abbildungsfehler
Von Abbildungsfehlern spricht man dann, wenn die verschiedenen Lichtstrahlen, die von dem Objektpunkt ausgehen, nicht alle in einem Bildpunkt fokussiert werden.
Die wichtigsten Abbildungsfehler sind die sphärische und die chromatische Aberration.
Sphärische und chromatische Abbildungsfehler werden durch Systeme aus mehreren Linsen verschiedener Glassorten, sphärische Abbildungsfehler durch asphärische Linsen oder Gradientenlinsen korrigiert.
Spiegeloptiken weisen keine chromatische Aberration auf. Die sphärische Aberration eines sphärischen Spiegels kann durch eine Korrektur-Glasplatte behoben werden, die Bernhard Schmidt erfunden hat. Das von ihm entwickelte sogenannte Schmidt-Teleskop (auch Schmidt-Spiegel) hat daher ein besonders großes Blickfeld.
Eine Glasplatte (Planplatte) erzeugt einen Bildebenenversatz bzw. eine Unschärfe, die mit größer werdendem Öffnungswinkel zunimmt.
Der optischen Abbildung ähnliche Verfahren
Quasioptische Abbildungen
Allgemein kann man auch mit anderen Strahlungsarten (Mikrowellen, Röntgenstrahlung, Millimeterwellen, Terahertzstrahlung, Ultraviolett, Infrarotstrahlung) eine quasi-optische Abbildung erzielen, wenn es gelingt, durch Brechung oder Reflexion an gekrümmten Flächen ein Abbild zu erzeugen (z.B. Röntgenteleskop, Radioteleskop).
Bei der Elektronenoptik handelt es sich um fokussierende Strahlablenkung von Elektronen mittels magnetischer oder elektrischer Felder. Analog zu optischen Linsen gibt es dementsprechend aus Feldern bestehende Elektronenlinsen, diese weisen jedoch starke Abbildungsfehler auf. Man findet sie als abbildende Linsen in Bildverstärkern und Transmissions-Elektronenmikroskopen, aber auch zur Fokussierung in Kathodenstrahlröhren und Elektronenkanonen.
Abschattung
Ebenfalls keine optische Abbildung im eigentlichen Sinne stellt der Schattenwurf dar. Hier wird ein scharfes Bild dadurch gewährleistet, dass von einem Gegenstandspunkt praktisch nur ein Strahl ausgeht, so dass kein optisches System zur Vereinigung des Lichtes benötigt wird. Dies kann durch eine definierte Lichtquelle geschehen (punktförmig oder mit parallelem Licht). Der Gegenstand befindet sich im Strahlengang und absorbiert einen Teil des Lichtes. Im Gegensatz zur Abbildung ist grundsätzlich jede Ebene hinter dem Gegenstand als Projektionsebene geeignet. Dies wird z.B. bei der Röntgendiagnostik genutzt. Eine andere Möglichkeit ist das direkte Aufliegen des Gegenstandes auf der Projektionsebene, z.B. bei Kontaktkopien.
Geschichte
Einfache Formen der optischen Abbildung finden sich bereits in der freien Natur: So nehmen Lichtflecken, die unter einem löchrigen Blätterdach am Boden sichtbar sind, nicht die Form der Löcher, sondern die der Lichtquelle an. Das heißt, bei Sonnenschein sind sie rund (außer bei partiellen Sonnenfinsternissen, bei Mondschein nehmen sie die Form der Mondsichel an.)
Diese Beobachtung führt in einer ersten Abstraktion zur Entwicklung der Camera Obscura: In einem abgedunkelten Raum, dessen eine Wand ein kleines Loch hat, wird auf der Rückseite eine Abbildung der äußeren Realität erzeugt. Dieses altbekannte Phänomen findet seinen Niederschlag auch im Höhlengleichnis der Philosophie.
Das Bild, das in der Camera Obscura erzeugt wird, ist umso heller, je größer das Loch ist. Allerdings nimmt mit zunehmender Größe des Lochs auch die Schärfe des Bildes ab. Dieses Dilemma lässt sich durch Bündelung des Lichts mittels einer Sammellinse auflösen. Jede Sammellinse hat einen Fokus (Brennpunkt), der dadurch definiert ist, dass in ihm das Licht einer gedachten, unendlich weit entfernten, punktförmigen Lichtquelle wieder zu einem Punkt vereinigt wird. Ausgedehnte Objekte führen zu einem zweidimensionalen Bild in der durch den Fokuspunkt definierten Brennebene. Dies kann leicht mit einer Lupe und dem Licht einer strukturierten Lichtquelle (Glühlampe, Tageslicht im Fensterkreuz) auf einem Blatt Papier nachvollzogen werden.
Siehe auch
Literatur
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 4., bearbeitete und erweiterte Auflage. Wiley-VCH, Weinheim 2003, ISBN 3-527-40372-8.
- Eugene Hecht: Optik. Addison-Wesley, Bonn u.a. 1989, ISBN 3-925118-86-1.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.02. 2025