Spurdreieck (Vektorrechnung)

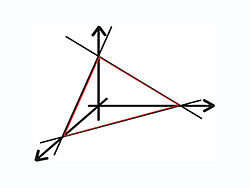
Spurdreieck in der Vektorgeometrie
(Skizze)

Als Spurdreieck einer Ebene im dreidimensionalen Raum bezeichnet man in der analytischen Geometrie dasjenige Dreieck, das von den Spurgeraden, also von den Schnittgeraden dieser Ebene mit den drei Koordinatenebenen begrenzt wird. Dabei ist die Schnittgerade zweier nicht komplanarer Ebenen als die Menge aller Punkte definiert, die zugleich in beiden Ebenen liegen. Die Ecken des Spurdreiecks liegen auf den Koordinatenachsen, sind also die Spurpunkte der betrachteten Ebene. Das Spurdreieck existiert nur dann, wenn die gegebene Ebene zu keiner der Koordinatenebenen parallel ist.

Bei Kenntnis des Spurdreiecks lässt sich sofort die Achsenabschnittsform der Ebenengleichung angeben. Sind $(a|0|0)$ , $(0|b|0)$ und $(0|0|c)$ die Ecken des Spurdreiecks (mit $a\neq 0$ , $b \ne 0$ , $c\neq 0$ ), so lautet die Achsenabschnittsform

${\frac {x}{a}}+{\frac {y}{b}}+{\frac {z}{c}}=1$ .

Für die Bestimmung der Achsenabschnitte und damit des Spurdreiecks aus einer in Normalenform oder Parameterform (Ortsvektor und zwei Richtungsvektoren) gegebenen Ebene gibt es einen rechnerischen und einen grafischen Lösungweg.

Basierend auf einem Artikel in:

Wikipedia.de