Cauchyscher Hauptwert

Als cauchyschen Hauptwert (nach Augustin-Louis Cauchy) bezeichnet man im mathematischen Teilgebiet der Analysis den Wert, den man einem divergenten Integral zuordnen kann, wenn sich divergente Teile verschiedenen Vorzeichens gegenseitig aufheben.

Definition

Der cauchysche Hauptwert ist ein Wert, den man gewissen divergenten Integralen zuordnen kann. Es gibt zwei unterschiedliche Fälle, in denen man von einem cauchyschen Hauptwert spricht.

Seien $-\infty \leq a<b\leq \infty$ und $c\in {]a,b[}$ eine reelle Zahl. Die Funktion $f\colon {]a,c[}\cup {]c,b[}\to \mathbb {R}$ sei Riemann-integrierbar. Existiert dann der Grenzwert

$\operatorname {CH}\int _{a}^{b}f(x)\,{\mathrm {d}}x:=\lim _{{\epsilon \rightarrow 0^{{+}}}}\left(\int _{a}^{{c-\epsilon }}f(x)\,{\mathrm d}x+\int _{{c+\epsilon }}^{b}f(x)\,{\mathrm d}x\right)\,,$

so nennt man $\operatorname {CH}\int _{a}^{b}f(x)\,{\mathrm d}x$ den cauchyschen Hauptwert.

Sei $f\colon \mathbb {R} \to \mathbb {R}$ eine stetige Funktion, dann heißt der Grenzwert, falls er existiert,

$\operatorname {CH}\int _{{-\infty }}^{\infty }f(x)\,{\mathrm d}x:=\lim _{{R\rightarrow \infty }}\int _{{-R}}^{R}f(x)\,{\mathrm d}x$

ebenfalls cauchyscher Hauptwert.

Es ist auch gebräuchlich, „V.P.“ (aus dem Franz. valeur principale) oder „P.V.“ (aus dem Engl. principal value) anstatt „CH“ zu schreiben.

Beziehung zwischen cauchyschem Hauptwert und uneigentlichem Integral

Existiert ein Integral über $\mathbb {R}$ im uneigentlichen Sinn, so existiert auch immer der cauchysche Hauptwert (nach der zweiten Definition) und diese beiden Werte stimmen überein. Aus der Existenz des cauchyschen Hauptwertes folgt hingegen noch nicht die Existenz des uneigentlichen Integrals.

Beispiel (CH 1/x)

cauchyscher Hauptwert – Beispiel

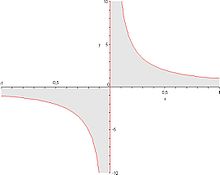
Es wird das bestimmte Integral $\textstyle \int _{{-1}}^{{1}}{\frac {1}{x}}\,{\mathrm d}x$ untersucht. Der Integrand ist für x=0 (ein innerer Punkt des Integrationsbereichs ]-1,1[ ) nicht definiert. Damit ist dieses Integral uneigentlich in $0$ . Die Stammfunktion des Integranden $\tfrac{1}{x}$ ist $\ln \left|x\right|$ .

${\begin{aligned}\Rightarrow \int _{-1}^{1}{\frac {1}{x}}\,\mathrm {d} x=&\int _{-1}^{0}{\frac {1}{x}}\,\mathrm {d} x+\int _{0}^{1}{\frac {1}{x}}\mathrm {d} x={\Big [}\ln \left|x\right|{\Big ]}_{x=-1}^{0}+{\Big [}\ln \left|x\right|{\Big ]}_{x=0}^{1}\\=&\lim _{x\rightarrow 0^{-}}\ln \left|x\right|-\ln \left|-1\right|+\ln \left|1\right|-\lim _{x\rightarrow 0^{+}}\ln \left|x\right|=-\infty -\left(-\infty \right)\end{aligned}}$

Dieses Integral existiert also nicht als uneigentliches Riemann-Integral, der cauchysche Hauptwert beträgt jedoch $0$ :

$\operatorname {CH}\int _{{-1}}^{{1}}{\frac {1}{x}}\,{\mathrm d}x=\lim _{{\epsilon \rightarrow 0^{{+}}}}\left(\int _{{-1}}^{{0-\epsilon }}{\frac {1}{x}}\,{\mathrm d}x+\int _{{0+\epsilon }}^{1}{\frac {1}{x}}\,{\mathrm d}x\right)=\lim _{{\epsilon \rightarrow 0^{{+}}}}(\ln(\epsilon )-\ln(\epsilon ))=0$

Der Cauchy-Hauptwert ermöglicht es also, einem Integral einen Wert zuzuordnen, das weder im riemannschen Sinn noch im lebesgueschen Sinn existiert.

Wenn auf der reellen Achse stetig und nur auf einem beschränkten Intervall von null verschieden ist, existiert also insbesondere der Ausdruck $\textstyle \operatorname {CH}\int _{{-\infty }}^{{+\infty }}f(x){\frac {1}{x}}\,{\mathrm d}x$ . Das heißt, dass $\operatorname {CH}{\tfrac {1}{x}}$ wie die Delta-Distribution auch als Distribution verstanden werden kann.

Substitution i. Allg. nicht erlaubt

Der Hauptwert eines Integrals bleibt jedoch im Allgemeinen nicht unter Substitution invariant. Wenn man etwa die Funktion $\varphi$ durch $\varphi (x)=x^{3}$ für $x\leq 0$ und $\varphi (x)=x^{2}$ für $x\geq 0$ definiert, so gilt zwar nach der Substitutionsregel

$\int _{{\varphi (a)}}^{{\varphi (b)}}{\frac 1t}\,{\mathrm d}t=\int _{a}^{b}{\frac {1}{\varphi (x)}}\varphi '(x)\,{\mathrm d}x$

wann immer $0<a\leq b$ oder $a\leq b<0$ gilt. Für a<0<b ist jedoch der Hauptwert des linken Integrals eine endliche Zahl, der Hauptwert des rechten Integrals ist aber $-\infty$ :

$\operatorname {CH}\int _{{a^{3}}}^{{b^{2}}}{\frac 1t}\,{\mathrm d}t=\ln {\biggl |}{\frac {b^{2}}{a^{3}}}{\biggr |}$

$\operatorname {CH}\int _{a}^{b}{\frac {\varphi '(x)}{\varphi (x)}}\,{\mathrm d}x=\lim _{{\varepsilon \to 0+}}{\biggl (}\int _{a}^{{-\varepsilon }}{\frac {3x^{2}}{x^{3}}}\,{\mathrm d}x+\int _{{\varepsilon }}^{b}{\frac {2x}{x^{2}}}\,{\mathrm d}x{\biggr )}=\lim _{{\varepsilon \to 0+}}{\biggl (}\ln {\biggl |}{\frac {b^{2}}{a^{3}}}{\biggr |}+\ln \varepsilon {\biggr )}=-\infty$

Basierend auf einem Artikel in:

Wikipedia.de