Lindemann-Mechanismus

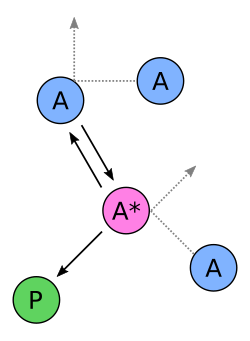
Die Fall-off-Kurve im Lindemann-Mechanismus. Die markierten Bereiche dienen nur der Veranschaulichung, es handelt sich um keine real existierenden Grenzen.

In der Kinetik ist der Lindemann-Mechanismus, der manchmal auch als Lindemann-Hinshelwood-Mechanismus bezeichnet wird, ein schematischer Reaktionsmechanismus für Reaktionen in der Gasphase. Das Konzept wurde 1921 von Frederick Lindemann vorgeschlagen und von Cyril Norman Hinshelwood entwickelt.^[1]^[2] Eine scheinbar unimolekulare Reaktion wird dabei in zwei elementare Schritte zerlegt. Der Lindemann-Mechanismus wird verwendet, um Gasphasenzersetzungs- oder -isomerisierungsreaktionen darzustellen. Die Reaktionsgleichungen von Zersetzungs- oder Isomerisierungsreaktionen lassen häufig vermuten, dass eine unimolekulare Reaktion vorliegen könnte:

${\mathrm {A} {}\mathrel {\longrightarrow } {}\mathrm {P} }$

Doch der Lindemann-Mechanismus zeigt, dass dem unimolekularen Reaktionsschritt ein bimolekularer Aktivierungsschritt vorausgeht. Für bestimmte Fälle ergibt sich daher eine Reaktion zweiter und nicht, wie zu erwarten wäre, erster Ordnung:^[3] Wechselwirken zwei Moleküle ${\mathrm {A} }$ und ${\mathrm {A} }$ miteinander, so kann es zur Bildung eines angeregten Moleküls ${\ce {A}}^{*}$ kommen.^[4]^[5] Das angeregte Molekül kann nun entweder wieder desaktiviert werden, indem es mit anderen Molekülen ${\mathrm {A} }$ wechselwirkt (dies stellt die Rückreaktion dar), oder unimolekular und irreversibel zu Produkt ${\mathrm {P} }$ reagieren. Die Geschwindigkeitskonstanten werden hier mit $k_{1}$ , $k_{-1}$ und $k_{2}$ bezeichnet:^[4]^[5]

${\rm {A+A\ {\overset {k_{1}}{\underset {k_{-1}}{\rightleftarrows }}}\ A^{*}+A}}$

${\rm {A^{*}\ {\overset {k_{2}}{\rightarrow }}\ P}}$

Findet der unimolekulare Schritt so langsam statt, dass er geschwindigkeitsbestimmend ist, beobachtet man eine Reaktion erster Ordnung.^[5]

Geschwindigkeitsgesetz

Schema des Lindemann-Hinshelwood-Mechanismus: Zwei Moleküle ${\mathrm {A} }$ können wechselwirken und ein angeregtes Molekül ${\ce {A}}^{*}$ bilden. Dieses kann entweder durch eine Rückreaktion desaktiviert werden, oder unimolekular und irreversibel zu Produkt ${\mathrm {P} }$ reagieren.

Die Geschwindigkeit, mit der das Produkt ${\mathrm {P} }$ gebildet wird ergibt sich aus dem Bodenstein’schen Quasistationaritätsprinzip. Wir nehmen hierbei an, dass die Konzentration des aktivierten Eduktes (das Intermediat ${\ce {A}}^{*}$ ) in gleicher Geschwindigkeit gebildet wie verbraucht wird.^[6] Diese Annahme vereinfacht die Formulierung der Geschwindigkeitsgleichung der Gesamtreaktion. Die Geschwindigkeitskonstante der Hinreaktion des ersten Schritts bezeichnen wir mit $k_{1}$ , die Rückreaktion mit $k_{-1}$ . Die Geschwindigkeitskonstante der Hinreaktion des zweiten Schritts bezeichnen wir mit $k_{2}$ .

Die Geschwindigkeit, mit der ${\ce {A}}^{*}$ gebildet wird, ergibt sich somit durch folgendes differentielles Geschwindigkeitsgesetz:

${\frac {\mathrm {d} [{\ce {A}}^{*}]}{\mathrm {d} t}}=k_{1}[{\ce {A}}]^{2}$ (Hinreaktion im ersten Schritt)

${\ce {A}}^{*}$ wird sowohl bei der Rückreaktion als auch bei der Produktbildung im zweiten Schritt verbraucht. Es ergeben sich folgende differentielle Geschwindigkeitsgesetze:

${\frac {-\mathrm {d} [{\ce {A}}^{*}]}{\mathrm {d} t}}=k_{-1}[{\ce {A}}^{*}][{\ce {A}}]$ (Rückreaktion im ersten Schritt)

${\frac {-\mathrm {d} [{\ce {A}}^{*}]}{\mathrm {d} t}}=k_{2}[{\ce {A}}^{*}]$ (Hinreaktion im zweiten Schritt)

Insgesamt betrachtet ergibt sich:

${\frac {\mathrm {d} [{\ce {A}}^{*}]}{\mathrm {d} t}}=k_{1}[{\ce {A}}]^{2}-k_{-1}[{\ce {A}}][{\ce {A}}^{*}]-k_{2}[{\ce {A}}^{*}]$

Nach dem Quasistationaritätsprinzip ist die Bildung von ${\mathrm {A} }^{*}$ gleich dem Verbrauch von ${\mathrm {A} }^{*}$ :

${\frac {\mathrm {d} [{\ce {A}}^{*}]}{\mathrm {d} t}}=k_{1}[{\ce {A}}]^{2}-k_{-1}[{\ce {A}}][{\ce {A}}^{*}]-k_{2}[{\ce {A}}^{*}]\approx 0$

Daher ergibt sich:

$k_{1}[{\ce {A}}]^{2}=k_{-1}[{\ce {A}}^{*}][{\ce {A}}]+k_{2}[{\ce {A}}^{*}]$

Aufgelöst nach $[{\ce {A}}^{*}]$ :

$[{\ce {A}}^{*}]={\frac {k_{1}[{\ce {A}}]^{2}}{k_{-1}[{\ce {A}}]+k_{2}}}$

Das differentielle Geschwindigkeitsgesetz ergibt so für die Gesamtreaktion:^[7]^[6]

${\frac {\mathrm {d} [{\ce {P}}]}{\mathrm {d} t}}=k_{2}[{\ce {A}}^{*}]={\frac {k_{1}k_{2}[{\ce {A}}]^{2}}{k_{-1}[{\ce {A}}]+k_{2}}}$

Dieses Geschwindigkeitsgesetz ist (noch) keine Reaktion erster Ordnung bezüglich ${\mathrm {A} }$ .^[5] Wenn jedoch die Desaktivierung angeregter ${\ce {A}}^{*}$ -Moleküle durch die Rückreaktion schneller erfolgt als die unimolekulare Reaktion zum Produkt ${\mathrm {P} }$ ,

$k_{-1}{\rm {[A][A^{*}]}}\gg k_{2}{\rm {[A^{*}]}}$

so kann man $k_{2}$ im Nenner vernachlässigen. Fasst man die Konstanten $k_{1}$ , $k_{-1}$ und $k_{2}$ zu einer Konstante $k_{\mathrm {R} }$ zusammen, gilt näherungsweise:

${\frac {\mathrm {d} [{\mathrm {P} }]}{\mathrm {d} t}}\approx {\frac {k_{1}k_{2}[{\mathrm {A} }]^{2}}{k_{-1}[{\mathrm {A} }]}}={\frac {k_{1}k_{2}[{\mathrm {A} }]}{k_{-1}}}=k_{\mathrm {R} }[{\mathrm {A} }]$

Dies ist ein Geschwindigkeitsgesetz erster Ordnung.^[5]

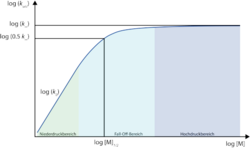
Reaktionsordnung

Die Reaktionsordnung einer Reaktion, die annähernd dem Lindemann-Mechanismus folgt, ist druckabhängig. Bei hohem Druck (Hochdruckgrenzwert $k_{\infty }$ für $[{\ce {A}}]\rightarrow \infty$ ) handelt es sich um eine Reaktion erster und bei niedrigem Druck (Niederdruckgrenzwert $k_{0}$ für $[{\ce {A}}]\rightarrow 0$ ) um eine Reaktion zweiter Ordnung.

Siehe auch

Kinetik (Chemie)

Einzelnachweise

↑ Francesco Di Giacomo: A Short Account of RRKM Theory of Unimolecular Reactions and of Marcus Theory of Electron Transfer in a Historical Perspective. In: Journal of Chemical Education. Band 92, Nr. 3. ACS, 10. März 2015, S. 476–481, doi: 10.1021/ed5001312.
↑ F. A. Lindemann, Svante Arrhenius, Irving Langmuir, N. R. Dhar, J. Perrin, W. C. McC. Lewis: Discussion on “the radiation theory of chemical action”. In: Transactions of the Faraday Society. Band 17, 1922, S. 598–606, doi: 10.1039/TF9221700598.
↑ "Gas phase decomposition by the Lindemann mechanism" by S. L. Cole and J. W. Wilder. SIAM Journal on Applied Mathematics, Vol. 51, No. 6 (Dec., 1991), S. 1489–1497.
↑ ^{Hochspringen nach: a} ^b Gerd Wedler, Hans-Joachim Freund: Lehr- und Arbeitsbuch Physikalische Chemie. Siebte, wesentlich überarbeitete und erweiterte Auflage. Weinheim 2018, ISBN 978-3-527-34611-0, S. 541 f.
↑ ^{Hochspringen nach: a} ^b ^c ^d ^e Peter W. Atkins: Physikalische Chemie. 5. Auflage. Weinheim 2013, ISBN 978-3-527-33247-2, S. 860 f.
↑ ^{Hochspringen nach: a} ^b Atkins P. and de Paula J., Physical Chemistry (8th ed., W.H. Freeman 2006) S. 820-1, ISBN 0-7167-8759-8.
↑ Steinfeld J.I., Francisco J.S. and Hase W.L. Chemical Kinetics and Dynamics (2nd ed., Prentice-Hall 1999), S. 335, ISBN 0-13-737123-3.

Basierend auf einem Artikel in:

Wikipedia.de