Leitungsbeläge
Zu den elektrischen Kenngrößen einer elektrischen Leitung gehören außer dem Leitungswellenwiderstand die sogenannten Leitungsbeläge. Leitungsbeläge beschreiben die Kapazität, die Induktivität, den Längswiderstand in Leitungsrichtung und den Querleitwert quer zur Leitungsrichtung einer Leitung bezogen auf die Leitungslänge. Die Leitungsbeläge sind längenbezogene, zusammengefasste elektrische Eigenschaften abhängig von Material und Geometrie. Sie sind in erster Näherung Konstanten eines Kabeltyps - falls sich dieser im freien Raum befindet. Aus diesem Grund werden sie auch als „primäre Leitungskonstanten“ (im Gegensatz zu den „sekundären Leitungskonstanten“ Wellenwiderstand und Fortpflanzungskonstante) bezeichnet.
Ersatzschaltbild
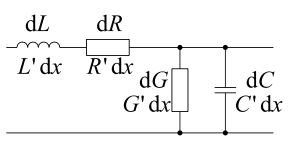
Das Bild zeigt das Ersatzschaltbild eines Leitungsabschnitts, der sich nach
der infinitesimalen Länge
jeweils wiederholt, siehe Leitungstheorie.
Der Widerstandsbelag
,
der Ableitungsbelag
,
der Kapazitätsbelag
und der Induktivitätsbelag
stehen für die gleichmäßig über eine homogene Leitung mit der Länge
verteilten Größen. Zur Unterscheidung von den Größen
eines diskreten Bauelements (auch einer konkreten Leitung) werden die
längenbezogenen Leitungsbeläge durch einen Strich gekennzeichnet.
Beläge
Zur Bestimmung der Beläge einer homogenen Leitung ist die Länge der betrachteten Leitung frei wählbar. Angaben für einen Kapazitätsbelag von beispielsweise
- 0,067 μF pro km oder 67 pF pro m oder 1 μF pro 14,9 km
sind zulässig und untereinander gleichwertig. Eine Leitung heißt homogen, wenn ihre Beläge über ihre Länge konstant sind.
Widerstandsbelag R'
Der Widerstandsbelag
hat die Einheit
Ohm
pro Meter
.
Er beschreibt den ohmschen
Widerstand
einer elektrischen
Leitung bezogen auf ihre Länge
.
Mit dem spezifischen
Widerstand
und der Querschnittsfläche
gilt für einen einzelnen Leiter
.
Tatsächlich muss man bei einer Zweidrahtleitung Hin- und Rückleiter mit
eventuell unterschiedlichen Parametern beachten. Deshalb folgt beispielsweise
für eine symmetrische Doppelleitung
.
Diese „gleichstrommäßige“ Berechnung gilt aber nur für relativ niedrige Frequenzen, denn aufgrund der Stromverdrängung durch den Skineffekt verringert sich die Eindringtiefe und der Widerstandsbelag steigt mit der Frequenz an.
Ableitungsbelag G'
Der Ableitungsbelag
hat die Einheit Siemens
pro Meter;
.
Er beschreibt die Verluste durch unvollständige Isolation pro Länge. Bei den typisch auftretenden Spannungen und Strömen sind die relativen Stromverluste durch den Ableitungsbelag deutlich geringer als die relativen Spannungsverluste durch den Widerstandsbelag.
Kapazitätsbelag C'
Der Kapazitätsbelag
hat die Einheit Farad pro Meter;
.
Er ist die Kapazität einer Leitung pro Länge dieser Leitung. Der
Kapazitätsbelag lässt sich aus der Permittivität
(früher Dielektrizitätskonstante) und der Geometrie der Leitungsanordnung
berechnen. Beispielsweise hat eine Zweidrahtleitung mit
einem Drahtdurchmesser
und einem Drahtabstand
den Kapazitätsbelag
, bzw.
.
Oft ist eine geringe Leitungskapazität erwünscht, um z.B. das
Übersprechen von
Signalleitungen oder die während jeder Netzperiode gespeicherte Energie (Blindleistung) in
Versorgungsnetzen gering zu halten. Dies lässt sich durch eine niedrige
Permittivität
und/oder einen großen Drahtabstand
im Vergleich zum Drahtdurchmesser
erreichen. Zu erheblichen Problemen durch den Kapazitätsbelag siehe
beispielsweise die 380-kV-Transversale
Berlin.
Induktivitätsbelag L'
Der Induktivitätsbelag
hat die Einheit Henry
pro Meter;
.
Er stellt den Induktivitätswert pro Länge dar. Beispielsweise hat die zuvor
genannte Zweidrahtleitung mit der Permeabilität
(früher Induktionskonstante) den Induktivitätsbelag
, bzw.
.
Während im Allgemeinen zur Berechnung des Induktivitätsbelags auch die innere Induktivität der Leiter beachtet werden muss, ist das bei höheren Frequenzen aufgrund der Stromverdrängung durch den Skineffekt nicht nötig.
Je nach Anwendung und geforderter Impedanz kann eine hohe oder eine niedrige
Leitungsinduktivität wünschenswert sein. Ein Beispiel der Erhöhung der
Leitungsinduktivität zum Erreichen einer hohen Impedanz ist das Krarupkabel. Soll der
Induktivitätsbelag – z.B. zur Übertragung von hohen Stromimpulsen −
möglichst gering sein, kann dies durch eine niedrige Permeabilität
oder geringe Abstände
zwischen Hin- und Rückleiter erreicht werden. Besonders geringe
Induktivitätsbeläge sind mit eng aneinanderliegenden Bandleitern erreichbar.
Allerdings erhöht sich mit sinkendem Drahtabstand der Kapazitätsbelag in
demselben Maße wie sich der Induktivitätsbelag erniedrigt. Eine Verringerung der
Induktivität lässt sich auch durch das Parallelschalten mehrerer Leitungen
erzielen.
Anwendung
Der oben genannte Leitungswellenwiderstand ist beim Betrieb mit sinusförmiger Wechselspannung und der Anwendung der komplexen Wechselstromrechnung durch die Leitungsbeläge festgelegt (j ist hier die imaginäre Einheit):


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.07. 2022