Waagerechter Wurf

Unter dem waagerechten (auch waagrechten) beziehungsweise horizontalen Wurf versteht man in der Physik den Bewegungsvorgang, den ein Körper vollzieht, wenn er parallel zum Horizont geworfen oder geschossen wird, sich also mit einer horizontalen Startgeschwindigkeit nur unter dem Einfluss seiner Gewichtskraft bewegt. Die resultierende Bahnkurve ist eine Wurfparabel mit dem Abwurfort als Scheitel.
Der waagrechte Wurf lässt sich nach dem Superpositionsprinzip (Unabhängigkeitsprinzip) in zwei Teilbewegungen zerlegen, die Bewegung in x-Richtung und in y-Richtung beeinflussen sich gegenseitig nicht. Dies funktioniert aber nur dann, wenn man den Wurf unter idealisierten Bedingungen, also etwa ohne Berücksichtigung des Luftwiderstandes betrachtet.
Typische Beispiele sind der Wurf eines Körpers mit horizontaler Anfangsgeschwindigkeit im Schwerefeld (Stoß einer Kugel von einem Tisch, Wasserstrahl spritzt aus waagrecht gehaltenem Schlauch, Abwurf eines Körpers aus horizontal fliegendem Flugzeug) oder die Bahn eines geladenen Teilchens in einem homogenen elektrischen Feld (z.B. Elektron im Plattenkondensator einer Kathodenstrahlröhre).
Analyse der Bewegung
In (waagerechter) x-Richtung
Wird ein Körper zum Beispiel von einem Tisch gestoßen, verlässt er diesen mit der konstanten Geschwindigkeit v0 in horizontaler Richtung. Für diese Komponente der Bewegung gelten also die Gesetze der gleichförmigen Bewegung:
(Ortskoordinate),
(Geschwindigkeit in x-Richtung), sowie
(Beschleunigung in x-Richtung).
In (senkrechter) y-Richtung
Gleichzeitig fällt der Körper aus der (Anfangs-/Start-)Höhe h0 nach unten. Es gelten die Gesetze des freien Falls, der Körper führt eine Bewegung mit konstanter Beschleunigung (der Erdbeschleunigung g) aus:
(Ortskoordinaten),
(Geschwindigkeit in y-Richtung) und
(Beschleunigung in y-Richtung).
Gleichung der Wurfparabel
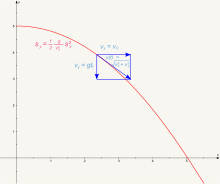
Für die Gleichung der Wurfparabel (Bahnkurve beziehungsweise Ortskurve), der Bahn-Trajektorie, löst man die sx-Gleichung nach t auf und setzt den Term für t in die sy-Gleichung ein. So erhält man:
,
bzw.
.
Allgemein schreibt man:
.
Wurfweite
Damit kann man die Formel für die Wurfdauer in die
-Gleichung einsetzen und erhält so die Wurfweite:
Wurfhöhe
Der Subtrahend (bzw. Summand) in der Gleichung der Bahnkurve entspricht der Wurfhöhe (Anfangshöhe), wenn für sx die Wurfweite sw eingesetzt wird:
Wurfdauer
Setzt man die sy-Gleichung
und löst sie nach t auf, so erhält man die Zeit (Wurfdauer, Wurfzeit, Flugdauer, Flugzeit) des Körpers, bevor er auf den Boden fällt:
Aufprallwinkel
Wenn man den Winkel der Bahnkurve zur Horizontalen mit
bezeichnet, dann kann man diesen Winkel aus der folgenden Beziehung berechnen:
Bahngeschwindigkeit
Der Betrag der Bahngeschwindigkeit
(und die Aufprall- beziehungsweise Endgeschwindigkeit am Ende der Wurfzeit) lässt
sich mit dem Satz des Pythagoras errechnen:
sowie
.
Realer Fall
Wenn die Reibung berücksichtigt werden muss, kann eine näherungsweise Berechnung der Bahn noch auf Schulniveau beispielsweise mithilfe der Methode der kleinen Schritte erfolgen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.03. 2024