Schnittreaktion
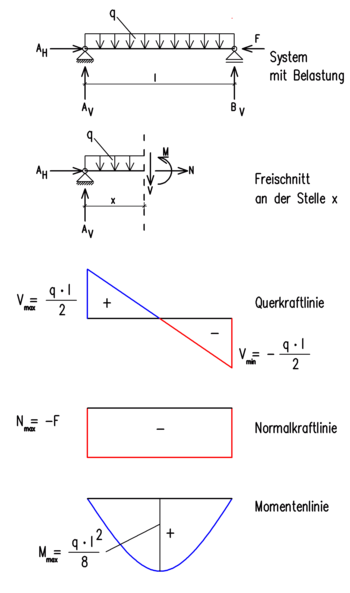
Schnittreaktionen an einer Schnittstelle im zweiten Teilbild: Normalkraft N, Querkraft V, Biegemoment M.
Die folgenden 3 Liniendiagramme (Zustandslinien) zeigen die über die Balkenlänge an der variablen Stelle x auftretenden Schnittreaktionen (ebenfalls die Schnittgrößen).
Die
Schnittreaktionen sind die in der Mechanik
beim Schnittprinzip
(auch Freischneiden
genannt) angewendeten an der Schnittfläche eines festen oder flüssigen Objekts
gedanklich anzubringenden, das Gleichgewicht haltenden Gegen-Kräfte und Gegen-Momente. Sie halten den am
verbliebenen Objekt angreifenden äußeren Kräften und Momenten (eingeprägte
Kräfte und Momente samt Lagerreaktionen)
das Gleichgewicht. Die Schnittreaktionen können auch als Lagerreaktionen (daher
Schnittreaktion) einer die Schnittfläche des verbleibenden Objekts
stützenden gedachten Lagerung aufgefasst werden oder – gleichwertig –
als Kräfte und Momente, mit denen das entfernte Objekt auf die Schnittfläche des
verbleibenden Objekts einwirkt.
Die Schnittreaktionen sind die an der Schnittstelle sichtbar gemachten, für Festigkeits- und Verformungsuntersuchungen benötigten inneren Kraftgrößen bzw. die als Schnittgrößen bezeichneten inneren Kräfte und Momente im nur gedanklich geschnittenen Objekt.
Die Schnittgrößen in einem z.B. festen stabförmigen Bauteil im ebenen Kraftsystem sind:
- eine parallel zur Stabachse wirkende Kraft (Normalkraft),
- eine normal zur Stabachse wirkende Kraft (Querkraft),
- ein Biegemoment.
Befindet sich das stabförmige Bauteil in einem räumlichen Kraftsystem, so wird die Querkraft vorteilhaft mit zwei Komponenten in einem rechtwinkligen Koordinatensystem (x-Achse gleich Stabachse) angegeben. Das Moment hat drei Komponenten, zwei Biegemomente und ein in der Stabachse drehendes Torsionsmoment.
Anwendung des Schnittprinzips an einem festen, stabförmigen Bauteil
Man kann einen belasteten Stab an jeder beliebigen Stelle gedanklich schneiden und nur einen der Schnittteile untersuchen. Die Schnittebene ist eben und senkrecht zur Stabachse. Der Einfluss des weggeschnittenen Teils auf den zu untersuchenden Teil wird durch an der Schnittstelle anzubringenden Kräfte und Momente - den Schnittreaktionen bzw. Schnittgrößen - repräsentiert. Das zu untersuchende Teil bleibt mit Hilfe der Schnittgrößen im Gleichgewicht.
Man kann auch ein beliebiges Teil herausschneiden, d.h. zwei Schnitte machen. Schnittgrößen sind dann an beiden Schnittflächen anzubringen.
Beim gedanklichen Schneiden entsteht eine (unendlich kleine) Lücke, der man zwei Ufer - ein linkes und ein rechtes - zuordnen kann. Demzufolge kann an Stelle des Terminus Schnittfläche auch der Begriff Schnittufer verwendet werden. Die Schnittfläche am linken Ende des zu untersuchenden Teils ist ein rechtes Schnittufer, am rechten Ende ein linkes Schnittufer. Anstatt der Adjektive links und rechts verwendet man aber im Zusammenhang mit der Wahl des Koordinatensystems die Adjektive positiv und negativ.
Die Schnittfläche mit Normalenvektor in positive x-Richtung wird zum positiven Schnittufer. Dabei zeigen alle Schnittgrößen in positive Richtung. Die Normalkraft N zeigt in positive x-Richtung, die Querkraft Q in positive z-Richtung und das Biegemoment besitzt einen positiven Drehsinn (Linksdrehung). Es liegt dann also eine Drehung um die y-Achse entgegen des Uhrzeigersinns (gleich positiver Drehsinn) vor.
Zeigt der Normalenvektor der Schnittfläche in negative x-Richtung, so spricht man entsprechend von einem negativen Schnittufer. In diesem Fall zeigen alle Schnittgrößen in negative Richtung, und das Biegemoment dreht sich um die y-Achse im Uhrzeigersinn (gleich negativer Drehsinn).
Schnittreaktionen in der Ebene
Alle hier durch Pfeile dargestellten Schnittreaktionen (Kräfte und Momente) sind nach üblicher Vorzeichenkonvention positiv angetragen.
Die Bezugsfaser wird als gestrichelte Linie dargestellt.
Die Lage des lokalen Stabachsenkoordinatensystems wird durch die gestrichelte Faser (gleich Bezugsfaser) skizziert. Sie legt die Richtung, als auch den Ursprung der x-,y- und z-Achse sowie die Lage der y- und z-Achse fest. Nach üblicher Konvention gilt: Die z-Achse zeigt zur gestrichelten Seite hin. Die x-Achse ist die Stabachse. Die y-Achse zeigt aus der Ebene heraus. Damit ergibt sich die Richtung der x-Achse eines kartesischen Rechtskoordinatensystems automatisch.
- Querkraft – Eine Kraft senkrecht zur x-Achse des Bauteils. Häufige Notationen sind V (vertikal), FQ, Q (quer), Fy/Fz (in y-/z-Richtung)
- Normalkraft oder Längskraft – Eine Kraft parallel zur x-Achse des Bauteils. Notationen sind N, FN (normal = senkrecht), FL (Längs)
- (Biege-)Moment – Das an der Schnittstelle wirkende Moment. Im ebenen Fall wird es einfach mit M bezeichnet.
Alle Schnittreaktionen sind Vektorgrößen. Das heißt, dass jede Kraft eine Richtung hat und jedes Moment entweder im oder gegen den Uhrzeigersinn dreht.
Ein Stab oder ein komplexeres Objekt kann auch in einem Gelenk freigeschnitten werden. Dabei gilt:
- Das Reaktions-Moment an einem „Momentengelenk“ ist Null.
- Die Reaktions-Querkraft an einem „Querkraftgelenk“ ist gleich der dort eingeprägten Kraft.
- Die Reaktions-Normalkraft an einem „Normalkraftgelenk“ ist gleich der dort eingeprägten Kraft.
Schnittreaktionen im Raum
Die Reaktions-Querkraft und das -Biegemoment erscheinen im kartesischen Koordinatensystem als je zwei Komponenten. Das Reaktions-Moment enthält eine dritte Komponente, nämlich eine um die x-Achse drehende (Torsionsmoment, Notationen sind Mx, MT oder T).
Zustandslinien
Verschiebt man die gedachte Schnittstelle entlang des Bauteiles, so ändern sich die Schnittreaktionen. Die in einem Diagramm dargestellten Schnittreaktionen als Funktion des Schnittstellen-Ortes (Koordinate x, s. Bild in der Einleitung) nennt man Zustandslinien, da die Schnittreaktionen dem an dieser Stelle bestehenden inneren Zustand (mechanische Spannungen) entsprechen. Die Stellen der stärksten Beanspruchung in einem Balken mit konstantem Querschnitt treten in den Zustandslinien deutlich hervor.
Einflusslinien
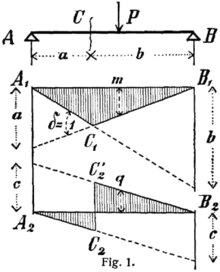
Eine Einflusslinie stellt im Unterschied zur Zustandslinie z.B. nicht eine Schnittreaktion in Abhängigkeit von der Schnittstelle (Koordinate x) sondern die Abhängigkeit einer Schnittreaktion an einem bestimmten Ort (Koordinate x0) vom veränderlichen Ort (Koordinate x) eine äußeren Last dar.
Einer ortsveränderlichen Last sind z.B. Brücken durch ein darüber rollendes Fahrzeug unterworfen. Es interessiert der Einfluss der variablen Stelle der Last auf die Beanspruchung der Brücke an einer bestimmten Stelle (Koordinate x0 in Fahrtrichtung), die z.B. durch die Größe der Schnittreaktionen an einem dort gedachten Schnitt ausgedrückt wird.
Nebenstehende Abbildung lässt erkennen, dass Einflusslinien i.d. R. aus Geraden bestehen.
Berechnen der Schnittreaktionen
Um Schnittreaktionen zu berechnen, gibt es mehrere Möglichkeiten. Bei allen müssen die Gleichgewichtsbedingungen eingehalten werden. Generell unterscheidet man:
geschlossenes Krafteck
Man kann das Krafteck rechnerisch oder graphisch lösen.
Die Gleichgewichtsbedingungen liefern im Allgemeinen nur bei statisch bestimmten Systemen eindeutige Ergebnisse. Bei statisch unbestimmten Systemen gibt es im Allgemeinen zu viele Unbekannte, um sie ohne zusätzliche Gleichungen anzuwenden. In diesem Fall führen z.B. Kraft- oder Weggrößenverfahren zur Lösung. Die Schnittreaktionen (an statisch bestimmten Systemen) rechnet man normalerweise mithilfe der Gleichgewichtsbedingungen aus. Die Gleichgewichtsbedingungen für statische Systeme besagen, dass
- die Summe aller Kräfte gleich null ist
und
- die Summe aller Momente (um einen beliebigen Punkt) gleich null ist
.
Mit diesen Gleichgewichtsbedingungen werden Gleichungen erstellt, die es ermöglichen, die fehlenden Kräfte oder Momente auszurechnen. Durch eine intelligente Wahl der Schnitte (z.B. so, dass jeweils nur eine unbekannte Größe in einer Gleichung auftaucht) lässt sich oft der Rechenaufwand verringern, jedoch ist dies nicht immer möglich.
Die genauen Gleichungen sind im Folgenden aufgeführt.
Ebener Fall (2D)
Hier kann man 3 linear unabhängige Momenten-Gleichgewichtsbedingungen definieren, am einfachsten ist es im Allgemeinen zwei Punkte davon im Unendlichen zu definieren und somit erhält man zwei Kraftkomponenten-Gleichgewichtsbedingungen und eine Momenten-Gleichgewichtsbedingung:
Anmerkung: Der Index „A“ in der Momentegleichung deutet darauf, dass man hier die Summe der Momente um einen fiktiven Drehpunkt „A“ betrachtet.
Allgemeiner Fall (3D)
Hier ergeben sich z.B. drei Kraftkomponenten-Gleichgewichtsbedingungen und drei Momentenkomponenten-Gleichgewichtsbedingungen:
Die Punkte „A1“, „A2“, „A3“ dürfen auch identisch sein, sondern liefern auch neue linear unabhängige Gleichungen, da sie die Drehmomente um eine andere Achse betrachten. Alternativ kann z.B. man auch sechs Momenten-Gleichgewichtsbedingungen aufstellen, hierbei muss man jedoch unterschiedliche Punkte wählen.
Schnittgrößendifferentialgleichungen
Mit diesem Ansatz werden Differentialgleichungen, die die Gleichgewichtsbedingungen erfüllen, für die gesuchten Schnittgrößen aufgestellt und dann mit zum System passenden Randbedingungen (beispielsweise: Keine Momentübertragung an einem Lager an Position x=0) gelöst.
In der schubweichen Balkentheorie II. Ordnung gibt es unter den Bernoullischen Annahmen folgende Differentialgleichungen für die Queranteile:
mit
- der Laufkoordinate x entlang der Balkenachse
- dem Elastizitätsmodul E
- dem Schubmodul G (Term tritt in der schubstarren Theorie nicht in den Differentialgleichungen auf)
- dem Flächenträgheitsmoment I(x)
- R(x) der Transversalkraft (in der Theorie I. Ordnung gilt R(x)=V(x))
- V(x) der Querkraft
- NII(x) die Normalkraft nach Theorie Theorie II. Ordnung (in der Theorie I. Ordnung tritt dieser Term in der Differenzialgleichung nicht auf)
- q(x) der Gleichlast (Querbelastung pro Längeneinheit)
- M(x) dem Biegemoment
- m(x) dem Steckemoment (Biegebelastung pro Längeneinheit)
- φ(x) der Verdrehung
- κe(x) der eingeprägten Krümmung
- w(x) der Durchbiegung zufolge Belastung
- wv(x) der Durchbiegung zufolge Vorverformung
der Schubfläche (Term tritt in der schubstarren Theorie nicht auf).
Die ersten beiden Differenzialgleichungen folgen allein aus den Gleichgewichtsbedingungen, erste folgt aus Summe der Vertikalkräfte ist null und zweitere aus der Erkenntnis dass die Summe der Momente muss Null sein muss. Die letzten beiden Differenzialgleichungen sind geometrische Differentialbeziehungen, das die erste Ableitung der Biegelinie die Neigung ist und die zweite Ableitung die Krümmung ist, hinzukommend werden hier noch zwei Materialgleichungen eingesetzt:
und
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.04. 2024