Baustatik

Baustatik oder die Statik der Baukonstruktionen ist die Lehre von der Sicherheit und Zuverlässigkeit von Tragwerken im Bauwesen. In der Baustatik werden die Kräfte und deren gegenseitige Auswirkungen in einem Bauwerk sowie in jedem dazugehörigen Bauteil berechnet. Die Berechnungsverfahren der Baustatik sind Hilfsmittel der Tragwerksplanung und mit der Lehre der Modellbildung und der Konstruktionslehre Teil der Tragwerkslehre.
Die Baustatik ist eine Sammlung rechnerischer und grafischer Verfahren, welche dazu dienen, bei Bauwerken aus der Einwirkung äußerer Lasten auf Belastungen und Verformungen mit deren Spannungen zu schließen. Die Lastabtragung des sogenannten Tragwerks nachzuvollziehen und damit letztlich dessen Gebrauchstauglichkeit nachzuweisen. (Ein Tragwerk ist die Modellvorstellung der lastabtragenden Teile eines Bauwerks, die sich in Steifigkeit, Festigkeit und Material grundsätzlich unterscheiden können.)
Die auf ein Bauwerk einwirkenden Lasten unterteilt man nach der Häufigkeit ihres Auftretens in ständige (etwa das Eigengewicht der Konstruktion), veränderliche (etwa Schnee, Wind, Temperatur, Verkehr oder schwankende Wasserstände) und außergewöhnliche Einwirkungen (etwa Erdbeben, Feuer oder den Anprall von Fahrzeugen). Diese realen Lasten, werden i.d.R. mithilfe von Normen mit einer gewissen Versagenswahrscheinlichkeit liegend auf der sicheren Seite abgeschätzt. Eine Zielsetzung der Baustatik ist, die ungünstigste Kombination der i.d.R. laut Norm relevanten Kombinationen aus diesen angenommen Lasten zu ermitteln, und zwar hinsichtlich der Tragsicherheit (z. B. Bruch, Plastizitätsvermögen, Knicken) und der Gebrauchstauglichkeit (z.B. Verformungen, Rissbreiten, Schwingungen).
Die Problemstellungen beinhalten hauptsächlich quasistatische Belastungen sowie statische Festigkeitsnachweise und Stabilitätsnachweise, während die verwandte Baudynamik die Reaktion von Konstruktionen auf zeitlich veränderliche Lasten (wie z.B. Wind) erfasst. Wobei dynamische Lasten mit Methoden der Statik berechnet werden können. Diese sogenannte quasistatische Berechnung berücksichtigt die dynamischen Effekte mit Faktoren die groß genug sind damit die so ermittelte Abschätzung sicher auf der richtigen Seite liegt. Im normalen Hochbau werden Schwingungsnachweise im Zuge der baustatischen Berechnung je nach Baustoff mit gewissen Bauwerksabmessungen automatisch als erfüllt betrachtet. (z.B. im europäischen Norm EN 1992 die Grenzschlankheit, welche die Mindestdicke einer Platte in Abhängigkeit einer fiktiven Spannweite und des Bewehrungsgrades vorschreibt, um einen gesonderten Schwingungsnachweis nicht führen zu müssen.)
Als spezielles und spezialisiertes Teilgebiet der Mechanik bedient sich die klassische Baustatik vor allem der Elastizitätstheorie und des Hookeschen Gesetzes, es kann aber genauso in der Plastizitätstheorie, wie der Fließgelenktheorie angewendet werden.
Abgrenzungen und Begriffe
Der Begriff Statik wird mehrdeutig verwendet und betrifft oft die theoretisch-mathematisch-physikalische Seite (Statik als Teilgebiet der Technischen Mechanik), während die Baustatik die Anwendung dieser Statik im Bauwesen zum Ziel hat. Die Planung des Tragwerkes erfolgt i.d.R. ohne baustatische Berechnungen (i.d.R. vom Architekten). Daraus wird üblicherweise ein statisches Model mit dem Lastabtragungsmechanismus definiert, welcher anschließend üblicherweise die Bemessung folgt, also die Festlegung von Abmessungen, Bewehrung etc.
Der verantwortliche Baustatiker oder Tragwerksplaner – heute in der Regel ein Bauingenieur, seltener ein Architekt – wird umgangssprachlich oft als Statiker bezeichnet. Das Ergebnis seiner Überlegungen und Berechnungen, die Statische Berechnung, wird in einigen Zusammenhängen Standsicherheitsnachweis, meist aber verkürzt ebenfalls Statik genannt.
Aufgaben
Die wichtigste Annahme der Baustatik wie der Statik ist, dass sich das Tragsystem im Gleichgewicht befindet. Ein wesentlicher Aspekt der Baustatik ist es, aus einem komplexen Bauwerk ein klar definiertes Tragsystem zu modellieren, das die Nachweise mit einem wirtschaftlich sinnvollem Aufwand erfüllen kann. Zuerst werden die rechnerischen Lasten ermittelt. Daraus ergeben sich rechnerische Schnittgrößen und Verformungen, um eine Bemessung durchzuführen. Die einwirkenden Lasten, welche sich im Zuge einer statischen Annahme jederzeit im Gleichgewicht befinden, werden über die tragenden Bauteile kurzgeschlossen.
Tragwerke
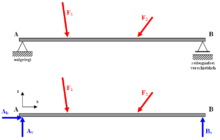
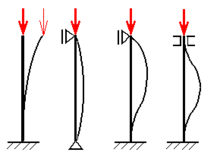
Die Baustatik kennt zwei große Gruppen von Tragwerken:
- Stabwerke (Stäbe, Träger, Stützen, Rahmen, Bogen, Fachwerke)
- Flächentragwerke, bestehend aus Platten, Scheiben, Schalen oder Membranen.
Einwirkungen (Lasten)
Die Einwirkungen (bzw. Lasten), für die ein Tragwerk mittels der Baustatik bemessen werden muss, sind u.a.
- Eigengewicht
- Nutzlast (früher auch Verkehrslast)
- Windlast
- Schneelast
- Wasserdruck
- Erddruck
- Fahrzeuganprall
- Erdbeben; Bemessungskriterien (Erdbeben)
- Eisdruck, Eislast
- Temperatur
- Zwang
Dynamische Lasten (z.B. Stöße, Vibrationen, Erdbeben) und die daraus entstehenden Verformungen (z.B. Vibrationen, Schwingungen) werden im Hochbau und Straßenbau üblicherweise in statische Ersatzlasten umgerechnet, bevor sie auf ein Bauwerk angesetzt werden.
Berechnungsverfahren
Die Berechnungsverfahren in der Baustatik lassen sich unterteilen in:
- Zeichnerische Verfahren (Grafische Statik)
- Rechnerische Verfahren (Starrkörperstatik, Elastizitätslehre, Nichtlineare Stabstatik, …)
- Experimentelle Statik
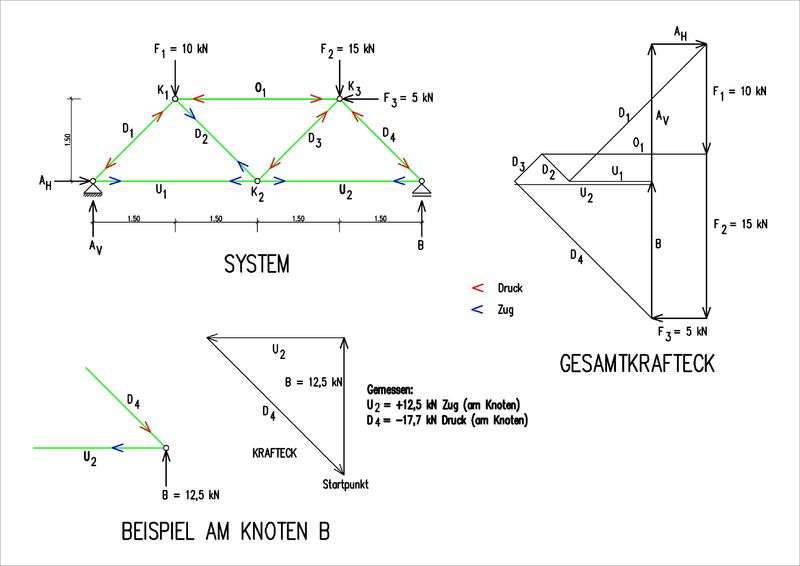
Zeichnerische Verfahren
- Cremonaplan
- Drei-Kräfte-Verfahren
- Culmann-Verfahren
- Seileckverfahren
- Krafteckverfahren
Rechnerische Verfahren
Zu den rechnerischen Verfahren der Baustatik zählen u.a.:
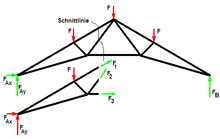
Klassische Verfahren
- Rittersches Schnittverfahren
- Kraftgrößenverfahren
- Weggrößenverfahren
- Formänderungsverfahren
- Momentenausgleichsverfahren
- Drehwinkelverfahren
- Cross-Verfahren
- Kani-Verfahren (Verfahren nach Kani)
- Spannungstrapezverfahren
Matrizenverfahren
- Finite-Elemente-Methode (FEM)
- Finite-Differenzen-Methode (FDM)
- Randelemente-Methode (REM) (=Boundary Element Method, BEM)
- Discrete element method (DEM) (=Distinct element method)
Computer-Berechnungen
Für Konrad Zuse waren die gute Formalisierbarkeit und der hohe Zeitaufwand statischer Berechnungen die ursprüngliche Motivation, programmierbare Rechner zu entwickeln. Statische Berechnungen gehörten darum von Anfang an zu den Computer-Anwendungen, die nach und nach zu statischen Bemessungsprogrammen für jeden Zweck führten. Statische Berechnungen werden heute fast nur noch mit Computerprogrammen erstellt. Die untersuchten statischen Modellbildungen werden oftmals komplexer und anspruchsvoller. Die Berechnung von ebenen Flächentragwerken wie Deckenplatten, elastisch gebetteten Platten, Wandscheiben etc. ist heute in der Praxis eine Routineaufgabe. Mit der Finite-Elemente-Methode werden i.d.R. kompliziertere Tragwerke wie Membran- und Schalentragwerke untersucht.
Erweiterte Technische Biegelehre
Die Technische Biegelehre wurde derart erweitert, dass für die allgemeine Schnittgrößenkombination (N, My, Mz, Vz, Vy, T) der zugehörige Verzerrungszustand auch bei nichtlinearem Werkstoffverhalten berechnet werden kann. Er ist ebenfalls eine Dehnungsebene, die infolge der zu berücksichtigenden Gleitung zusätzlich noch verwölbt wird. Bei der Erweiterten Technischen Biegelehre (ETB) werden analog der Technischen Biegelehre die notwendigen Bedingungen von Gleichgewicht und geometrischer Verträglichkeit bei realistischem Werkstoffverhalten erfüllt. Die Anwendung der ETB macht die getrennten Nachweise Biegebemessung und Schubbemessung überflüssig.
Theorie I., II. oder III. Ordnung
Bei Anwendung der sogenannten Theorie I. Ordnung werden die im Balkenquerschnitt herrschenden Gleichgewichte zwischen Belastung (Kräfte und Momente) und Beanspruchung (Spannungen) am unverformten Balken betrachtet. Der Einfluss der Verformung (inkl. eventueller geringer Vorverformung) wird vernachlässigt. Diese Vorgehensweise ist i.d.R. nur dann zulässig, wenn die Verformungen so klein sind, dass sie die Ergebnisse der Berechnung nur unwesentlich beeinflussen.
Wenn die Änderung der Schnittgrößen und damit auch der Verformungen und Spannungen nicht vernachlässigt werden kann, muss bei der Berechnung die Geometrie des verformten Tragwerkes berücksichtigt werden. Dabei ist es im Allgemeinen außerdem erforderlich, auch die ungewollten Abweichungen des Tragwerkes von der geplanten Geometrie (z.B. Schiefstellung von Stützen) und die Vorverformungen der Bauteile (z.B. Krümmung von Druckstäben) zu berücksichtigen. Die zu berücksichtigende Größe dieser Imperfektionen im Bauingenieurwesen ist in Normen vorgeschlagen.
Bei der sogenannten Theorie II. Ordnung wird i.d.R. angenommen, dass die Verformungen eines Bauteils klein sind. Dies stellt im Bauwesen die Regel dar, denn große Verdrehungen führen unter anderem dazu, dass die Gebrauchstauglichkeit i.d.R. nicht mehr gegeben ist. Bei der linearisierten Theorie II. Ordnung folgen aus der Annahme kleiner Verdrehungen (φ) die Vereinfachungen sin φ = φ und cos φ = 1.
Seltener ist es erforderlich, auch große Verformungen eines Tragwerkes zu erfassen. Ein Beispiel dafür ist die Berechnung von Seilnetzen. In diesem Fall spricht man von einer Berechnung nach Theorie III. Ordnung. Die Vereinfachungen der Theorie II. Ordnung gelten dann nicht mehr. In machen Bücher kann man auch noch eine Theorie IV. Ordnung finden, die z.B. das Nachbeulverhalten erläutert. Es gibt keine klare Abtrennung, der Theorie II. Ordnung und Theorie III. Ordnung, weshalb man manchmal auch nur von der Theorie I. und II. Ordnung spricht.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.08. 2024