Numerische Differentiation

Fehlerverhalten der numerischen Differentiation

In der Numerischen Mathematik bezeichnet man mit numerischer Differentiation die näherungsweise Berechnung der Ableitung aus gegebenen Funktionswerten, meist mittels eines Differenzenquotienten. Dies ist nötig, falls die Ableitungsfunktion nicht gegeben ist oder die Funktion selbst nur indirekt, beispielsweise über Messwerte, zur Verfügung steht. Im Gegensatz dazu wird beim automatischen Differenzieren der Code, der die betrachtete Funktion definiert, um eine Ableitungsfunktion erweitert.

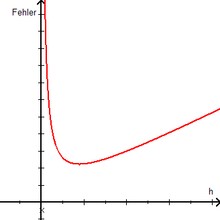
Ist der Abstand (h) der Funktionswerte gering, so wäre bei beliebig genauer Rechnung die Näherung zunächst besser. Allerdings tritt bei der Berechnung mittels Gleitkommazahlen Auslöschung auf, weswegen das gewählte h von der Maschinengenauigkeit abhängige Schranken nicht unterschreiten darf.

Alternativ kann man auch differenzierbare Approximationen von Funktionen wie zum Beispiel kubische Splines verwenden. Ist man nicht am gesamten Funktionsverlauf, sondern nur an einzelnen Stellen interessiert, so existieren spezielle Formeln.

In praktischer Anwendung sind die Funktionswerte oft fehlerbehaftet. Daher werden zum Beispiel zur Kantendetektion Sobel-Operatoren verwendet, die gleichzeitig eine Glättung durchführen. Eine weitere Möglichkeit bietet die Verwendung von geglätteten Splines (auch Ausgleichssplines).

Differenzenquotient

→ Hauptartikel: Differenzenquotient

Ein naheliegender Ansatz ist die Verwendung des Vorwärtsdifferenzenquotienten:

$f'(x) = \frac{f(x+h)-f(x)}{h} + \mathcal O(h)$

Dabei ist jedoch die Näherung im Vergleich zur Auslöschung relativ schlecht. Eine bessere Näherung erhält man durch Verwendung des zentralen Differenzenquotienten:

$f'(x) = \frac{f(x+h)-f(x-h)}{2h} +\mathcal O(h^2)$

Mittels lokaler Polynominterpolation lässt sich diese Näherung noch weiter verbessern. Für die ${\mathcal O}$ -Notation siehe Landau-Symbole.

Numerische Differentiation unter Verwendung komplexer Variable

Ein Problem bei der Anwendung eines klassischen Differenzenquotienten ist die Wahl einer optimalen Schreitweite . Ein zu großes führt zu Rundungsfehlern, während ein zu kleines zu Auslöschung führt. Die numerische Auslöschung infolge der Subtraktion kann durch die komplexwertige Approximation

$f'(x)={\frac {\Im (f(x+\mathrm {i} h))}{h}}+{\mathcal {O}}(h^{2})$

verhindert werden.

Herleitung

Wir betrachten die Taylorreihe von $f(x+h)$ am Entwicklungspunkt

$f(x+h)=f(x)+hf'(x)+{\frac {h^{2}f''(x)}{2}}+{\frac {h^{3}f'''(x)}{6}}+\dots$

Abbruch nach dem linearen Glied und Umstellung nach f'(x) liefert den oben genannten Vorwärtsdifferenzenquotienten. Wir ersetzen nun die reelle Schrittweite durch die imaginäre Schrittweite $\mathrm {i} h$ und erhalten

$f(x+\mathrm {i} h)=f(x)+\mathrm {i} hf'(x)-{\frac {h^{2}f''(x)}{2}}-{\frac {\mathrm {i} h^{3}f'''(x)}{6}}+\dots$

Betrachten wir nun nur den Imaginäranteil dieser Taylorreihe, so erhalten wir

$\Im (f(x+\mathrm {i} h))=hf'(x)-{\frac {h^{3}f'''(x)}{6}}+\dots$

was bei Abbruch nach dem linearen Glied auf die oben angegebene Näherung der Ableitung mit dem Fehler ${\mathcal {O}}(h^{2})$ führt.

Basierend auf einem Artikel in:

Wikipedia.de