Fixpunkt (Mathematik)
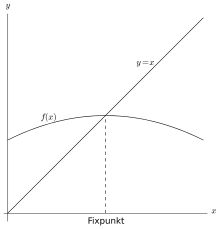
In der Mathematik versteht man unter einem Fixpunkt einen Punkt, der durch eine gegebene Abbildung auf sich abgebildet wird. Die Fixpunkte einer Achsenspiegelung sind die Punkte der Spiegelachse. Eine Punktspiegelung hat nur einen Fixpunkt, nämlich deren Zentrum.
Definition
Sei
eine Menge und
eine Funktion.
Dann heißt ein Punkt
Fixpunkt, falls er die Gleichung
erfüllt.
Anmerkungen
- Ist
eine lineare Abbildung auf dem Vektorraum
, dann nennt man die Fixpunkte von
auch Fixvektoren. Insbesondere sind Fixvektoren also Eigenvektoren von
bezüglich des Eigenwerts 1.
- Da sich jede Gleichung
in eine Fixpunktform mit
umwandeln lässt, sind Fixpunktgleichungen ein Prototyp von nichtlinearen Gleichungen. Ein Wert
ist genau dann Fixpunkt von
wenn dieser Wert auch Lösung der Gleichung
ist.
Fixpunkte in der Numerik
Darüber hinaus gilt folgendes: Der Fixpunkt ist stabil bzw. instabil, wenn ,
der Betrag der Ableitung der betrachteten Funktion, im Schnittpunkt
bzw.
ist. Anschaulich bedeutet dies, dass man die Funktion auf den
Punkt selbst anwenden kann, ohne ihn zu verändern, wobei eine Störung wenig
(bzw. viel) ändert, indem sie zum Fixpunkt hinführt (bzw. vom Fixpunkt
wegführt).
Mit dem Fixpunktproblem verwandt ist das Problem der „iterierten
Abbildungen“, das in der Numerik
und der Chaosforschung
wichtig ist. Mit einem vorgegebenen Anfangswert
beginnend, springt man hier nach dem Schema
treppenartig zwischen der Funktion
und der Diagonale hin und her, und zwar zum Fixpunkt hin oder weg von ihm, je
nachdem ob der Fixpunkt stabil oder instabil ist. Einzelheiten sind u. a. dem
unten angegebenen Buch von H.G. Schuster
zu entnehmen.
Beispiele
- Die Parabelfunktion
, die durch
gegeben ist, hat die zwei Fixpunkte 0 (stabil) und 1 (instabil).
- Sei
ein Vektorraum und
die identische Abbildung, also die Abbildung mit
, dann sind alle
Fixpunkte.
- Sei
der Schwartz-Raum und
die kontinuierliche Fourier-Transformation. Für die Dichtefunktion
der
-dimensionalen Normalverteilung gilt
. Daher ist die Dichtefunktion der Normalverteilung ein Fixpunkt der Fourier-Transformation.
- Das Newton-Verfahren
entspricht der Fixpunktgleichung
.
Raum mit Fixpunkteigenschaft
Definition
Ein topologischer
Raum
besitzt die Fixpunkteigenschaft, falls jede stetige
Abbildung
einen Fixpunkt hat.
Beispiele
- Die Sphäre
besitzt die Fixpunkteigenschaft nicht, denn die Punktspiegelung am Mittelpunkt hat keinen Fixpunkt.
- Eine Vollkugel
hat die Fixpunkteigenschaft. Dies besagt der Fixpunktsatz von Brouwer.
Fixpunktsätze
Die Existenz
von Fixpunkten ist Gegenstand einiger wichtiger mathematischer Sätze. Der Banach'sche
Fixpunktsatz besagt, dass eine Kontraktion
eines vollständigen metrischen
Raumes genau einen Fixpunkt besitzt. Wenn eine Selbstabbildung nur stetig
ist, muss der Fixpunkt nicht eindeutig sein und andere Fixpunktsätze zeigen dann
nur die Existenz. Dabei stellen sie meist stärkere Voraussetzungen an den Raum,
auf dem die Funktion definiert ist. Beispielsweise zeigt der Fixpunktsatz von
Schauder die Existenz eines Fixpunktes in einer kompakten, konvexen
Teilmenge eines Banachraums. Dieser Satz ist eine Verallgemeinerung des Fixpunktsatzes
von Brouwer, der besagt, dass jede stetige Abbildung der abgeschlossenen
Einheitskugel in sich selbst einen Fixpunkt besitzt. Im Gegensatz zu den beiden
anderen Sätzen gilt dieser allerdings nur in endlichdimensionalen Räumen, also
im
oder im
.
Der Fixpunktsatz von Banach liefert außerdem die Konvergenz und
eine Fehlerabschätzung der Fixpunkt-Iteration
im betrachteten Raum. Dieser Satz ergibt somit ein konkretes numerisches
Verfahren zur Berechnung von Fixpunkten.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.02. 2019