Geometrische brownsche Bewegung

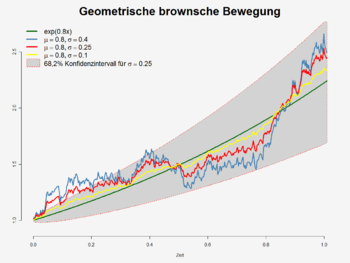
Drei (abhängige) geometrische brownsche Bewegungen mit Drift μ=0,8 und Volatilität σ=0,4 (blau), σ=0,25 (rot) und σ=0,1 (gelb)

Die geometrische brownsche Bewegung ist ein stochastischer Prozess, der sich vom Wiener-Prozess (auch brownsche Bewegung genannt) ableitet. Sie findet vor allem in der Finanzmathematik Verwendung.

Definition

Sei W_t eine Standard-brownsche-Bewegung, d.h. ein Wiener-Prozess. So ist

$S_{t}=a\exp \left[\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}\right]$

eine geometrische brownsche Bewegung.

Herleitung

Drei unabhängige geometrische brownsche Bewegungen mit Volatilität 0,2 und Drift 0,7 (grün), 0,2 (blau) und −0,7 (rot)

Die geometrische brownsche Bewegung ist die Lösung der stochastischen Differentialgleichung

$\mathrm {d} S_{t}=\mu S_{t}\,\mathrm {d} t+\sigma S_{t}\,\mathrm {d} W_{t},\quad t\geq 0,\quad S_{0}=a$

Der Parameter $\mu$ heißt dabei Drift und beschreibt die deterministische Tendenz des Prozesses. Ist $\mu >0$ , so wächst der Wert von in Erwartung, ist er negativ, fällt tendenziell. Für $\mu =0$ ist ein Martingal.

Der Parameter $\sigma$ beschreibt die Volatilität und steuert den Einfluss des Zufalls auf den Prozess . Ist $\sigma =0$ , so verschwindet der Diffusionsterm in der obigen Differentialgleichung, übrig bleibt die gewöhnliche Differentialgleichung

$\mathrm {d} S(t)=\mu \,S(t)\,\mathrm {d} t,\;S(0)=a$ ,

die die Exponentialfunktion $S(t)=ae^{\mu t}$ als Lösung besitzt. Deshalb kann man die geometrische brownsche Bewegung als stochastisches Pendant zur Exponentialfunktion auffassen.

Die stochastische Differentialgleichung der geometrischen brownschen Bewegung kann mit dem Exponentialansatz $S_{t}=e^{X_{t}}$ gelöst werden. Mit Hilfe der Itō-Formel ergibt sich für $X_{t}=\ln(S_{t})$ :

${\begin{aligned}\mathrm {d} X_{t}&=\left(\mu S_{t}{\frac {\partial X_{t}}{\partial S_{t}}}+{\frac {1}{2}}(\sigma S_{t})^{2}{\frac {\partial ^{2}X_{t}}{\partial S_{t}^{2}}}\right)\mathrm {d} t&&+\sigma S_{t}{\frac {\partial X_{t}}{\partial S_{t}}}\mathrm {d} W_{t}\\&=\left(\mu S_{t}{\frac {1}{S_{t}}}-{\frac {1}{2}}(\sigma S_{t})^{2}{\frac {1}{S_{t}^{2}}}\right)\mathrm {d} t&&+\sigma S_{t}{\frac {1}{S_{t}}}\mathrm {d} W_{t}\\&=\left(\mu -{\frac {\sigma ^{2}}{2}}\right)\mathrm {d} t&&+\sigma \mathrm {d} W_{t}\end{aligned}}$

Es ergibt sich also

$\mathrm {d} X_{t}=\left(\mu -{\frac {\sigma ^{2}}{2}}\right)\mathrm {d} t+\sigma \mathrm {d} W_{t}\,,$

und folglich nach Integration

$\ln(S_{t})=\ln(S_{0})+\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}\,.$

Anschließende Exponentiation ergibt die in der Definition angegebene Formel.

Eine andere Möglichkeit, die Lösung zu bestimmen, ist die Verwendung des stochastischen Exponentials: Mit $Z_{t}=\mu t+\sigma W_{t}$ gilt $S_{t}={\mathcal {E}}(Z)_{t}$ .

Eigenschaften

Erwartungswert: für alle $t\geq 0$ gilt: $\mathbb {E} (S_{t})=a\mathrm {e} ^{\mu t}$

Kovarianz: Für alle $s,t\geq 0$ gilt: $\mathrm {Cov} (S_{s},S_{t})=a^{2}\mathrm {e} ^{\mu (t+s)}(\mathrm {e} ^{\sigma ^{2}\min(t,s)}-1)$

Insbesondere gilt also $\mathrm {Var} (S_{t})=a^{2}\mathrm {e} ^{2\mu t}(\mathrm {e} ^{\sigma ^{2}t}-1)$ .

Die geometrische brownsche Bewegung hat unabhängige multiplikative Zuwächse, d.h., für alle $0\leq t_{1}\leq t_{2}\leq \ldots \leq t_{n}$ sind

$S_{t_{1}},{\frac {S_{t_{2}}}{S_{t_{1}}}},\ldots ,{\frac {S_{t_{n}}}{S_{t_{n-1}}}}$ unabhängig.

Verteilungsfunktion: ${\tfrac {S_{t}}{a}}$ ist logarithmisch normalverteilt mit Parametern $(\mu -{\tfrac {1}{2}}\sigma ^{2})t$ und $\sigma ^{2}t$ .

Anwendung

Im Black-Scholes-Modell, dem einfachsten und am weitesten verbreiteten (zeitstetigen) finanzmathematischen Modell zur Bewertung von Optionen, wird die geometrische brownsche Bewegung als Näherung für den Preisprozess eines Basiswertes (zum Beispiel einer Aktie) herangezogen. Dazu führte die vereinfachende Annahme, dass die prozentuale Rendite über disjunkte Zeitintervalle unabhängig und normalverteilt ist. µ spielt hier die Rolle des risikofreien Zinssatzes, σ repräsentiert das Schwankungsrisiko an der Börse. Die oben erwähnte Martingaleigenschaft spielt hier eine zentrale Rolle.

Basierend auf einem Artikel in:

Wikipedia.de