
Satz von Nielsen-Schreier
Der Satz von Nielsen-Schreier ist ein grundlegendes Ergebnis der
kombinatorischen Gruppentheorie,
eines Teilgebiets der Mathematik, das sich mit diskreten (zumeist unendlichen)
Gruppen beschäftigt. Der Satz besagt, dass in einer freien Gruppe jede
Untergruppe frei ist. Neben dieser qualitativen Aussage stellt die quantitative
Fassung eine Beziehung her zwischen dem Index
und dem Rang
einer Untergruppe. Dies hat die überraschende Konsequenz, dass eine freie Gruppe
vom Rang
Untergruppen von jedem beliebigen Rang
und sogar von (abzählbar) unendlichem Rang hat.
Der Satz kann besonders elegant und anschaulich mit Hilfe algebraisch-topologischer Methoden bewiesen werden, mittels Fundamentalgruppe und Überlagerungen von Graphen.
Aussage des Satzes
Ist
eine freie Gruppe, dann ist jede Untergruppe
von
ebenfalls frei.
Hat die Untergruppe endlichen Index, so gilt zusätzlich folgende quantitative Aussage:
Ist
eine freie Gruppe vom Rang
und ist
eine Untergruppe von endlichem Index
,
dann ist
frei vom Rang
.
Dies ist auch für
richtig.
Beweise
Der Satz lässt sich wahlweise mit algebraischen oder topologischen Argumenten beweisen. Ein rein algebraischer Beweis findet sich im unten angegebenen Lehrbuch von Derek John Scott Robinson.[1] Der topologische Beweis gilt als besonders elegant und soll im Folgenden skizziert werden. Er benutzt auf raffinierte Weise die Darstellung freier Gruppen als Fundamentalgruppen von Graphen und ist ein Paradebeispiel für die fruchtbare Wechselwirkung zwischen Algebra und Topologie.
Freie Gruppen als Fundamentalgruppen von Graphen
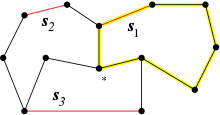
Sei
ein zusammenhängender Graph.
Diesen realisieren wir als topologischen Raum, wobei jede Kante einem Weg zwischen den
angrenzenden Ecken entspricht. Die entscheidende Feststellung ist nun, dass die
Fundamentalgruppe
eine freie Gruppe ist.
Um dieses Ergebnis explizit zu machen und damit auch zu beweisen, wählt man
einen maximalen Baum
,
also einen Baum, der alle Ecken von
enthält. Die verbleibenden Kanten
liefern eine Basis von
,
indem man für jede Kante
einen Weg
wählt, der vom Fußpunkt
im Baum
bis zur Kante
läuft, diese überquert und anschließend in
wieder zum Fußpunkt zurückkehrt. (Man wählt als Fußpunkt zweckmäßigerweise
eine Ecke von
;
diese liegt dann automatisch in jedem maximalen Baum
.)
Die Tatsache, dass die Homotopieklassen
mit
eine Basis von
bilden, kann man mittels kombinatorischer Homotopie beweisen, oder durch
explizite Konstruktion der universellen
Überlagerung des Graphen
.
Dieses Ergebnis können wir quantitativ fassen, wenn
ein endlicher Graph mit
Ecken und
Kanten ist. Er hat dann die Euler-Charakteristik
.
Jeder maximale Baum
enthält dann genau
Ecken und
Kanten, und hat insbesondere die Euler-Charakteristik
.
Es verbleiben die Kanten
und deren Anzahl ist
.
Die Fundamentalgruppe
ist demnach eine freie Gruppe vom Rang
.
Topologischer Beweis des Satzes von Nielsen-Schreier
Qualitative Fassung: Jede freie Gruppe
lässt sich darstellen als Fundamentalgruppe
eines Graphen
.
Zu jeder Untergruppe
gehört eine Überlagerung
.
Der Überlagerungsraum
ist dann wieder ein Graph, also ist die Gruppe
frei.
Quantitative Fassung: Jede freie Gruppe
von endlichem Rang
lässt sich darstellen als Fundamentalgruppe
eines endlichen Graphen
mit Euler-Charakteristik
.
Zu jeder Untergruppe
von Index
gehört dann eine
-blättrige
Überlagerung
.
Der überlagernde Graph
hat also die Euler-Charakteristik
,
und die Gruppe
ist demnach frei vom Rang
.
Folgerungen
Untergruppen der ganzen Zahlen
Für den Rang
ist
die triviale
Gruppe, die nur aus dem neutralen Element besteht, und die Aussage des
Satzes ist leer.
Die erste interessante Aussage finden wir im Rang .
Hier ist
die freie abelsche Gruppe, und wir finden die Klassifikation der Untergruppen
von
wieder: Die triviale Untergruppe
ist frei vom Rang
,
jede andere Untergruppe
ist von der Form
vom Index
und selbst wieder frei abelsch vom Rang
.
Diese einfache Aussage kann auch ohne den Satz von Nielsen-Schreier bewiesen
werden, zeigt aber, was im Spezialfall
in ihm steckt.
Untergruppen nicht-abelscher freier Gruppen
Für eine freie Gruppe
vom Rang
folgt aus dem (quantitativen) Satz von Nielsen-Schreier, dass
freie Untergruppen von beliebigem endlichen Rang enthält. Es genügt, dies für
die von 2 Elementen erzeugte Gruppe
zu zeigen, da diese in allen von
Elementen erzeugten freien Gruppen enthalten ist. Bildet man die beiden Erzeuger
von
auf den Erzeuger der zyklischen Gruppe
ab, so erhält man aus der definierenden Eigenschaft der freien Gruppe einen
surjektiven Gruppenhomomorphismus
.
Nach dem Homomorphiesatz
ist
,
das heißt die Untergruppe
hat den Index
.
Sie ist nach der quantitativen Aussage des Satzes von Nielsen-Schreier daher
isomorph zur von
Elementen erzeugten freien Gruppe.
Man kann in
sogar eine Untergruppe von abzählbar unendlichem Rang konstruieren.
Diese erstaunliche Eigenschaft steht im Gegensatz zu freien abelschen Gruppen (wo der Rang einer Untergruppe stets kleiner oder gleich dem Rang der gesamten Gruppe ist) oder Vektorräumen über einem Körper (wo die Dimension eines Unterraums stets kleiner oder gleich der Dimension des gesamten Raums ist).
Untergruppen endlich erzeugter Gruppen
Der Satz von Nielsen-Schreier handelt zwar zunächst nur von freien Gruppen,
seine quantitative Fassung hat aber auch interessante Konsequenzen für
beliebige, endliche erzeugte Gruppen. Ist eine Gruppe
endlich erzeugt, von einer Familie mit
Elementen aus
,
und ist
eine Untergruppe von endlichem Index
,
dann hat auch
ein endliches Erzeugendensystem
mit höchstens
Elementen.
Wie schon im Fall freier Gruppen muss man im Allgemeinen also damit rechnen,
dass eine Untergruppe
mehr Erzeuger benötigt als die gesamte Gruppe
.
Anmerkungen
- ↑ Derek John Scott Robinson: A Course in the Theory of Groups, Springer-Verlag 1996, ISBN 978-1-4612-6443-9, Satz 6.1.1: The Nielsen-Schreier-Theorem


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.12. 2019