
Kreisschnittebene
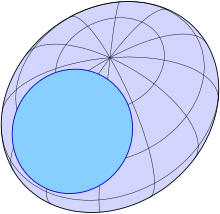
Eine Kreisschnittebene ist in der Geometrie eine Ebene (im 3-dimensionalen Raum), die eine Quadrik (Ellipsoid, Hyperboloid, …) in einem Kreis schneidet. Eine Kugel wird von jeder Ebene, mit der sie wenigstens 2 Punkte gemeinsam hat, in einem Kreis geschnitten. Auch bei Rotationsquadriken (Rotations-Ellipsoid, -Hyperboloid, -Paraboloid, -Zylinder, …) ist die Lage einfach: Sie werden von allen Ebenen, die senkrecht zur Rotationsachse sind, in Kreisen geschnitten, falls sie wenigstens 2 Punkte gemeinsam haben. Nicht mehr offensichtlich ist die Lage bei 3-achsigen Ellipsoiden, echt elliptischen Hyperboloiden, Paraboloiden, Zylindern, …, obwohl es in diesen asymmetrischen Fällen sogar mehr Schnittkreise gibt. Es gilt:
- Jede Quadrik (Fläche im 3-dimensionalen Raum), die Ellipsen enthält, enthält auch Kreise (s. unten).
Quadriken, die nicht dazu gehören, sind: 1) parabolischer Zylinder, 2) hyperbolischer Zylinder und 3) hyperbolisches Paraboloid. Eine umfassende Diskussion aller Fälle ist z.B. in dem Buch von Grotemeyer (s. Literatur) enthalten.
Kreisschnitte von Quadriken wurden früher zur Anfertigung von Modellen verwendet .
Kreisschnittebenen spielen auch in der Kristallographie eine Rolle.
Beschreibung der Methode
Um die Ebenen zu finden, die eine Quadrik in einem Kreis schneiden, werden zwei wesentliche Beobachtungen verwendet:
- (K:) Liegt der Schnitt einer Quadrik mit einer Kugel (Hilfskugel) in einem Ebenenpaar (zwei sich schneidende Ebenen), so besteht der Schnitt aus zwei Kreisen.
- (P:) Schneidet eine Ebene eine Quadrik in einem Kreis, so ist dies auch für alle dazu parallelen Ebenen, die wenigstens zwei Punkte mit der Quadrik gemeinsam haben, der Fall.
Um Kreise auf einer Quadrik zu finden, genügt es also eine Hilfskugel zu finden, die die Quadrik in einem Ebenenpaar schneidet. Dann liefern die zu den Ebenen parallelen Ebenen zwei Scharen von Schnittkreisen.
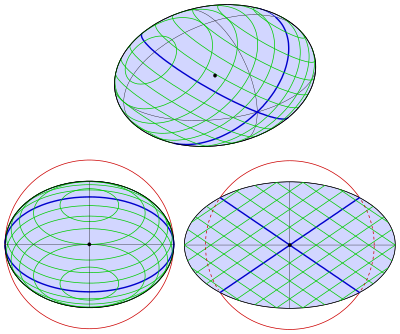
3-achsiges Ellipsoid
Für das Ellipsoid mit der Gleichung
und den Halbachsen
verwendet man eine Hilfskugel mit der Gleichung
Der Kugelradius muss nun so bestimmt werden, dass der Schnitt des Ellipsoids
mit der Kugel in einem Ebenenpaar durch den Ursprung liegt. Damit das
absolute Glied herausfällt, zieht man die Kugelgleichung von dem -Fachen
der Ellipsoidgleichung ab. Es ergibt sich
Diese Gleichung beschreibt nur dann ein Ebenenpaar, wenn einer der drei
Koeffizienten null ist. Sowohl für
als auch für
ergeben sich Gleichungen, die nur von Punkten der
-Achse
bzw.
-Achse
erfüllt werden. Nur der Fall
führt auf ein Ebenenpaar mit der Gleichung
denn nur in diesem Fall haben die verbleibenden Koeffizienten verschiedene
Vorzeichen (wegen ).
Wie die Schnitte mit nicht geeigneten Kugeln aussehen, ist in Abbildung 1 zu erkennen: Radius ist zu groß (magenta) oder zu klein (cyan).
Nähern sich die Werte der Halbachsen
und
an, so nähern sich auch die beiden Scharen von Kreisen an. Für
(Rotationsellipsoid) sind alle Kreisebenen orthogonal zur Rotationsachse.
Nachweis der Eigenschaft (P):
Dreht man das Ellipsoid um die -Achse
so, dass einer der beiden blauen Kreise in der
-Ebene
liegt, so genügt das Ellipsoid einer Gleichung
und für
ergibt sich
.
Damit das eine Kreisgleichung ist, muss
gelten. Schneidet man nun das Ellipsoid mit einer zur
-Ebene
parallelen Ebene mit der Gleichung
,
ergibt sich
.
Diese Gleichung beschreibt einen Kreis oder einen Punkt oder die leere Menge. (Mittelpunkt und Radius ergeben sich nach quadratischer Ergänzung.)
Elliptisches einschaliges Hyperboloid
Für das Hyperboloid mit der Gleichung
erhält man (wie beim Ellipsoid) für den Schnitt mit einer Kugel
die Gleichung
Nur für
ergibt sich hieraus ein Ebenenpaar:
Elliptischer Zylinder
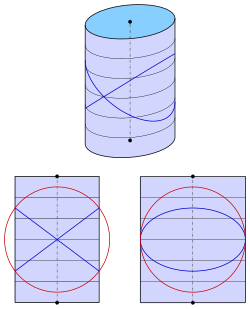
Für den elliptischen Zylinder mit der Gleichung
erhält man die Gleichung
Nur für
ergibt sich ein Ebenenpaar:
Bemerkungen:
- Da aus dem obigen einschaligen Hyperboloid für
der Zylinder dieses Abschnitts wird, ergeben sich auch die Kreisebenen des Zylinders auf diesem Wege aus denen des Hyperboloids.
- Ein elliptischer Zylinder kann also immer auch als schiefer Kreiszylinder aufgefasst werden.
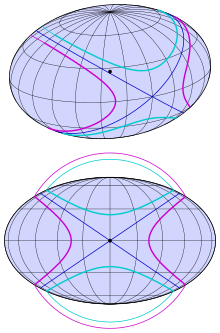
Elliptisches Paraboloid
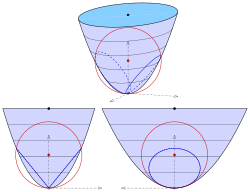
Für das elliptische Paraboloid mit der Gleichung
wählt man eine Kugel durch den Scheitel mit dem Mittelpunkt auf der Achse:
Nach Elimination des linearen Terms ergibt sich die Gleichung
Nur für
ergibt sich ein Ebenenpaar:
Bemerkung:
Der Radius der Kugel ist gleich dem Krümmungskreisradius
der weiteren Parabel
(s. Abbildung 2).
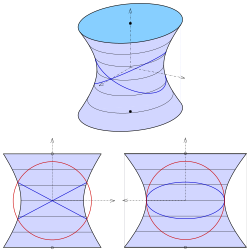
Elliptisches zweischaliges Hyperboloid
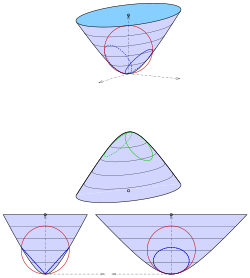
Das zweischalige Hyperboloid mit der Gleichung
verschiebt man zweckmäßigerweise so, dass ein Scheitel der Ursprung ist (s. Abbildung 3):
Die Kugel wählt man auch so, dass sie den Ursprung enthält und ihr
Mittelpunkt auf der -Achse
liegt:
Nach Elimination des linearen Terms ergibt sich die Gleichung
Nur für
ergibt sich ein Ebenenpaar:
Bemerkung:
Der Radius der Kugel ist gleich dem Krümmungskreisradius
der weiteren Hyperbel
(s. Abbildung 3).
Elliptischer Kegel
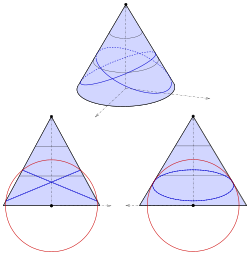
Den elliptischen Kegel mit der Gleichung
verschiebt man zweckmäßigerweise so, dass seine Spitze nicht im Ursprung ist (s. Abbildung 4):
Jetzt kann man eine Kugel um den Ursprung verwenden:
Durch Elimination von
ergibt sich:
Da Ebenen zu erwarten sind, die nicht durch den Ursprung gehen, führt man eine quadratische Ergänzung durch und erhält:
Damit diese Gleichung ein Ebenenpaar beschreibt, muss die rechte Seite null
sein, d.h.
Löst man dann nach
auf, ergibt sich:
Bemerkung:
Ein elliptischer Kegel kann also immer auch als schiefer
Kreiskegel aufgefasst werden. Dabei sollte man aber beachten: Die Gerade
durch die Kegelspitze und den Kreismittelpunkt ist nicht die Kegelachse
(Symmetrieachse).
Literatur
- K. P. Grotemeyer: Analytische Geometrie. Göschen-Verlag, 1962.
- H. Scheid, W. Schwarz: Elemente der Linearen Algebra und der Analysis. Spektrum, Heidelberg, 2009, ISBN 978-3-8274-1971-2.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.12. 2021