Lot (Mathematik)

Lot $\scriptstyle l$ von einem Punkt $\scriptstyle P$ auf eine Gerade $\scriptstyle g$ mit Lotfußpunkt $\scriptstyle L$

Ein Lot ist in der Geometrie eine gerade Linie, die auf einer gegebenen Gerade oder Ebene senkrecht steht. Je nachdem ob es sich bei dieser Linie um eine Gerade oder um eine Strecke handelt spricht man auch von Lotgerade oder Lotstrecke. Der Schnittpunkt des Lots mit der gegebenen Gerade oder Ebene wird Lotfußpunkt genannt. Das Lot kann auf verschiedene Weisen mit Zirkel und Lineal geometrisch konstruiert werden. Berechnet werden kann es durch Ermittlung des Normalenvektors der Gerade oder Ebene oder durch Orthogonalprojektion eines Punkts außerhalb der Gerade oder Ebene. Die Länge der Lotstrecke ist dann gerade der Abstand (Normalabstand) eines Punkts von der Gerade oder Ebene.

Definition

Eine Linie heißt Lot auf eine Gerade oder Ebene , wenn

$l\perp g$ bzw. $l\perp E$

gilt, wenn sie also senkrecht auf der Gerade oder Ebene steht und somit mit ihr einen rechten Winkel bildet. Der Lotfußpunkt ist dann der Schnittpunkt $l\cap g$ bzw. $l\cap E$ des Lots mit der Gerade oder Ebene.

Geometrische Konstruktionen

In zwei Dimensionen lässt sich das Lot auf eine Gerade auf einfache Weise mit Zirkel und Lineal konstruieren. Je nachdem, ob ein gegebener Punkt auf der Geraden oder außerhalb liegt, spricht man vom Errichten oder vom Fällen des Lots.

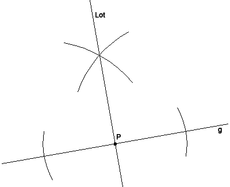
Errichten des Lots

Ist ein Punkt auf der Geraden gegeben, dann findet man die Lotgerade durch diesen Punkt wie folgt: Man sticht den Zirkel in den Punkt ein und bestimmt durch Ziehen eines beliebigen Kreises zwei Punkte auf der Gerade mit gleichem Abstand von . Dann vergrößert man den Winkel des Zirkels, sticht ihn jeweils in einen der beiden gefundenen Punkte auf der Gerade ein und findet durch Ziehen zweier Kreisbögen einen Punkt (von zwei möglichen) außerhalb der Gerade mit gleichem Abstand von den beiden Punkten. Die Gerade, die diesen Punkt gleichen Abstands mit dem Ausgangspunkt verbindet, ist dann die Lotgerade zu durch .

Eine Alternative, auf der Geraden ab dem (oder durch den) Punkt ein Lot zu errichten, ist folgende: Man schlägt um einen frei wählbaren Punkt einen Kreisbogen mit dem Radius $\overline{MP}$ bis er die Gerade in schneidet. Es folgt das Zeichnen einer geraden Linie ab durch bis sie den Kreisbogen in schneidet. Die abschließende gerade Linie, die ab dem (oder durch den) Ausgangspunkt und durch verläuft, ist das Lot auf .


Errichten eines Lots		Errichten eines Lots ( $\scriptstyle M$ frei wählbar) mit Hilfe des Thaleskreises, Animation

Fällen des Lots

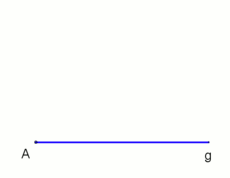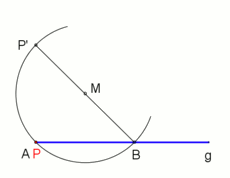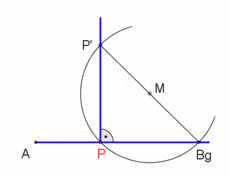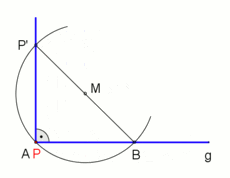
Alternative Methode zum Fällen des Lots

Ist ein Punkt außerhalb der Geraden gegeben, dann findet man das Lot durch diesen Punkt auf die Gerade wie folgt. Man sticht den Zirkel in den Punkt ein und bestimmt durch Ziehen eines Kreises mit entsprechend großem Radius zwei Punkte auf der Gerade mit gleichem Abstand von . Dann verkleinert man gegebenenfalls den Winkel des Zirkels, sticht ihn jeweils in einen der beiden gefundenen Punkte auf der Gerade ein und findet durch Ziehen zweier Kreisbögen einen weiteren Punkt mit gleichem Abstand von den beiden Punkten. Die Gerade, die diesen beiden Punkte gleichen Abstands miteinander verbindet, ist dann die Lotgerade zu durch und der Schnittpunkt dieser Gerade mit ist der Lotfußpunkt.

Eine alternative Konstruktion von einem gegebenen Punkt das Lot auf eine Gerade zu fällen besteht darin, den Zirkel an zwei beliebigen Punkten $M_{1}$ und $M_{2}$ auf der Gerade einzustechen und jeweils den Kreis, der durch den gegebenen Punkt verläuft, einzuzeichnen. Diese beiden Kreise schneiden sich dann in einem weiteren Punkt außerhalb der Gerade und die Verbindungslinie zwischen und ist dann die Lotgerade durch . Diese Konstruktion kann auch für Spiegelungen benutzt werden.

Berechnung

In der analytischen Geometrie werden Punkte in der euklidischen Ebene oder im euklidischen Raum mit Hilfe des kartesischen Koordinatensystems durch Ortsvektoren

$\vec x = (x_1,x_2)$ bzw. $\vec x = (x_1,x_2,x_3)$

beschrieben. Geraden in der Ebene sind typischerweise als Geradengleichung in Parameterform

${\vec r}={\vec r}_{0}+a\,{\vec u}$

gegeben, wobei ${\vec {r}}_{0}$ der Ortsvektor eines Geradenpunkts, ${\vec {u}}$ der Richtungsvektor der Geraden und ein reeller Parameter ist. Ebenen im Raum sind typischerweise als Ebenengleichung in Parameterform

${\vec r}={\vec r}_{0}+a\,{\vec u}+b\,{\vec v}$

gegeben, wobei und reelle Parameter sind, sowie ${\vec {u}}$ und ${\vec {v}}$ die Spannvektoren der Ebene, die nicht kollinear sein dürfen. Zwei Vektoren ${\vec {x}}$ und ${\vec {y}}$ in der Ebene oder im Raum bilden einen rechten Winkel, wenn ihr Skalarprodukt $\vec x \cdot \vec y = 0$ ist.

Errichten des Lots

Der Richtungsvektor der Lotgeraden zu einer gegebenen Gerade oder Ebene ist der Normalenvektor ${\vec {n}}$ der Gerade bzw. Ebene. Man erhält im zweidimensionalen Fall einen Normalenvektor einer Gerade durch Vertauschen der beiden Komponenten ihres Richtungsvektors und durch Umkehrung des Vorzeichens einer der beiden Komponenten über

${\vec n}=(u_{2},-u_{1})$ .

Einen Normalenvektor ${\vec {n}}$ einer Ebene kann man, sofern sie nicht in Normalenform gegeben ist, über das Kreuzprodukt der Spannvektoren durch

${\vec {n}}={\vec {u}}\times {\vec {v}}$

berechnen. Ist nun ein Punkt ${\vec {x}}$ auf der Gerade oder Ebene gegeben, dann ist die Geradengleichung der Lotgerade

${\vec l}={\vec x}+c\,{\vec n}$ ,

wobei eine reelle Zahl ist. Eine Gerade im Raum hat keine ausgezeichnete Normalenrichtung, stattdessen besitzt sie an jedem Geradenpunkt eine Lotebene, deren Normalenvektor gleich dem Richtungsvektor der Geraden ist.

Fällen des Lots

Ist ein Punkt $\vec z$ außerhalb der Gerade oder Ebene gegeben, dann erhält man den Lotfußpunkt ${\vec {y}}$ des Lots von $\vec z$ auf die Gerade oder Ebene als Orthogonalprojektion

${\vec y}={\vec z}-{\frac {({\vec z}-{\vec r}_{0})\cdot {\vec n}}{{\vec n}\cdot {\vec n}}}\,{\vec n}$ .

Es ist auch möglich, das Lot von einem Punkt im Raum auf eine Gerade im Raum zu fällen. Ist ${\vec {u}}$ der Richtungsvektor der Geraden, dann erhält man den Lotfußpunkt ${\vec {y}}$ durch

${\vec y}={\vec r}_{0}+{\frac {({\vec z}-{\vec r}_{0})\cdot {\vec u}}{{\vec u}\cdot {\vec u}}}\,{\vec u}$ .

Der Lotfußpunkt ${\vec {y}}$ ist dann derjenige Geraden- bzw. Ebenenpunkt, dessen Abstand zu $\vec z$ minimal ist. Man definiert damit den Abstand von $\vec z$ zu der Gerade oder Ebene als die Länge der Lotstrecke $|{\vec y}-{\vec z}|$ .

Beispiel

Gegeben sei die Ebene mit dem Fußpunkt ${\vec r}_{0}=(1,0,1)$ und den Spannvektoren $\vec u = ( 2,1,2 )$ und $\vec v = ( 2,-2,-1 )$ . Ein Normalenvektor der Ebene ist dann