Website durchsuchen

Folgereaktion

Die Konzentrationen der in einer Folgereaktion beteiligen Spezies als Funktion der Zeit

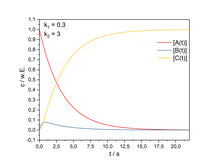
Folgereaktionen, auch Konsekutivreaktionen genannt, sind Reaktionen, in denen Edukte über eine oder mehrere Zwischenstufen in Produkte umgewandelt werden. Die Gesamtreaktion ist daher ein Ergebnis mehrerer aufeinanderfolgender Schritte, dabei hat jede Stufe ihre eigene Geschwindigkeitskonstante. Die wohl einfachste Folgereaktion lautet:

{\displaystyle \mathrm {A{\xrightarrow {k_{1}}}B{\xrightarrow {k_{2}}}C} }

In dieser Reaktion nimmt die Konzentration des Edukts A mit der Zeit ab, während diejenige des Intermediats B zunimmt, ein Maximum durchläuft und schließlich wieder absinkt. Wie groß die maximale Konzentration des Intermediats zu welchem Zeitpunkt sein wird, hängt von den beiden Geschwindigkeitskonstanten {\displaystyle k_{1}} und {\displaystyle k_{2}} ab. Die Bildung des Produkts C beginnt nach Bildung einer bestimmten Menge an Zwischenprodukt (Induktionsperiode).

Geschwindigkeitsgesetze

Es gelten folgende Gleichungen für die Zerfallsgeschwindigkeiten von A und B sowie für die Bildungsgeschwindigkeit von C:

{\displaystyle v_{a}=-{\frac {d\mathrm {[A]} }{dt}}=k_{1}\cdot \mathrm {[A]} }
{\displaystyle v_{b}={\frac {d\mathrm {[B]} }{dt}}=k_{1}\cdot \mathrm {[A]} -k_{2}\cdot \mathrm {[B]} }
{\displaystyle v_{c}={\frac {d\mathrm {[C]} }{dt}}=k_{2}\cdot \mathrm {[B]} }

mit den Geschwindigkeitskonstanten k_{1} der Reaktion {\displaystyle A\rightarrow B} sowie k_{2} der Reaktion B \rightarrow C und der Bedingung:

{\displaystyle {d\mathrm {[A]} }+{d\mathrm {[B]} }+{d\mathrm {[C]} }=0}


Die integrierten Geschwindigkeitsgesetze lauten:

{\displaystyle \mathrm {[A]} _{t}=\mathrm {[A]} _{0}\cdot e^{-k_{1}\cdot t}}
{\displaystyle \mathrm {[B]} _{t}=\mathrm {[A]} _{0}\cdot {\frac {k_{1}}{k_{2}-k_{1}}}\cdot (e^{-k_{1}\cdot t}-e^{-k_{2}\cdot t})}
{\displaystyle \mathrm {[C]} _{t}=\mathrm {[A]} _{0}\cdot (1-{\frac {k_{2}\cdot e^{-k_{1}\cdot t}-k_{1}\cdot e^{-k_{2}\cdot t}}{k_{2}-k_{1}}})}


1. Grenzfall {\displaystyle k_{1}>>k_{2}}:

{\displaystyle \mathrm {[B]} _{t}\approx \mathrm {[A]} _{0}\cdot e^{-k_{2}\cdot t}}
{\displaystyle \mathrm {[C]} _{t}\approx \mathrm {[A]} _{0}\cdot (1-e^{-k_{2}\cdot t})}

Der schnelle erste Reaktionsschritt verschwindet in der Kinetik.


2. Grenzfall {\displaystyle k_{1}<<k_{2}}:

{\displaystyle \mathrm {[B]} _{t}\approx \mathrm {[A]} _{0}\cdot {\frac {k_{1}}{k_{2}}}\cdot e^{-k_{1}\cdot t}}
{\displaystyle \mathrm {[C]} _{t}\approx \mathrm {[A]} _{0}\cdot (1-e^{-k_{1}\cdot t})}

Auch hier verschwindet der schnelle Zwischenschritt aus der Kinetik.


Für beide Grenzfälle gilt immer: Der langsamste Schritt bestimmt in hintereinandergeschalteten Reaktionen den kinetischen Ablauf der Gesamtreaktion.

Siehe auch

Trenner
Basierend auf einem Artikel in: Wikipedia.de
Seitenende
Seite zurück
© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.11. 2022