Lennard-Jones-Potential

Das Lennard-Jones-Potential (nach John Lennard-Jones) beschreibt in der physikalischen Chemie und in der Atom- und Molekülphysik die Bindungsenergie. Es nähert die Wechselwirkung zwischen ungeladenen, nicht chemisch aneinander gebundenen Atomen an.

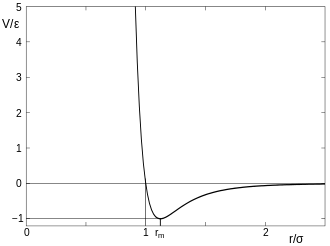
Abbildung 1: Das Lennard-Jones-(12, 6)-Potential , aufgetragen über dem Teilchenabstand .
Im Bereich negativer Steigung wirken abstoßende Kräfte, im Bereich positiver Steigung anziehende.

Beschreibung

Für große Entfernungen zwischen zwei Teilchen überwiegen die anziehenden Kräfte; bei ihnen handelt es sich vor allem um Van-der-Waals-Kräfte, aber auch um permanente Dipol-Dipol-Wechselwirkungen.

Nähert man die jeweiligen Teilchen an, so überwiegt unterhalb eines bestimmten Abstandes $r_{m}\approx 1{,}12\sigma$ (siehe Abbildung 1) der abstoßende Anteil, und die potentielle Energie steigt schnell an. Die abstoßenden Kräfte kommen dadurch zustande, dass die Elektronen bei Annäherung der Atomhüllen teilweise auf energetisch höhere Orbitale ausweichen müssen, weil sie nach dem Pauli-Prinzip nicht zu mehreren den gleichen Zustand besetzen können.

Der anziehende Anteil des Lennard-Jones-Potentials wird abgeleitet aus der London-Formel (Näherung):

$V=-{\frac {C}{r^{6}}}$ ,

wobei

ein relativ komplizierter Term ist, der stoffspezifische Konstanten wie die Ionisierungsenergie für beide betrachteten Teilchen enthält, und
der Abstand zwischen den Teilchen.

Der abstoßende Anteil wird durch eine ähnliche Gleichung beschrieben:

$V={\frac {C_{n}}{r^{n}}}$

Hierbei ist n>6 .

Im Lennard-Jones-(n, 6)-Potential werden die beiden Anteile zusammengefasst:

$V(r)={\frac {C_{n}}{r^{n}}}-{\frac {C}{r^{6}}}$

Aus praktischen Gründen wird oft n = 12 gewählt, weil dann bei der Berechnung der Wert $1/r^{6}$ nur quadriert werden muss. Es entsteht das Lennard-Jones-(12, 6)-Potential, das typischerweise in einer der beiden folgenden Formen geschrieben wird:

${\begin{alignedat}{2}V(r)&=4\varepsilon \left[\left({\frac {\sigma }{r}}\right)^{12}-\left({\frac {\sigma }{r}}\right)^{6}\right]&&=4\varepsilon \cdot \left({\frac {\sigma }{r}}\right)^{6}\cdot \left[\left({\frac {\sigma }{r}}\right)^{6}-1\right]\\&=\varepsilon \left[\left({\frac {r_{m}}{r}}\right)^{12}-2\left({\frac {r_{m}}{r}}\right)^{6}\right]&&=\varepsilon \cdot \left({\frac {r_{m}}{r}}\right)^{6}\cdot \left[\left({\frac {r_{m}}{r}}\right)^{6}-2\right]\end{alignedat}}$

Hierbei ist

$\varepsilon >0$ die „Tiefe“ der Potentialmulde in Einheiten Joule, die durch die beiden Einflüsse entsteht.
$\sigma$ der Teilchenabstand, an dem das Lennard-Jones-Potential eine Nullstelle besitzt: $V(r=\sigma )=0$ .
$r_{m}={\sqrt[{6}]{2}}\cdot \sigma \approx 1{,}12\cdot \sigma$ der Teilchenabstand, in dem das Lennard-Jones-Potential sein Minimum erreicht. In diesem Abstand sind die Kräfte aus dem anziehenden und abstoßenden Anteil des Potentials gleich groß und heben sich auf, so dass in diesem Abstand in Summe keine Kraft zwischen den Teilchen wirkt.

Das Lennard-Jones-Potential ist ein Spezialfall des Mie-Potentials

$V={\frac {C_{n}}{r^{n}}}-{\frac {C_{m}}{r^{m}}}$

das 1903 von Gustav Mie eingeführt wurde.

Sonstiges

Eine weitere Form des Lennard-Jones-Potentials ist das Lennard-Jones-(exp, 6)-Potential, bei dem der abstoßende Term exponentiell ist. Es ist ein Spezialfall des Buckingham-Potentials:

$V(r)={\frac {\varepsilon }{1-6/\alpha }}\cdot \left\langle {\frac {6}{\alpha }}\cdot \exp \left[\alpha \left(1-{\frac {r}{\sigma }}\right)\right]-\left({\frac {\sigma }{r}}\right)^{6}\right\rangle$

mit der „Steilheit“ $\alpha$ als abstoßender Kraft.

Basierend auf einem Artikel in:

Wikipedia.de