Habersche Regel
Die Habersche Regel ist eine in der Toxikologie verwendete mathematische Beziehung zwischen der Konzentration eines Giftstoffes und der Dauer der Verabreichung, beziehungsweise Exposition, dieses Giftes. Die Habersche Regel ist nach dem deutschen Chemiker Fritz Haber benannt, der diese Dosis-Dauer-Beziehung erstmals bei der Einwirkung von Giftgasen, unter anderem Phosgen, aufstellte.
Konzentration × Dauer = konstant
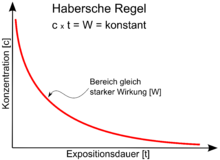
Die Habersche Regel besagt, dass ein konstantes Produkt aus Konzentration (c) und Dauer (t) einer konstanten biologischen Wirkung (k) entspricht:
Die biologische Wirkung kann eine Erkrankung (beispielsweise Krebs) oder der Tod des exponierten Lebewesens sein.
Mit anderen Worten besagt die Habersche Regel, dass identische Produkte von Konzentration und Dauer der Verabreichung dazu führen, dass die gleiche Wirkung eintritt. Das heißt, dass bei ständiger Zufuhr einer unterschwellig toxischen Dosis die Giftigkeit mit der Zeit ansteigt.
Im Diagramm (siehe Abbildung 1) mit linear skalierten Achsen ergibt sich die hyperbolische Kurvenform. In doppeltlogarithmischer Darstellung dagegen eine Gerade.
In der angelsächsischen Fachliteratur sind die Begriffe Haber's Law und Haber's Rule für die Habersche Regel gebräuchlich.
Beispiele
Beispiele für die Gültigkeit und Anwendbarkeit der Haberschen Regel sind das Tabakrauchen mit der Wirkung Lungenkrebs und die Einwirkung ionisierender Strahlungen auf Körpergewebe (Ultraviolettstrahlung → Hautkrebs).
Einschränkungen
Die Habersche Regel ist nur bei irreversiblen Wirkungen von Summationsgiften (auch Kumulationsgifte oder c·t-Gifte genannt) wie beispielsweise Blei, Quecksilber und allen krebserregenden Stoffen anwendbar. Bei lebenswichtigen Spurenelementen, wie beispielsweise Selen oder Zink, versagt die Regel bei niedrigen Konzentrationen völlig. Bei Konzentrationsgiften, wie beispielsweise Kohlendioxid, ist die Habersche Regel ebenfalls nicht anwendbar.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.05. 2025