Griffith-Riss

Der Griffith-Riss ist ein gerader Innenriss, der sich in einer unendlich ausgedehnten Scheibe befindet. Der Griffith-Riss stellt das grundlegende Rissmodell in der Bruchmechanik dar und wurde nach Alan Arnold Griffith benannt. Mit Hilfe dieses Rissmodells hat Griffith grundlegende theoretische Analysen zum Riss und der Rissausbreitung durchgeführt. Der Griffith-Riss findet vor allem in theoretischen Betrachtungen in der linear-elastischen Bruchmechanik Anwendung.

Lastfälle

Scheibe unter Zugbeanspruchung

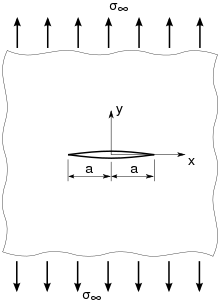
Griffith-Riss unter Zugbeanspruchung.

Für einen Riss der Länge 2a in einer Scheibe unter der Zugspannung $\sigma _{\infty }$ (Spannung senkrecht zur Rissebene) bestimmte Griffith die Energiefreisetzungrate

$G={\frac {2\pi \sigma _{\infty }^{2}a}{E'}}=4\gamma$

mit $E'=\left\{{\begin{array}{ll}E&{\text{: ebener Spannungszustand (ESZ)}}\\\displaystyle {\frac {E}{(1-\nu )^{2}}}&{\text{: ebener Verzerrungszustand (EVZ).}}\end{array}}\right.$

Hierbei ist:

der Elastizitätsmodul
$\nu$ die Querkontraktionszahl
$\gamma$ die spezifische Oberflächenenergie

Der Spannungsintensitätsfaktor für den Rissöffnungsmodus I berechnet sich zu

$K_{\mathrm {I} }=\sigma _{\infty }\cdot {\sqrt {\pi \cdot a}}$ .

Scheibe unter Schubbeanspruchung

Griffith-Riss unter Schubbeanspruchung.

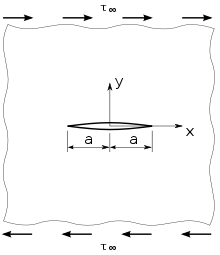
Der Spannungsintensitätsfaktor für den Rissöffnungsmodus II unter der Schubbeanspruchung $\tau _{\infty }$ berechnet sich zu

$K_{\mathrm {II} }=\tau _{\infty }\cdot {\sqrt {\pi \cdot a}}$ .

Bedeutung

Vergleicht man die obigen K-Faktoren für den Modus I und II mit der allgemeinen Gleichung für den Spannungsintensitätsfaktor für Risse in Bauteilen

$\left\{{\begin{matrix}K_{\mathrm {I} }\\K_{\mathrm {II} }\end{matrix}}\right\}=\left\{{\begin{matrix}\sigma \\\tau \end{matrix}}\right\}\cdot {\sqrt {\pi \cdot a}}\cdot \left\{{\begin{matrix}Y_{\mathrm {I} }\\Y_{\mathrm {II} }\end{matrix}}\right\}$ ,

so erkennt man, dass für den Griffith-Riss die Geometriefaktoren $Y_{\mathrm {I} }=1$ und $Y_{\mathrm {II} }=1$ sind. Somit lassen sich die Spannungsintensitätsfaktoren $K_{\mathrm {I} }$ und $K_{\mathrm {II} }$ für Risse in beliebigen Bauteilen auf die Spannungsintensitätsfaktoren des Griffith-Risses normieren.

Siehe auch

Airysche Spannungsfunktion#Der Griffith Riss: Spannungsfeld um den Riss in der linearen ebenen Elastostatik.

Literatur

D. Gross, Th. Seelig: Bruchmechanik mit einer Einführung in die Mikromechanik. 5. Aufl., Springer, Berlin 2011, ISBN 978-3-642-10196-0.
Kuna, M.: Numerische Beanspruchungsanalyse von Rissen – Finite Elemente in der Bruchmechanik. 2. Aufl., Vieweg+Teubner 2010, ISBN 978-3-8348-1006-9.

Basierend auf einem Artikel in:

Wikipedia.de