Coulombwall

Coulombwall

Als Coulombwall oder Coulombbarriere wird das Potential bezeichnet, gegen das ein positiv geladenes Teilchen anlaufen muss, um in den ebenfalls positiv geladenen Atomkern zu gelangen. Dieses Potential beruht auf der Coulombkraft (benannt nach Charles Augustin de Coulomb), die zwischen zwei elektrischen Ladungen mit gleichem Vorzeichen abstoßend wirkt.

Zur Überwindung der Barriere benötigt das Teilchen nach der klassischen Mechanik eine Mindestenergie. Nach der Quantenmechanik besteht dagegen auch bei geringerer Teilchenenergie eine gewisse Chance zur Durchtunnelung einer solchen Barriere.

Ernest Rutherford beobachtete als Erster, dass Alphastrahlung – die aus positiv geladenen Teilchen besteht – die Barriere von Atomkernen überwinden und so Kernreaktionen auslösen kann. Solche Experimente gaben erste Hinweise auf Bestandteile und Aufbau der Atomkerne.

Zur Entdeckung der Quarks und Postulierung der Gluonen war die Überwindung der Coulombbarriere des Protons notwendig.

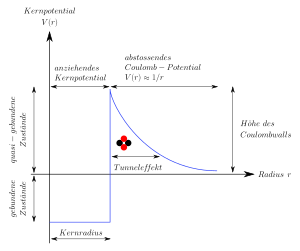
Das Potential im Atomkern und in seiner Nähe wird durch die elektromagnetische und die „starke“ Wechselwirkung bestimmt. Die langreichweitige elektromagnetische Wechselwirkung bewirkt (hier in Form der erwähnten Coulombkraft) ein abstoßendes Potential bei großen Abständen. Bei kleinen Abständen dagegen sorgt die kurzreichweitige starke Wechselwirkung für ein anziehendes Kernpotential und bestimmt so die Größenordnung des Atomkerns. Die Summierung beider Effekte ergibt ein bindendes oder quasibindendes Potential.

Die Potentialbarriere mit ihrer endlichen Höhe wird als „Coulomb“wall bezeichnet, obwohl sie erst durch das Zusammenwirken der beiden verschiedenen Grundkräfte zustande kommt. Ihre effektive Höhe hängt neben der Ladung des Atomkerns und der Ladung des einlaufenden Teilchens auch vom Drehimpuls des einlaufenden Teilchens ab.

Die endliche Höhe des Coulombwalls erklärt auch den Alphazerfall mancher Atomkerne und spielt bei vielen Kernreaktionen eine Rolle, denn ein geladenes Teilchen muss auch beim Verlassen des Kerns die Barriere entweder überwinden oder „durchtunneln“.

Berechnung

Die Höhe des Coulombwalls beträgt:

$V_{c}={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Z_{1}\,Z_{2}\,e^{2}}{r}}$

Näherungsweise lässt sie sich in MeV mit folgender Faustformel bestimmen:

$V_{C}\approx {\frac {Z_{1}\cdot Z_{2}}{A^{\frac {1}{3}}}}$

Darin sind $Z_{1}$ und $Z_{2}$ die Kernladungszahlen von Projektil und Targetkern sowie die Massenzahl des Targetkerns.

Trivia

Die Straße „Am Coulombwall“ in Garching bei München wurde nach dem Coulombwall benannt.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de