Binäres Entscheidungsdiagramm

Ein binäres Entscheidungsdiagramm (BED; engl. binary decision diagram, BDD) ist eine Datenstruktur zur Repräsentation Boolescher Funktionen. Binäre Entscheidungsdiagramme werden vor allem im Bereich der Hardwaresynthese und -verifikation eingesetzt.

Ein BED kann als eine Art Flussdiagramm zur Auswertung einer Booleschen Funktion $f(x_{1},\ldots ,x_{n})$ verstanden werden. Dabei wird nacheinander der Wert der Variablen $x_{1}$ , $x_{2}$ , ... abgefragt, mit den zwei Entscheidungsmöglichkeiten Wahr oder Falsch, welche jeweils in unterschiedliche Teilbereiche des Diagramms verzweigen. Als Ergebnis erhält man schließlich den Wert der Booleschen Funktion unter der gewählten Variablenbelegung. Die Darstellung des Diagramms ist dabei weitestgehend komprimiert, so dass für das Ergebnis irrelevante Fragen ausgelassen und doppelte Teildiagramme zusammengelegt werden.

Definition

Ein binäres Entscheidungsdiagramm ist ein azyklischer, gerichteter Graph G=(V,E) mit einer Wurzel, so dass gilt

Jeder Knoten aus ist entweder ein Blatt oder ein innerer Knoten.
Blätter besitzen keine ausgehenden Kanten und sind mit einem Wert aus $\{0,1\}$ beschriftet.
Jeder innere Knoten besitzt genau zwei ausgehende Kanten, die als niedrig- bzw. hoch-Kante bezeichnet werden. Die Endpunkte dieser Kanten werden mit $\operatorname {niedrig} (v)$ bzw. $\operatorname {hoch} (v)$ bezeichnet. Außerdem ist jeder innere Knoten mit einer Variablen $x_{i}$ beschriftet.

Solch ein BED heißt geordnet (Variablenordnung, OBDD), falls die Variablen auf allen von der Wurzel ausgehenden Pfaden in derselben Reihenfolge auftauchen.

Ein BED heißt reduziert (RBDD), falls die folgenden zwei Operationen erschöpfend angewendet wurden:

Je zwei isomorphe Teilgraphen werden zu einem verschmolzen
Elimination ("Überbrückung") von Knoten, dessen zwei Endpunkte identisch sind

Der Begriff binäres Entscheidungsdiagramm, schließt dabei im Allgemeinen bereits die Forderungen nach Variablenordung und Reduktion mit ein. Der Vorteil dieser Eigenschaften ist, dass für jede Boolesche Funktion (bei fester Variablenordnung) genau ein reduziertes geordnetes BED existiert, d.h. es ist eine kanonische Darstellung der Booleschen Funktion (Bryant, 1986).

Durch die Shannon-Zerlegung kann die von einem binären Entscheidungsdiagramm dargestellte Boolesche Funktion berechnet werden. Sei aus ein Knoten des binären Entscheidungsdiagramms. Dann ist die von dargestellte Funktion $f_{v}$ definiert als

falls ein Blatt ist, dann ist die dargestellte Funktion $f_{v}$ der Wert der Beschriftung von
falls ein innerer Knoten mit Beschriftung $x_{i}$ ist, dann ist $f_{v}(x)=x_{i}f_{\operatorname {hoch} (v)}(x)\vee {\overline {x_{i}}}f_{\operatorname {niedrig} (v)}(x)$ .

Beispiel

Darstellung eines BDDs

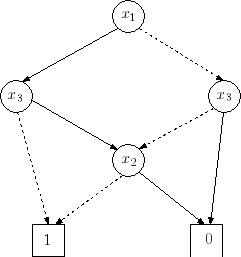
Dieses Bild stellt ein freies, geordnetes und reduziertes binäres Entscheidungsdiagramm dar. Dabei wird die niedrig-Kante eines Knotens gestrichelt und die hoch-Kante durchgezogen dargestellt. Die verwendete Variablenordnung ist $x_{1}<x_{3}<x_{2}$ . Die dargestellte Funktion lässt sich folgendermaßen berechnen:

$x_{2}$ -Knoten:

$f_{1}(x_{1},x_{2},x_{3})=0\cdot x_{2}\vee 1\cdot {\overline {x_{2}}}={\overline {x_{2}}}$

linker $x_{3}$ -Knoten:

$f_{2}(x_{1},x_{2},x_{3})=f_{1}\cdot x_{3}\vee 1\cdot {\overline {x_{3}}}={\overline {x_{2}}}x_{3}\vee {\overline {x_{3}}}$

rechter $x_{3}$ -Knoten:

$f_{3}(x_{1},x_{2},x_{3})=0\cdot x_{3}\vee f_{1}\cdot {\overline {x_{3}}}={\overline {x_{2}}}\,{\overline {x_{3}}}$

$x_{1}$ -Knoten:

$f_{4}(x_{1},x_{2},x_{3})=f_{2}\cdot x_{1}\vee f_{3}\cdot {\overline {x_{1}}}=x_{1}{\overline {x_{2}}}x_{3}\vee x_{1}{\overline {x_{3}}}\vee {\overline {x_{1}}}\,{\overline {x_{2}}}\,{\overline {x_{3}}}$

Wir können die dargestellte Funktion auch direkt für eine gegebene Variablenbelegung auswerten. Dazu muss lediglich dem Pfad, der zu der Belegung gehört, gefolgt werden, bis man ein Blatt erreicht. Der Wert dieses Blattes ist der Funktionswert für die gegebene Variablenbelegung.

Nehmen wir an, wir wollen für obiges Beispiel den Funktionswert für $(x_{1},x_{2},x_{3})=(0,1,1)$ bestimmen. Wir beginnen an der Wurzel des binären Entscheidungsdiagramms. Dieser Knoten ist mit $x_{1}$ beschriftet. Da in unserer Belegung $x_{1}=0$ ist, folgen wir der niedrig-Kante und erreichen einen Knoten, der mit $x_{3}$ beschriftet ist. Es gilt $x_{3}=1$ , also folgen wir der hoch-Kante und erreichen das Blatt mit der Beschriftung 0. Folglich gilt f(0,1,1)=0 .

Variablenordnungen

Die Struktur und die Zahl der Knoten eines geordneten und reduzierten binären Entscheidungsdiagramms hängen bei vielen Funktionen stark von der gewählten Variablenordnung ab. Als Beispiel betrachten wir die Boolesche Funktion $f(x_{1},\ldots ,x_{2n})=x_{1}x_{2}\vee x_{3}x_{4}\vee \dots \vee x_{2n-1}x_{2n}$ . Wählt man dafür die Variablenordnung $x_{1}<x_{3}<\dots <x_{{2n-1}}<x_{2}<x_{4}<\dots <x_{{2n}}$ , so benötigt das binäre Entscheidungsdiagramm mehr als $2^{n}$ Knoten. Bei der Variablenordnung $x_{1}<x_{2}<x_{3}<x_{4}<\dots <x_{{2n-1}}<x_{{2n}}$ genügen hingegen Knoten.

Binäres Entscheidungsdiagramm für die Funktion $f(x_{1},...,x_{8})=$
$x_{1}x_{2}\vee x_{3}x_{4}\vee x_{5}x_{6}\vee x_{7}x_{8}$ mit schlechter Variablenordnung

Gute Variablenordnung

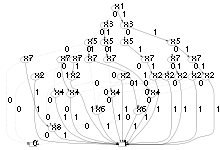
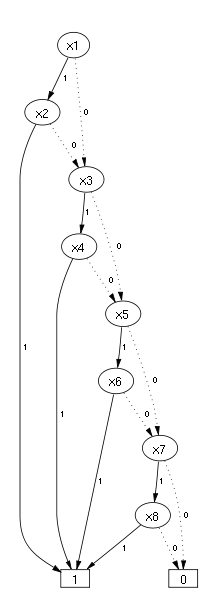
Es gibt auch Funktionen, die unabhängig von der Variablenordnung exponentiell in Zahl der Variablen viele Knoten benötigen. Dazu gehören auch so wichtige Funktionen wie die Multiplikation. Deshalb wurden im Laufe der Jahre zahlreiche Varianten von binären Entscheidungsdiagrammen entwickelt, wie beispielsweise Kronecker Functional Decision Diagrams, Binary Moment Diagrams, Edge-valued Binary Decision Diagrams und zahlreiche andere.

Operationen auf binären Entscheidungsdiagrammen

Die Operationen, die normalerweise von allen Implementierungen zur Verfügung gestellt werden, sind zumindest die Booleschen Verknüpfungen Konjunktion (AND), Disjunktion (OR) und die Negation (NOT).

Die Negation kann durchgeführt werden, indem man das 0- und das 1-Blatt des binären Entscheidungsdiagramms vertauscht. Die übrigen zweistelligen Booleschen Operationen werden normalerweise auf einen speziellen ternären Operator, den sogenannten ITE-Operator zurückgeführt:

$\operatorname {ITE} (f,g,h)=(f\wedge g)\vee (\neg f\wedge h)$

Der Name ITE kommt von if-then-else: Wenn das Argument gleich 1 ist, dann ist der Funktionswert von ITE gleich dem Funktionswert von , ansonsten gleich dem von .

Mit Hilfe von ITE können wir schreiben:

$f\wedge g=\operatorname {ITE} (f,g,0)$

$f\vee g=\operatorname {ITE} (f,1,g)$

$\neg f=\operatorname {ITE} (f,0,1)$

Man kann sich leicht davon überzeugen, dass sich alle 16 binären Booleschen Operationen mit Hilfe des ITE-Operators ausdrücken lassen. Es genügt folglich, eine Implementierung des ITE-Operators anzugeben.

Weitere wichtige Operationen sind beispielsweise:

Test von zwei dargestellten Funktionen auf Gleichheit. Die meisten verfügbaren Implementierungen sorgen dafür, dass Knoten, die dieselbe Funktion darstellen, nur einmal angelegt werden. Dann können einfach die Zeiger auf die Knoten der binären Entscheidungsdiagramms verglichen werden: sind sie gleich, so auch die dargestellten Funktionen und umgekehrt. Damit ist die Laufzeit konstant (d. h. ).
Test auf Erfüllbarkeit der dargestellten Funktion, also Beantwortung der Frage, ob es eine Belegung der Variablen gibt, so dass die Funktion den Wert 1 annimmt. Dazu muss das binäre Entscheidungsdiagramm lediglich mit dem 0-Blatt verglichen werden.
Berechnung der Anzahl der erfüllenden Belegungen: kann durch Traversieren des binären Entscheidungsdiagramms in Linearzeit geschehen. Für Details siehe [1].

Implementierungen

CMU BDD, BDD-Paket, Carnegie Mellon University, Pittsburgh
CUDD: BDD-Paket, University of Colorado, Boulder
CrocoPat: BDD-Paket mit Interpreter für Relationales Programmieren, University of California, Berkeley
JINC: Eine parallele (multi-threading) C++ Bibliothek, Universität Bonn.
BuDDy : libbdd, eine sehr effiziente BDD Library, geschrieben in C, mit C++ Interface

Literatur

Rolf Drechsler, Bernd Becker: Graphenbasierte Funktionsdarstellung. Boolesche und Pseudo-Boolesche Funktionen, Teubner Verlag 1998, ISBN 3-519-02149-8
Donald E. Knuth: The Art of Computer Programming - Combinatorial Algorithms, Part 1, Addison-Wesley 2011, 202–280, ISBN 0-201-03804-8

Basierend auf einem Artikel in:

Wikipedia.de