Fresnelsches Parallelepiped

Das Fresnelsche Parallelepiped (auch: Fresnelsches Rhomboeder) ist ein optisches Prisma das 1817 von Augustin-Jean Fresnel vorgestellt wurde, um 45°-linear-polarisiertes Licht in zirkular-polarisiertes Licht umzuwandeln. Die Funktion des Parallelepipeds ist daher ähnlich der einer Verzögerungsplatte, jedoch basiert es nicht auf der Erzeugung einer definierten Phasenverschiebung durch Doppelbrechung sondern aufgrund einer zweifachen Totalreflexion in einem bestimmten Winkel. Es hat den Vorteil, dass die Phasenverschiebung im Gegensatz zu $\Delta n$ bei der Verzögerungsplatte kaum von der Wellenlänge abhängt.

Aufbau und Funktionsweise

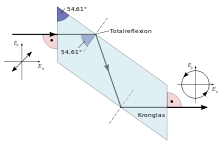
Strahlengang in einem Fresnelschen Parallelepiped

Die Funktion des Fresnelschen Parallelepipeds basiert auf einer definierten Phasenverschiebung der beiden Komponenten des polarisierten Lichts bei der Totalreflexion an der Innenfläche des Prismas. Dazu wird 45°-linear-polarisiertes Licht senkrecht auf eine Stirnseite des Prismas gelenkt und ohne Richtungsänderung in das Prisma gebrochen. Anschließend fällt es auf eine schräge Längsfläche des Prismas. Ist der Einfallswinkel 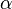$\alpha$ größer als der Grenzwinkel der Totalreflexion $\alpha_\text{krit}$ , wird es dort totalreflektiert. Die dabei auftretende Phasenverschiebung bewirkt, dass aus dem ursprünglich linear-polarisiertem Licht elliptisch-polarisiertes Licht wird. Für die Erzeugung von zirkular-polarisiertem Licht ist daher noch eine zweite Totalreflexion notwendig, bevor das Licht durch die zweite Stirnseite des Prismas austritt.

Wie bereits erwähnt, ist es für eine definierte Phasenverschiebung von $\delta = 90^\circ$ notwendig, dass das Licht in einem bestimmten Winkel auf die totalreflektierenden Grenzflächen trifft. Der Winkel ist abhängig von dem Brechungsindex des eingesetzten Materials und lässt sich aus folgender Beziehung berechnen:

$\tan \frac{\delta}{2n} = \frac{\cos\alpha \sqrt{\sin^2\alpha-\sin^2\alpha_\text{krit}}}{\sin^2\alpha}$

wobei 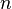die Anzahl der Totalreflexionen im Parallelepiped ist. Der Brechungsindex des Materials fließt in $\alpha_\mathrm{krit}$ ein.

Normalerweise erfolgen bei einem Fresnelschen Parallelepiped zwei Totalreflexionen im Prisma. Für ein Prisma aus Kronglas mit einem Brechungsindex von 1,51 muss der Einfallswinkel auf die totalreflektierenden Flächen daher rund 54,62° betragen.

Basierend auf Artikeln in:

Wikipedia.de