Monochromatische Aberration

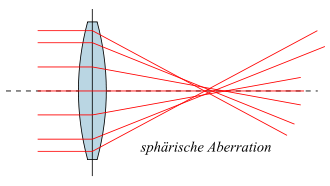
Sphärische Aberration

Sphärische Aberration zweiter (niedrigster) Ordnung

Auf der Abbildung erkennt man, wie die roten einfallenden Strahlen an einem sphärischen Hohlspiegel reflektiert werden. Den durch die grünen Strahlen erkennbaren Abbildungsfehler nennt man Katakaustik.

Die sphärische Aberration, auch Öffnungsfehler oder Kugelgestaltsfehler genannt, ist ein Schärfefehler und bewirkt, dass achsparallel einfallende oder vom gleichen Objektpunkt auf der optischen Achse ausgehende Lichtstrahlen nach dem Durchgang durch das System nicht die gleiche Schnittweite haben. Sie laufen somit nicht in einem Punkt zusammen. Im Allgemeinen ist die Abweichung umso stärker, je weiter außen der Strahl verläuft. Die Schnittweite des gebrochenen Strahls wird aus Symmetriegründen durch eine gerade Funktion gegeben:

$s=s_{0}+\sum _{{k=1}}^{{\infty }}w_{{2k}}a^{{2k}}$

Dabei ist der Achsabstand, mit dem der Strahl in das System einfällt, und w_k gibt die Stärke der sphärischen Aberration k-ter Ordnung an. $s_{0}$ ist die paraxiale Schnittweite des gebrochenen Strahls.

Objektive mit sphärischer Aberration liefern ein weiches Bild mit zwar scharfen, aber kontrastarmen Details, zu denen nur die achsnahen Strahlen beitragen. Die achsfernen Strahlen erzeugen Halos an Hell-Dunkel-Übergängen.

Motive vor und hinter der Ebene maximaler Schärfe werden unterschiedlich unscharf gezeichnet. Es gibt Objektive, deren sphärische Aberration man stufenlos in einem weiten Bereich einstellen kann, um die Unschärfe vor und hinter dem Fokus und die Schärfe im Fokus anpassen zu können.

Mit einem System, das nur sphärische (kugelförmige) brechende oder reflektierende Flächen enthält, kann man keine von sphärischer Aberration völlig freie reelle Abbildung erreichen. Mit einer asphärischen Oberfläche einer Linse oder eines Spiegels kann man die sphärische Aberration völlig korrigieren. Allerdings ist das Schleifen einer Kugeloberfläche deutlich einfacher und damit billiger als das Schleifen asphärisch gekrümmter Flächen. Der weite Einsatz sphärischer Flächen beruht auf der Tatsache, dass ihre Abbildungseigenschaften gut genug sind, bei gleichzeitig akzeptablem Herstellungsaufwand. Die Kosten für asphärisch geschliffene Linsen relativieren sich bei Mehrlinsensystemen, da man gegebenenfalls mit weniger Linsen die gleiche Abbildungsgüte erzielen kann.

Unterdessen gibt es Verfahren, Asphären hoher Qualität als Presslinge (Molding) herzustellen. Es gibt zwei Herstellungsverfahren: Kleine Linsen können direkt gepresst werden; größere werden durch Umformen einer volumengleichen sphärischen Linse hergestellt. Die Größe ist dabei nach oben durch zwei Probleme beschränkt: Zum einen gibt es nur wenige Glassorten, die für eine Umformung geeignet sind, zum anderen neigen umgeformte Linsen zu Inhomogenitäten durch innere Spannungen, die durch den Umformprozess entstehen.

Kleine Kunststofflinsen werden im Spritzgieß- oder Spritzprägeverfahren kostengünstig gefertigt.

In einigen Fällen wird auch eine Kunststoffschicht auf eine sphärische Glaslinse gegossen und dann durch Pressen in eine asphärische Form gebracht.

Mit Hilfe des foucaultschen Schneidenverfahrens lassen sich sphärische Aberrationen auch mit einfachen Mitteln gut nachweisen. In der Massenfertigung optischer Teile sind heute interferometrische Verfahren üblich.

Sofern die sphärische Aberration das Auflösungsvermögen begrenzt, kann dieses durch Abblenden bis zur kritischen Blende gesteigert werden.

Bei der Reflexion an einem sphärischen Hohlspiegel entsteht ein Abbildungsfehler, dieser trägt den Namen Katakaustik.

Astigmatismus schiefer Bündel

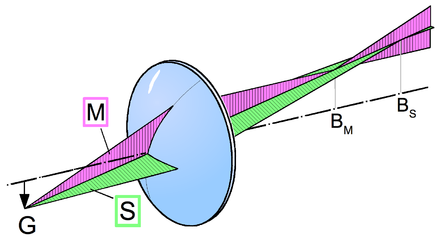
Astigmatismus: Objekte, die außerhalb der optischen Achse liegen, werden unscharf abgebildet. Ursache sind die verschiedenen Brennweiten in der Meridional- (M) und Sagittalebene (S).

Astigmatismus ist ein Schärfefehler, welcher das von einem Objektpunkt ausgehende und schräg in das Objektiv einfallende Strahlenbündel betrifft. Dabei ist zwischen Meridional- und Sagittalebene zu unterscheiden. In Richtung der Meridionalebene (M), welche die optische Achse enthält, ist die Linse perspektivisch verkürzt, die Einfallswinkel variieren schneller mit dem Versatz des Strahls im Bündel. Daraus resultiert eine kürzere Brennweite.

Hinzu kommt, dass in den Punkten (B_M und B_S) keine Punkte, sondern Brennlinien in der jeweils anderen Ebene abgebildet werden. Somit entsteht vor und hinter den beiden Brennebenen statt eines Kreises ein Oval, da jedes Strahlenbündel einer Ebene zur Ellipse wird und in jedem Punkt einen anderen Öffnungswinkel hat. Wird ein Schirm hinter die sagittale Brennebene gehalten, ist ein Oval mit langer Halbachse in meridonaler Richtung (rot) zu sehen. Analog dazu ist das Oval vor der meridionalen Brennebene mit längerer Halbachse in sagittaler Richtung (grün). Dazwischen existiert eine Stelle, wo ein Punkt als unscharfer Kreis abgebildet wird, der kleinste Zerstreuungskreis oder Kreis kleinster Verwirrung.

Charakterisiert wird der Astigmatismus durch die astigmatische Differenz, den Abstand zwischen den Brennlinien. Dieser wächst mit stärkerer Neigung des einfallenden Bündels zur optischen Achse, der Linsenstärke, der Linsendicke und der Linsengeometrie. So haben Bi-Linsen im Gegensatz zu durchgebogenen Linsenformen einen besonders starken Astigmatismus bei schräg einfallendem Einfallsbündel. Dieser Linsenfehler wurde im Mittelalter und früher Neuzeit zur Korrektur des Augenastigmatismus benutzt, indem man schräg durch die Bi-Brille durchsah und dadurch seinen eigenen Astigmatismus kompensierte. Typisch ist der dadurch entstehende Schneiderblick oder Schneiderhals.

Ein optisches System kann so konstruiert werden, dass Astigmatismus-Effekte verringert oder verhindert werden. Solche Optiken heißen Anastigmaten. Diese Bezeichnung hat nur noch historische Bedeutung, da dieser Fehler bei modernen Objektiven nur mehr bei schweren Fabrikationsfehlern auftritt. Eine Ausnahme stellen die Schiefspiegler – eine Gruppe von astronomischen Teleskopen – dar, bei denen der Fehler besonders korrigiert wird.

Ein dem Astigmatismus ähnlicher Bildfehler kann bei Spiegelteleskopen der Amateurastronomie auftreten, deren Fokussierung oft durch axiale Verschiebung des Hauptspiegels erfolgt. Dies kann zu kleinen Verkippungen führen, wodurch das Bild der Sterne nicht mehr punktförmig ist, sondern bei Scharfstellung von extra- bzw. intrafokaler Seite horizontal bzw. vertikal etwas länglich erscheint.

Axialer Astigmatismus

Unvollkommene Linsen, die nicht korrekt rotationssymmetrisch um die optische Achse sind, bilden auch achsparallele Bündel astigmatisch ab. Ein Objektpunkt wird je nach Fokussierung als Strich (längs oder quer) abgebildet. Dieser Fehler spielt in der Augenoptik und der Elektronenoptik eine entscheidende Rolle. Die einfachste Form des axialen Astigmatismus lässt sich durch Kombination mit einer in Brechkraft und Achsrichtung genau dimensionierten Zylinderlinse korrigieren (Zylinderglas in der Brille, Stigmator im Elektronenmikroskop). Die Fertigung von Glaslinsen für sichtbares Licht ist inzwischen so vollkommen, dass hier kein störender axialer Astigmatismus auftritt.

Koma

Die Koma (Asymmetriefehler, von lat. coma ‚Schopf, Schweif‘) entsteht bei schräg zur optischen Achse einfallendem Strahlenbündel durch eine Überlagerung zweier Abbildungsfehler: der auch bei achsparallelem Bündel wirkenden sphärischen Aberration und dem Astigmatismus schiefer Bündel. Anstelle eines scharfen Beugungsscheibchens entsteht ein Bildpunkt mit zum Rand der Optik gerichtetem „Schweif“, der dem Phänomen den Namen gibt. Durch Abblenden der Randstrahlen kann die Erscheinung gemindert werden, der Astigmatismus schiefer Bündel bleibt aber bestehen.

Koma kann sowohl bei Linsen als auch bei Spiegeloptiken auftreten. Optische Systeme bei denen sowohl die sphärische Aberration als auch die Koma vollständig korrigiert sind, heißen Aplanate.

Verzeichnung

Geometrische Verzeichnung

→ Hauptartikel: Verzeichnung

Verzeichnung ist ein Lagefehler und bedeutet, dass die Bildhöhe (Abstand eines Bildpunkts von der Bildmitte) auf nichtlineare Weise von der Höhe des entsprechenden Objektpunkts abhängt. Man kann auch sagen: Der Abbildungsmaßstab hängt von der Höhe des Objektpunkts ab. Man beachte, dass hier der Begriff „Bildmitte“ nicht den rechnerischen Mittelpunkt des Bildes bezeichnet, der sich durch die Pixelzahl ergibt. Vielmehr ist der Punkt gemeint, in dem die optische Achse die Bildebene schneidet. Dieser Punkt wird auch als Verzeichnungszentrum bezeichnet.

Verzeichnung bewirkt, dass gerade Linien, deren Abbild nicht durch die Bildmitte geht, gekrümmt wiedergegeben werden.

Wenn der Abbildungsmaßstab mit zunehmender Höhe abnimmt, nennt man dies tonnenförmige Verzeichnung. Dann wird ein Quadrat mit nach außen gewölbten Seiten abgebildet, sieht also etwa wie eine Tonne aus (Name). Den umgekehrten Fall nennt man kissenförmige Verzeichnung. Dann sieht das Quadrat aus wie ein Sofakissen. Es kann auch wellenförmige Verzeichnung auftreten, wenn sich verschiedene Ordnungen der Verzeichnung überlagern. Gerade Linien werden dann wie Wellenlinien nach beiden Seiten gekrümmt.

Weitwinkelobjektive in Retrofokus-Bauweise (Schnittweite größer als Brennweite) neigen zur tonnenförmigen Verzeichnung und Teleobjektive (Baulänge kleiner als Brennweite) zur kissenförmigen.

Sogenannte Fischaugen-Objektive weisen eine starke tonnenförmige Verzeichnung auf. Dies ist gewollt, um einerseits einen größeren Bildwinkel zu erreichen (180 Grad und mehr sind nur durch Verzeichnung möglich), und andererseits die Verzeichnung für die Bildgestaltung einzusetzen.

Bei Feldstechern (Ferngläsern) mit Weitwinkelokularen ist eine kissenförmige Verzeichnung ausdrücklich erwünscht, um beim Schwenken des Glases eine unangenehme Bewegung des Vordergrundes gegenüber dem Hintergrund zu vermeiden. Die physikalische Grundlage hierfür stellt die so genannte „Winkelbedingung“ dar, die bei Feldstechern erfüllt sein soll (im Unterschied zu der „Tangentenbedingung“ bei Fotoobjektiven).

Siehe auch

Kaustik (Optik)

Basierend auf einem Artikel in:

Wikipedia.de