Residuum (Statistik)

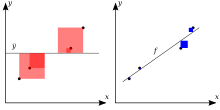
Die blauen Vierecke sind Residuenquadrate. Die roten Flächen bezeichnen die Gesamte Abweichungsquadratsumme.

In der Statistik bezeichnet man geschätzte Störgrößen als Residuen. Die Problematik bei der Regressionsdiagnostik ist, dass sich die Gauß-Markov-Annahmen auf die Störgrößen und nicht auf die Residuen beziehen. Die Summe der quadrierten Residuen spielt bei der Methode der kleinsten Quadrate eine große Rolle.

Gewöhnliche Residuen

In der einfachen linearen Regression sind die gewöhnlichen Residuen gegeben durch

${\hat {\varepsilon }}_{i}=y_{i}-{\hat {y}}_{i}=y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i}$ .

Hierbei handelt es sich um Residuen, da vom wahren Wert ein geschätzter Wert abgezogen wird. Genauer gesagt wird von der wahren Gerade $y_{i}$ die geschätzte Gerade ${\hat {y}}_{i}$ abgezogen. Da die Störgröße $\varepsilon_i$ offensichtlich vom einem wahren Wert $y_{i}$ als auch von einem geschätzten Wert ${\hat {y}}_{i}$ abhängt, wird ihr der "Hut aufgesetzt" und sie wird somit zum Residuum. Man unterscheidet somit wie folgt:

$\varepsilon_i$ : Unbeobachtbare zufällige Fehler bzw. Störgrößen, deren Existenz man annimmt
${\hat {\varepsilon }}_{i}=y_{i}-{\hat {y}}_{i}$ : Geschätzte Störgrößen bzw. Residuen

Da die Residuen im Gegensatz zu den Störgrößen beobachtbar und berechnete Größen sind, können sie graphisch dargestellt oder auf andere Weise untersucht werden. Im Gegensatz zur einfachen linearen Regression, bei der eine Gerade bestimmt wird, bestimmt man bei der multiplen linearen Regression (Erweiterung der einfachen linearen Regression auf Regressoren) eine Hyperebene, die durch die Punktwolke verläuft. Falls zwei Regressoren vorliegen, liegen die Beobachtungen bildlich gesprochen über beziehungsweise unter der Regressionsebene. Die Differenzen der beobachteten und der prognostizierten, auf der Hyperebene liegenden y-Werte, stellen die Residuen dar. Für sie gilt:

${\hat {\varepsilon }}_{i}=y_{i}-{\hat {y}}_{i}=y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i1}-{\hat {\beta }}_{2}x_{i2}-\dotsc -{\hat {\beta }}_{p}x_{ip}$ .

Die gewöhnlichen Residuen, die durch die Kleinste-Quadrate-Schätzung gewonnen werden sind, wenn zusätzlich n Beobachtungen vorliegen, in der multiplen linearen Regression gegeben durch

${\hat {\boldsymbol {\varepsilon }}}=\mathbf {y} -{\hat {\mathbf {y} }}=\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}}=\left(\mathbf {I} -\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\right)\mathbf {y} =(\mathbf {I} -\mathbf {P} )\mathbf {y}$ ,

wobei $\mathbf {Q} :=(\mathbf {I} -\mathbf {P} )$ eine Projektionmatrix oder genauer gesagt die symmetrische und idempotente Residualmatrix darstellt und ${\hat {\boldsymbol {\beta }}}=(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y}$ den KQ-Schätzer im multiplen Fall darstellt.

Eigenschaften

Die gewöhnlichen Residuen ergeben im Mittel 0, d. h.

$\operatorname {E} ({\boldsymbol {\hat {\varepsilon }}})=\mathbf {0}$ .

Die Kovarianzmatrix der gewöhnlichen Residuen ist gegeben durch

$\operatorname {Cov} ({\boldsymbol {\hat {\varepsilon }}})=\operatorname {Cov} (\mathbf {Q} \mathbf {y} )=\mathbf {Q} \operatorname {Cov} (\mathbf {y} )\mathbf {Q} ^{\top }=\mathbf {Q} \operatorname {Cov} ({\boldsymbol {\varepsilon }})\mathbf {Q} =\operatorname {Cov} ({\boldsymbol {\varepsilon }})\mathbf {Q} \mathbf {Q} =\sigma ^{2}\mathbf {Q} =\sigma ^{2}(\mathbf {I} -\mathbf {P} )$ .

Die gewöhnlichen Residuen sind heteroskedastisch, da

$\operatorname {Cov} ({\boldsymbol {\hat {\varepsilon }}})=\sigma ^{2}(\mathbf {I} -\mathbf {P} )=\sigma ^{2}\mathbf {Q} \neq \sigma ^{2}\mathbf {I}$ .

Dies impliziert, dass für die gewöhnlichen Residuen die Gauß-Markov-Annahmen nicht erfüllt sind.

Mithilfe einer Projektionsmatrix lässt sich zeigen, dass die Residuen mit den prognostizierten Werten unkorreliert sind

${\boldsymbol {\hat {\varepsilon }}}^{\top }{\hat {\mathbf {y} }}=\left(\left(\mathbf {I} -{\boldsymbol {P}}\right)\mathbf {y} \right)^{\top }{\boldsymbol {P}}\mathbf {y} =\mathbf {y} ^{\top }\left(\mathbf {I} -{\boldsymbol {P}}\right){\boldsymbol {P}}\mathbf {y} =\mathbf {y} ^{\top }\left({\boldsymbol {P}}-{\boldsymbol {P}}\right)\mathbf {y} =\mathbf {0}$ .

Residualvarianz

Die Varianz der Residuen (auch Resdualvarianz genannt) ist in der einfachen lineare Regression gegeben durch

$s_{u}^{2}={\frac {1}{n}}\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}={\frac {1}{n}}\sum \limits _{i=1}^{n}\left(y_{i}-b_{0}-b_{1}x_{i}\right)^{2}$ .

Partielle Residuen

Partielle Residuen-Streudiagramme werden mithilfe von partiellen Residuen erstellt, die definiert sind durch

${\hat {\varepsilon }}_{x_{j},i}:=y_{i}-{\hat {\beta }}_{1}-{\hat {\beta }}_{2}x_{i2}-\ldots -{\hat {\beta }}_{j-1}x_{i,j-1}\;{\hat {\beta }}_{j+1}x_{i,j+1}-\ldots -{\hat {\beta }}_{k}x_{i,k}=\mathbf {x} _{t}^{\top }{\hat {\boldsymbol {\beta }}}+{\hat {\beta }}_{j}x_{ij}$ .

Studentisierte Residuen

Für dieses einfache Modell sei die Design-Matrix

$\mathbf {X} ={\begin{pmatrix}1&x_{1}\\\vdots &\vdots \\1&x_{n}\end{pmatrix}}$

und die Prädiktionsmatrix $\mathbf{P}$ ist die Matrix der Orthogonalprojektion auf den Spaltenraum der Designmatrix. $\mathbf{P}$ ist gegeben durch

$\mathbf {P} =\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }$ .

Die statistischen Hebelwerte $p_{ii}$ sind die -ten Diagonalelemente der Prädiktionsmatrix. Die Varianz des -ten Residuums ist gegeben durch

$\operatorname {Var} ({\widehat {\varepsilon }}_{i})=\sigma ^{2}(1-p_{ii})$ .

In diesem Fall hat die Designmatrix ${\mathbf {X}}$ nur zwei Spalten, was zu folgender Varianz führt

$\operatorname {Var} ({\widehat {\varepsilon }}_{i})=\sigma ^{2}\left(1-{\frac {1}{n}}-{\frac {(x_{i}-{\overline {x}})^{2}}{\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}\right)$ .

Die dazugehörigen studentisierten Residuen sind dann

$t_{i}={{\widehat {\varepsilon }}_{i} \over {\widehat {\sigma }}{\sqrt {1-p_{ii}\ }}}$ .

Die studentisierten Residuen sind identisch (aber nicht unabhängig) verteilt und damit insbesondere homoskedastisch. Sie könnten somit eine Lösung für die Verletzung der Homoskedastizitätsannahme darstellen.

Basierend auf einem Artikel in:

Wikipedia.de